
- •Колледж министерства иностранных дел российской федерации
- •Кафедра специальных и общепрофессиональных дисциплин
- •Математика
- •Оглавление
- •1. Определение непрерывности функции
- •2. Непрерывность элементарных функций
- •1. Определение производной
- •2. Геометрический смысл производной
- •3. Физический смысл производной
- •1. Понятие первообразной функции
- •2. Неопределенный интеграл.
Министерство иностранных дел Российской Федерации
Колледж министерства иностранных дел российской федерации
(ФБУ СПО Колледж МИД России)
Кафедра специальных и общепрофессиональных дисциплин
Цикловая комиссия по информатике
Математика
Реферат на тему: Основные понятия математического анализа
Выполнила: Харьковская Е.С.
Группа:22
Преподаватель: Колганова Н.И.
Москва - выпуск 2012
Оглавление
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ 4
ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИЙ 4
НЕПРЕРЫВНОСТЬ ФУНКЦИИ 6
1. ОПРЕДЕЛЕНИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ 6
2. НЕПРЕРЫВНОСТЬ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 6
ПРОИЗВОДНАЯ ФУНКЦИИ 6
1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ 6
2. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ 7
3. ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ 8
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 9
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ 9
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ 11
ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ 11
ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ И ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 11
ПОНЯТИЕ ПРОИЗВОДНОЙ N-ГО ПОРЯДКА 13
ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ. 13
ОТЫСКАНИЕ ТОЧЕК ЛОКАЛЬНОГО ЭКСТРЕМУМА ФУНКЦИИ 14
НАПРАВЛЕНИЕ ВЫПУКЛОСТИ И ТОЧКИ ПЕРЕГИБА ГРАФИКА ФУНКЦИИ 16
СХЕМА ИССЛЕДОВАНИЯ ГРАФИКА ФУНКЦИИ 17
ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 17
1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ 18
2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. 18
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ 19
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
Определение.
Число А называется пределом функции
f(x) в точке
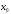 (или при
(или при
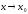 ),
если для любого числа
),
если для любого числа
 >0
существует такое, что для всех х,
принадлежащих Х,
>0
существует такое, что для всех х,
принадлежащих Х,
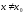 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
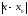 <
<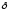 ,
выполняется неравенство
,
выполняется неравенство
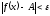 .
.
Символически
это записывается так:
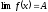 .
.
ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИЙ
Теорема 1. Пусть функции f(х) и g(х) имеют в точке пределы В и С. Тогда функция f(x) ± g(x) имеет в точке х0 предел, равный В + С, т.е.
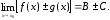
Теорема
2. Пусть
функции f(x)
и g(x) имеют
в точке х0 пределы В и С. Тогда
функция
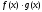 имеет в точке х0 предел, равный
имеет в точке х0 предел, равный
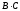 ,
т.е.
,
т.е.
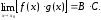

Следствие. Постоянный множитель можно выносить за знак предела, т.е.
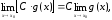
где f(x) = C – постоянный множитель.
В самом деле,
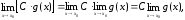
так как

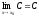 (см. пример 1 п.1.).
(см. пример 1 п.1.).
Теорема
3. Пусть
функции f(x)
и g(x) имеют
в точке х0 пределы В и С. Тогда
функция
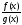 (при С≠0) имеет в точке х0 предел,
равный
(при С≠0) имеет в точке х0 предел,
равный
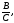 т.е.
т.е.
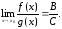
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
1. Определение непрерывности функции
Пусть на
некотором промежутке
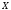 определена
функция
определена
функция
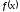 и точка
и точка
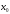 принадлежит этому промежутку.
принадлежит этому промежутку.
Определение.
Функция
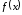 называется непрерывной в точке
называется непрерывной в точке
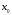 ,
если предел функции и ее значение в этой
точке равны, т.е.
,
если предел функции и ее значение в этой
точке равны, т.е.

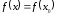
2. Непрерывность элементарных функций
Все функции, получаемые с помощью конечного числа арифметических действий над простейшими элементарными функциями, а также суперпозицией этих функций, составляют класс элементарных функций.
Теорема
2.4. Пусть функции
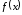 и
и
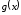 непрерывны в точке
непрерывны в точке
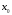 .
Тогда функции
.
Тогда функции
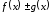 ,
,
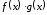 и
и
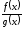 также непрерывны в этой точке (последняя
при
также непрерывны в этой точке (последняя
при
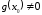 ).
).
ПРОИЗВОДНАЯ ФУНКЦИИ
1. Определение производной
Пусть на
некотором промежутке X
определена функция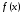 .
Возьмём любую точку
.
Возьмём любую точку
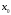 из X и придадим аргументу
x в точке
из X и придадим аргументу
x в точке
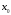 произвольное приращение
произвольное приращение
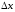 такое,
что точка
такое,
что точка
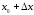 также
будет принадлежать X.
Функция получит приращение
также
будет принадлежать X.
Функция получит приращение
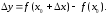
Определение.
Производной функции
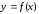 в точке
в точке
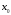 называется предел при
называется предел при
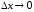 отношение приращения функции в этой
точке к приращению аргумента (при
условии, что этот предел существует).
отношение приращения функции в этой
точке к приращению аргумента (при
условии, что этот предел существует).
Символически это записывается так:
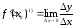
или
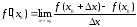 ,
,
или,
вспоминая, что
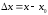 и
и
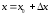 ,
,
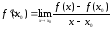 .
.
