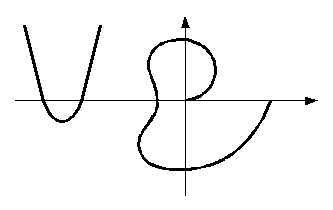экзамен / tau.pottee
.doc|
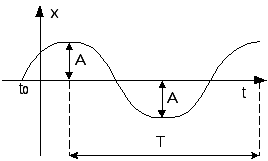
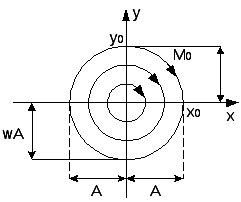
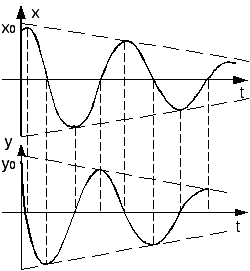
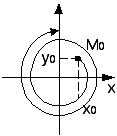
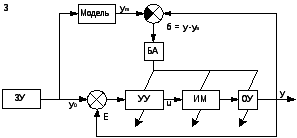
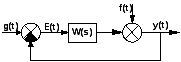
1. Понятие системы автоматического управления, принципы управления, класс-ция САУ. Управление - организаця того или иного процесса на основе имеющейся информации, которая направлена на достижение определенной цели. ОУ (Объект управления) характеризуется входными (управляющими) координатами, а также переменными состояния.
Этапы замкнутого процесса управления:
Цель управления – В каждый момент времени вектор выходных координат y должен быть равен заданному вектору y0: y → y0 при t→∞ Принципы управления:
|
Классификация САУ:
По соотношению начальной и рабочей информации: обычные, адаптивные
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
2. Уравнения динамических звеньев их линеаризация. При составлении дифференциальных уравнений динамики любой автоматической системы ее разбивают на отдельные звенья и записывают уравнения каждого звена в отдельности. Уравнение должно быть составлено так, чтобы оно выражало зависимость между входными и выходными величинами для этого звена. Динамическое уравнение составляется по правилам соответствующей технической науки. У звена может быть несколько входных величин, а также внешнее воздействие.
Линеаризация:
|
1. Аналитический способ Разложим функцию F, стоящую в левой части в ряд Тейлора по степеням малых отклонений.
Вычитая из (5) (2) перйдем к уравнению в отклонениях:
Это уравнение приближенное, т.к. отброшенымалые высокого порядка. Переменные не x,y, а их отклонения - ∆x, ∆y. Это уравнение линейное относительно ∆x, ∆y с постоянными коэффициентами.
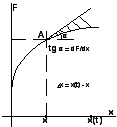
2. Геометрический способ Заключается в том, что криволинейные зависимости заменяются прямолинейными (по касательной в соответствующей точке кривой) |
|||||||||||||||||||||||||||||||||||||||||||||||
|
3. Расчет свободных и вынужденных процессов в линейных САУ
Типовые входные воздействия
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
4. Временные характеристики динамических звеньев.
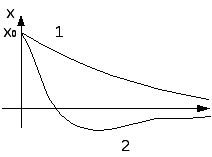
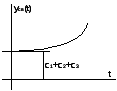
Временные характеристики определяют вид изменения выходного сигнала при подаче на вход звена типового управляющего воздействия. Это позволяет сравнивать свойства звеньев в динамических режимах работы. Временные свойства звена определяются его переходной и импульсной переходной характеристиками. Переходная
функция или переходная характеристика
h(t)
представляет собой переходный процесс
на выходе звена, возникающий при подаче
на его вход скачкообразного воздействия
при величине скачка, равного единице.
Такое воздействие называется единичной
ступенчатой функцией и обозначается
X(t)=1(t),
что соответствует следующим условиям(0):
Изображение единичной ступенчатой
функции определяется как
Чтобы
определить изображение переходной
функции при известной передаточной
функции звена W(s)
необходимо выполнить следующую
операцию:
Уравнение линейного динамического звена имеет следующий общий вид(1):
где
|
Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу
Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов(2)
Получим из (2) отношение изображений
выходного и входного сигналов (3).
Отношение изображений выходного и
входного сигналов называют передаточной
функцией дин. звена
Функция веса или импульсная переходная
характеристика представляет собой
реакцию звена на единичную импульсную
функцию. Единичная импульсная функция,
или δ– функция, представляет собой
производную от единичной ступенчатой
функции. То есть
Дельта-функция тождественно равна
нулю во всех точках, кроме t=0, где она
стремится к бесконечности. Нетрудно
установить, что изображение дельта-функции
определяется как
Изображение функции веса определяется
как:
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
5. Прямое и обратное преобразование Лапласа Трудности исследования САУ с помощью аппарата дифуров привели к тому что в инженерной практике используются методы основаные на преобразовании Лапласа. Основное достоинство такого преобразования – замена операций интегрирования, дифференцирования на алгебраические действия по отношению к изображению.
|
6. Свойства преобразования Лапласа Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. Свойства преобразования Лапласа существенно облегчают задачу нахождения изображений для большого числа разнообразных функций, а также задачу отыскания оригиналов по их изображениям.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
7. Частотные характеристики динамических звеньев.
Частотные характеристики звена
определяют его реакцию на гармонический
входной сигнал в установившемся режиме
(т.е. после завершения переходных
процессов). Частотной характеристикой
динамического звена называют функцию
комплексного аргумента jw, полученную
путем формальной замены s на jw в
выражении передаточной функции
Получим связь частотной характеристики
с известными понятиями. Для этого
рассмотрим динамическое звено с
передаточной функцией W(s) и сигналами,
Получим отношение спектров
Таким образом, частотную характеристику динамического звена можно определить как отношение спектра (преобразования Фурье) выходного сигнала к спектру входного сигнала. Знание частотной характеристики звена позволяет определить выходной спектр по входному
Рассмотрим динамическое звено –
Получим спектр выходного сигнала –
импульсной характеристики
|
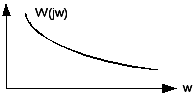
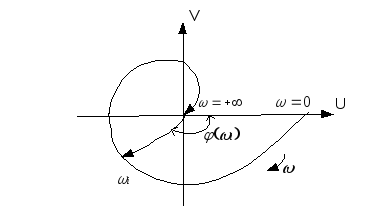
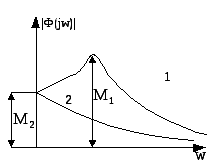
Для динамического звена с передаточной функцией W(s) в общем случае различают следующие частотные характеристики: а) амплитудно-фазовая характеристика (АФХ) – это график частотной передаточной функции W(jw), построенная на комплексной плоскости(1) Графическое изображение АФХ на комплексной плоскости называется годографом.
б) амплитудно-частотная характеристика (АЧХ) звена определяется отношением амплитуд выходного и входного сигналов на частоте w=2πf(2) в) фазо-частотная характеристика (ФЧХ) определяет сдвиг по фазе между выходным и входным сигналами (3) г) логарифмическая амплитудно-частотная характеристика (ЛАХ) – это АЧХ звена, построенная в логарифмических шкалах(4) д) логарифмическая фазо-частотная характеристика (ЛФХ) – имеет логарифмический масштаб только по оси частот. Построение ЛАХ типового динамического звена, как правило, сводится к построению асимптотической ЛАХ, представляющей собой совокупность отрезков прямых с наклоном, кратным 20 дб\дек. Физический смысл АЧХ и ФЧХ: 1) показывает, как изменяется протекание сигнала различной частоты, при этом оценка пропускания делается по соотношению амплитуд входных и выходных величин; 2) показывает фазовые сдвиги, вносимые звеном на различных частотах.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
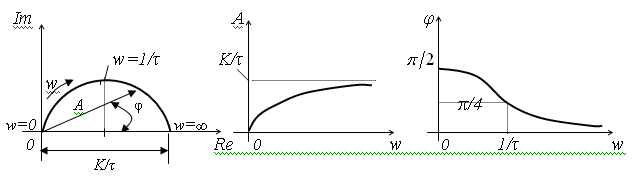
8. Апериодическое (инерционное) звено первого порядка.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
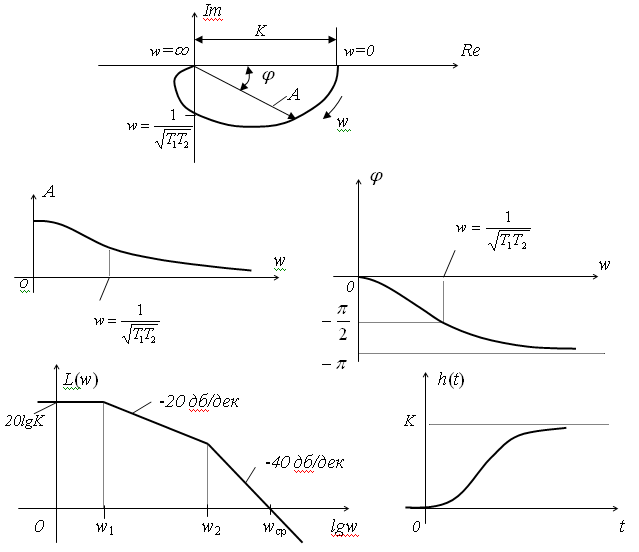
9. Апериодическое звено второго порядка.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
10. Колебательное звено второго порядка.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
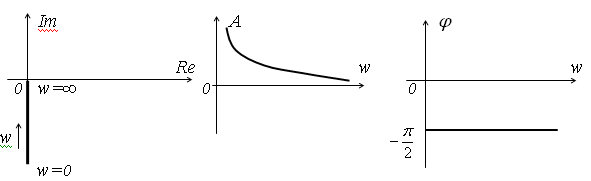
11. Интегрирующие звенья и их характеристики. Идеальное интегрирующее звено.
Изодромное звено (пропорционально-интегрирующее звено).
Это звено имеет передаточную функцию
Таким образом, изодромное звено может быть также представлено как последовательное соединение интегрирующего и форсирующего звеньев. |
12. Инерционно-форсирующее (реальное форсирующее) звено.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
13. Дифференцирующие звенья и их характеристики. Идеальное дифференцирующее звено.
|
Реальное дифференцирующее звено.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
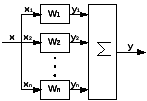
14. Соединения звеньев, передаточные функции соединений звеньев Все разнообразие соединений можно осуществить 3 способами.
|
15.Передаточные функции замкнутой САУ
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
16. Понятие устойчивости линейной системы. Необходимый критерий устойчивости.
|
17. Алгебраические критерии устойчивости Гурвица
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
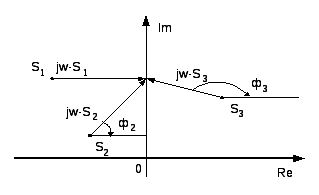
18. Принцип аргумента. В основе всех частотных критериев устойчивости лежит принцип аргумента.
|
∆arg(jw-Si)= +П (7)
∆arg(jw-Si)= -П (8)
Допустим что характеристическое
уравнение вида
Имеет m правых корней, l левых корней. l+m=n ∆arg D(jw)=П(l-m)=П(n-2m) (9) (Принцип аргумента)
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
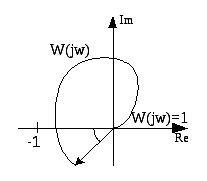
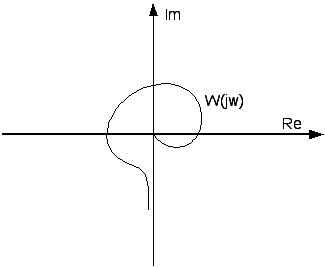
19. Частотный критерий устойчивости Найквиста.
1-устойчива, 2-неусточива. Замкнутая система устойчива, если на охватывает точку с координатами (-1, j0)
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
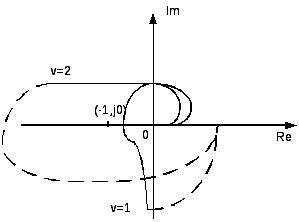
20. Частотный критерий устойчивости Найквиста. (2)
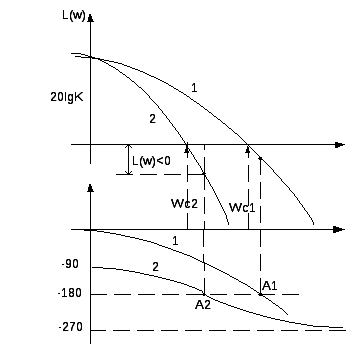
САУ нейтральная в разомкнутом состоянии устойчива, если годограф разомкнутой системы с его дополнением бесконечности не охватывает точку (-1,j0) Определение устойчивости системы с помощью логарифмических частотных характеристик.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
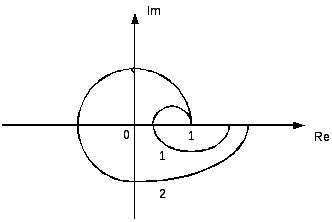
21. Критерий устойчивости Михайлова.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
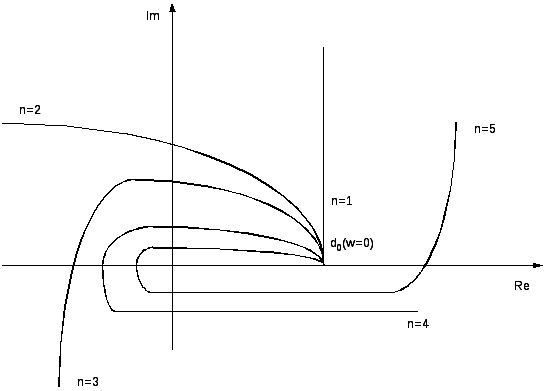
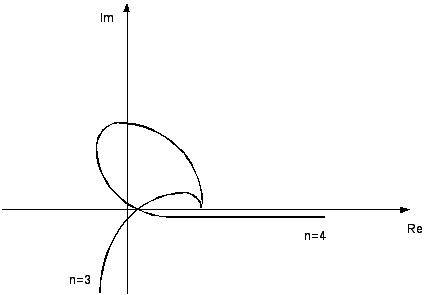
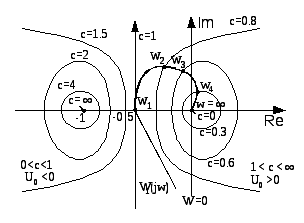
22. Построение областей устойчивости системы методом Д-разбиения.
Штриховка: При движении от 0 до ∞ штриховка производится слева (для случая с одним параметом). |
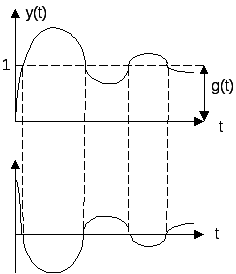
23. Прямые показатели качества САУ Оцениваются непосредственно по переходному процессу системы.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
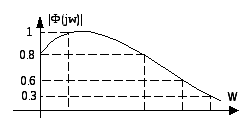
24. Частотные показатели качества САУ
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
25. Корневые показатели качества САУ
где
Переходный процесс зависит как от
полюсов, так и от нулей, то есть
определяется как левой, так и правой
частями дифференциального уравнения.
Это существенно усложняет анализ.
Поэтому рассмотрим частный, но весьма
распространенный случай, когда
передаточная функция замкнутой САУ
не имеет нулей:
Тогда уравнение динамики приобретает
вид:
Общее решение данного уравнения имеет
вид:
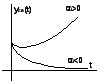
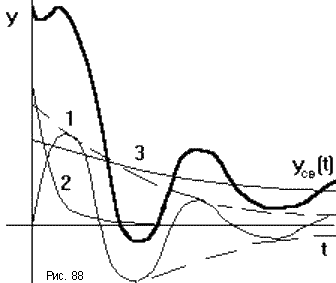
Время пер. процесса tПП опр. длительностью своб. процесса, который предст. собой сумму n экспоненциально затухающих сост-х (рис.88). Затухание каждой из сост-х опр. вещественной частью соотв. плюса pi, которая для устойчивых систем должна быть отриц. Длительность переходного процесса определяется в основном свободной составляющей, имеющей наименьшее затухание, то есть наименьшее абсолютное значение вещественной части соответствующего полюса.
|
По степени устойч. h можно прибл. вычислить время перех. процесса, которое опр. по моменту, когда свобо. составляющая с наименьшим затуханием уменьшится до величины Δ*Ai , где Ai – нач. зн. данной сост-ей:
В общем случае, когда передаточная функция замкнутой САУ имеет нули, то использование данного метода может дать большую ошибку. Однако всегда качество управления будет тем лучше, чем больше h и меньше m, поэтому данный метод имеет смысл для любых САУ, но приближенно.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
26. Интегральные оценки качества САУ Инт. критерии позв. судить о качестве упр. путем вычисления интегралов от нек. функций управляемой величины. Эта функция выбирается таким путем, чтобы значение определенного интеграла от этой функции по времени от 0 до +∞ было однозначно связано с кач. перех. процесса. В то же время данный интеграл должен сравн. просто выч. ч/з коэффициенты ур-ий исслед. системы.
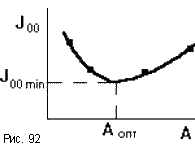
Чем она меньше, тем выше быстродействие
системы. При выборе параметров системы
стремятся обеспечить мин. Joo. Если
имеется какой-то варьируемый параметр
A, то можно построить кривую Joo = f(A)
(рис.92). Ее минимум, опр. из условия
dJoo/dA = 0, даст опт. зн. A. Пусть дано ур-е
динамики замкн. САУ: |
Пусть при t = 0 САУ имела следующие начальные условия:
так как процесс затухает и при t-->∞ свободная составляющая и все производные становятся равны нулю. Подставляя эти значение, получаем:
То есть линейную оценку качества регулирования можно легко вычислить, зная начальные условия и коэффициенты дифференциального уравнения. Возможны и другие линейные оценки качества, но они используются реже, например:
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
27. Интегральные оценки качества САУ (2)
При выборе параметров САУ по минимуму
J20 часто получают
нежелательную колебательность
процесса, так как приближение yсв(t)
к оси ординат вызывает резкое увеличение
начальной скорости, что в свою очередь
может вызвать большое перерегулирование,
уменьшив при этом запас устойчивости.
Для того, чтобы обеспечить плавность
протекания процесса, в квадратичную
оценку качества добавляется слагаемое,
зависящее от скорости изменения
регулируемого параметра yсв’(t).
Получаем критерий качества
Где - некоторая наперед заданная постоянная времени, определяющая весовое соотношение между оценкой по yсв и по yсв’. При малых значениях уменьшение колебательности будет незначительным. Завышение увеличит время переходного процесса так, что ее выбор определяется конкретными условиями. |
Задача выбора параметров САУ по минимуму J20 и J21 решается аналитически только в случае невысокого порядка дифференциального уравнения. Иначе используют ЭВМ.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
28. Статическая точность САУ Точность систем управления при отработке ступенчатого сигнала
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
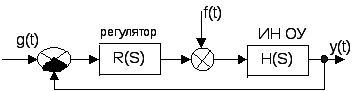
29. Метод коэффициентов ошибок. Рассматриваемый метод может применяться как для задающего g(t), так и для возмущающего f(t) воздействий. Рассм. случай, когда имеется только задающее воздействие. Если функция времени g(t) имеет произвольную форму, но достаточно плавную вдали от начальной точки процесса в том смысле, что через нек. время существенное знач. имеет только конеч. число m производных
то ошибку системы можно опр. след. образом.
где Фх(р) – передаточная функция замкнутой системы по ошибке, G(p) изображение задающего воздействия. Разложим передаточную функцию по ошибке в ряд по возрастающим степеням компл. величины р:
сходящийся при малых значениях р, т.е. при достаточно больших значениях времени t, что соответствует установившемуся процессу изменения управляемой величины при заданной форме задающего воздействия. Переходя к оригиналу, получаем формулу для установившейся ошибки
Величины с0, с1, с2, … называются коэффициентами ошибок. Они могут определяться согласно общему правилу разложения функции в ряд Тейлора по формулам
|
Так как передаточная функция по ошибке представляет собой дробно-рациональную функцию, то коэффициенты ошибок можно более просто получить делением числителя на знаменатель и сравнением получающегося ряда с выражением (*). Коэффициент с0 может быть отличным от нуля только в статических системах и не только в тех случаях, когда не принимаются меры по устранению первой составляющей статической ошибки посредством масштабирования или использования нееденичных обратных связей. В системах с астатизмом первого порядка с0=0, а коэффициент с1 связан с добротностью по скорости соотношением с1=1/К. В системах с астатизмом второго порядка с0=0 и с1=0, а коэффициент с2 связан с добротностью по ускорению соотношением с2/2=1/К. При исследовании ошибки от возмущающегося воздействия можно получить все коэффициенты не равными нулю при астатизме любого порядка, так как астатизму по задающему воздействию может соответствовать наличие статической ошибки по возмущению. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
30. Понятие астатизма. Способы повышения устойчивости САУ. При одном и том же типовом воздействии точность установившегося движения различных систем может сильно отличаться друг от друга, если отличаются коэффициенты ошибок систем. Это положено в основу классификации систем по порядку астатизма. Системой с нулевым порядком астатизма по задающему воздействию g(t) (стат. системой), наз-ся такая система, установившаяся ошибка которой при отработке постоянного воздействия g(t)=a0*1[1] пропорциональна величине этого воздействия.
Из формулы
Системой с астатизмом 1-го порядка
(астат. системой) наз-ся точная система,
установившаяся ошибка которой равна
0 при постоянном воздействии, а при
отработке воздействие линейно
изменяется во времени.g(t)=a0+a1(t)
постоянна и пропорциональна скорости
изменения, отсюда c0=0,
Системой с астатизмом v-го
порядка называется система, установившаяся
ошибка которой при отработке воздействия
Порядок астатизма системы равен номеру первого, отличного от нуля коэффициенту ошибки. Корневыми оценками называются такие, которые основываются на расположении характеристического уравнения замкнутой системы, а также нулей замкнутой передаточной функции.
Степень устойчивости представляет
собой расстояние
|
В общем случае замкнутая передаточная система имеет вид:
Нули замкнутой передаточной функции оказывают существенное влияние на характер переходного процесса, могут ухудшать или улучшать его качество. Наиболее целесообразным с практ. точки зрения является размещение нулей передаточной функции системы вблизи ее полюсов.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
31. Задача синтеза САУ. Виды корректирующих устройств. Под синтезом САУ понимается задача выбора и расчета специальных корректирующих устройств, обеспечивающих заданные статические и динамические св-ва. Синтез САУ: структурный, параметрический. При синтезе предполагается, что в основные ф-ые элементы исполн. и измерит. уже выбраны в соответствии с ТЗ и составляют вместе с объектом управления неизменяемую часть системы. К изменяемой части относятся коррект. устройства, определяемые в результате синтеза.
Виды корректирующих устройств. Последовательные корр. уст-ва
2. Увеличение общего к-та усиления разомкнутой системы
|
Параллельные корректирующие устройства
1. Жесткая обратная связь Wку(S) = K Wоу(S) = K/(ToS+1) ПОС(+) ООС(-)
Если К↑ то вместо Wоу(S) поставим Ko/S W(S) = K1/(T1S+1), K1=1/K↓ T1=1/(K0K)↓ при К↑ |
|||||||||||||||||||||||||||||||||||||||||||||||
|
32. Задача синтеза САУ. Виды корректирующих устройств. (2) 2. Инерционная жесткая обратная связь.
3. Гибкая обратная связь Wky(S) = KS
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
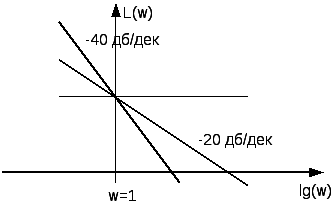
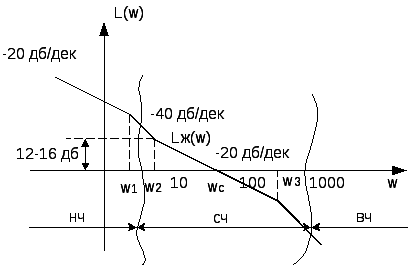
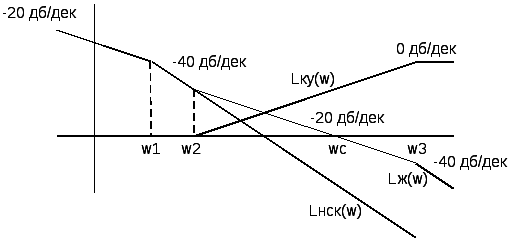
33. Синтез САУ методом ЛАХ.
Если перегиб однократный λ = 1 -20→ -40 [дб/дек]
|
Если перегиб двукратный λ = 2 -20→ -60 [дб/дек]
В ВЧ динамич. параметры не учитывают.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
34. Синтез САУ аналитическим методом. Метод модального управления. Метод модального управления – аналитический метод синтеза ли-
нейных САУ. Указанный метод обеспечивает
заданное распределение полюсов
передаточных функций замкнутой САУ
на комплексной плоскости. Естественно,
возможность решения указанной задачи
зависит от степени наблюдаемости и
управляемости САУ (строгие опеделения
наблюдаемости и управляемости выходят
за рамки этого курса). Постановка
задачи. Пусть имеется ОУ, заданный
в форме уравнений состояния.
Требуется найти управление u=
CTX,
где вектор управления
1. Задаемся характеристическим полиномом
замкнутой САУ (полином знаменателя),
т.е. задаем желаемое расположение его
корней
2. Опр. характеристический полином
разомкн. САУ.
3. Из коэффициентов полиномов D(s)
и d(s)
сформируем вектор
4. Найдем искомый вектор управления
Пример синтеза линейной САУ Пусть
задан объект управления с помощью
передаточной функции вида
|
Характерно, что метод мод. управления абсолютно не учитывает статические свойства САУ. Поэтому зачастую необходимо проводить коррекцию статической ошибки регулирования до применения метода мод. упр., а после процедуры синтеза необходимо осуществлять проверку стат. свойств САУ. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
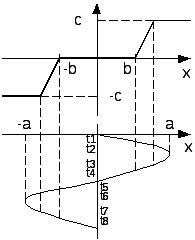
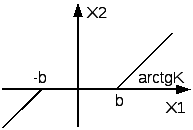
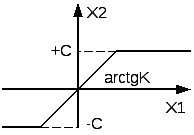
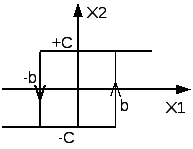
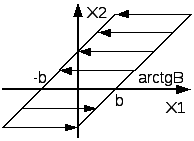
35. Понятие о нелинейных системах. Виды нелинейностей.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
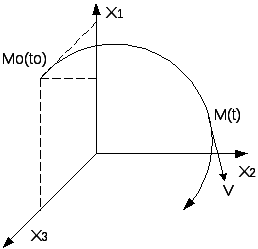
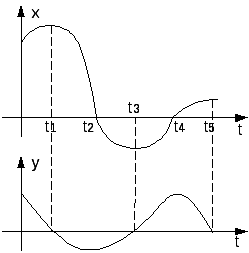
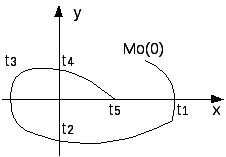
36. Фазовое пространство и фазовая плоскость. Метод фазового пространства
Точки равновесного состояния системы называют особыми точками на фазовой плоскости.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
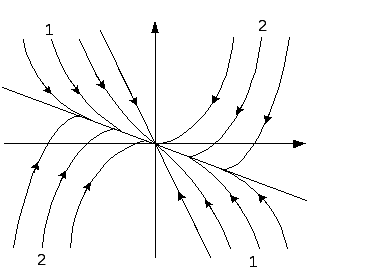
37. Виды фазовых портретов линейных систем второго порядка.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
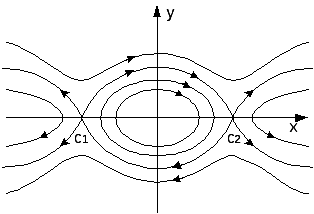
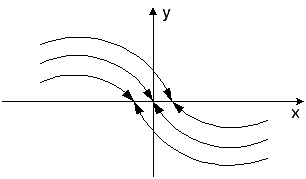
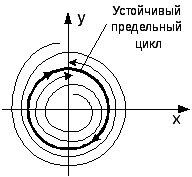
38. Особенности фазовых портретов нелинейных систем.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
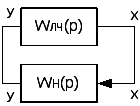
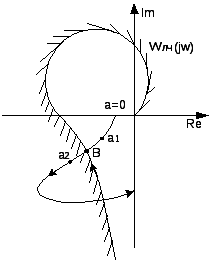
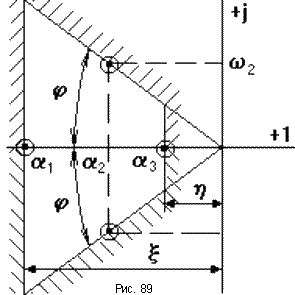
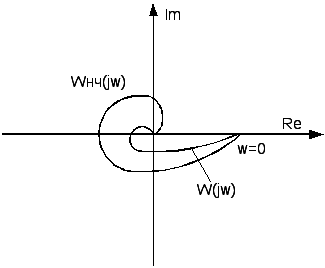
39.Частотный критерий абсолютной устойчивости нелинейных систем В.М. Попова.
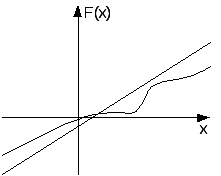
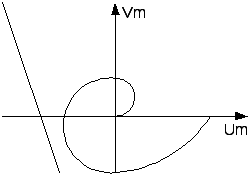
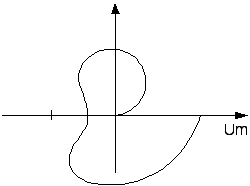
Графическая интерпретация. 1.Состояние равновесия нелинейной системы абсолютно устойчиво, если нелинейная характеристика F(x) находится внутри сектора [0,kmax] и можно привести через точку (-1/kmax,0) прямую таким образом, что она не пересечет модифицированную частотную характеристику вида: Wм(jw)=Uлч(w)+jwVлч(w)
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
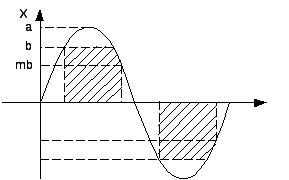
40. Метод гармонической линеаризации.
Такой период. выходной сигнал нелинейного звена можно разложить в ряд Фурье.
В основе метода гармонической линеаризации лежит представление некоторой линейной периодической ф-ии в виде (2). При этом во внимание берутся лишь первые гармоники.
|
Гипотеза фильтра. При наличии свойства фильтра лин.часть системы должна хорошо пропускать первую гармонику нелинейных колебаний и ослабляет все высшие гармоники.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
41. Вычисление коэффициентов гармонической линеаризации.
|
42. Определение автоколебаний в нелинейной системе методом Гольдфарба.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||



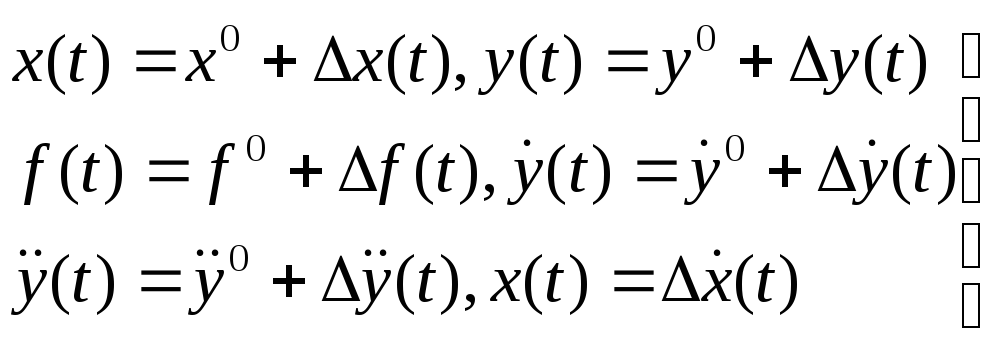
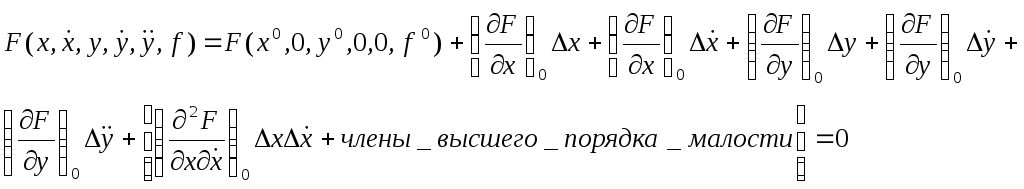
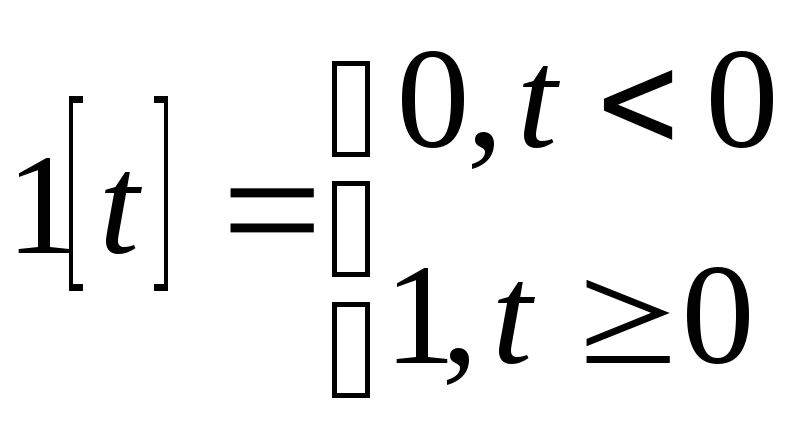
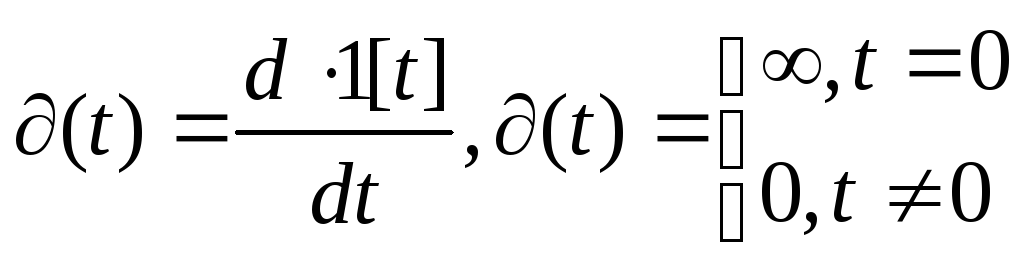
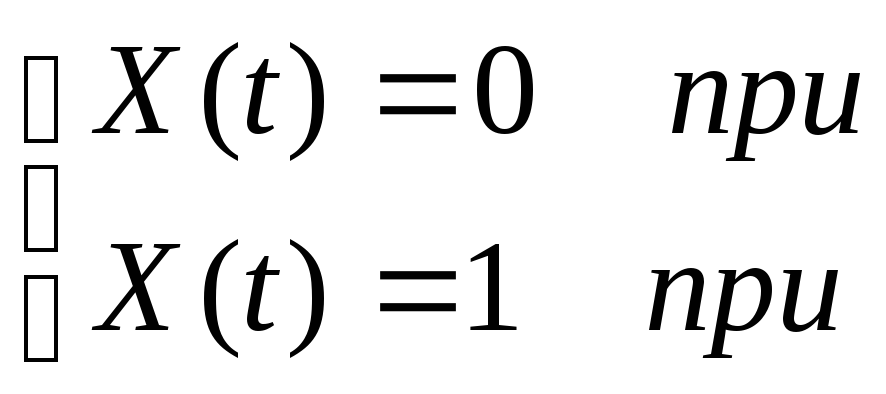
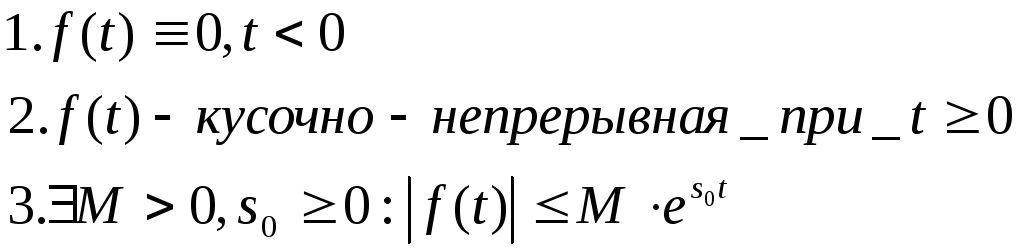
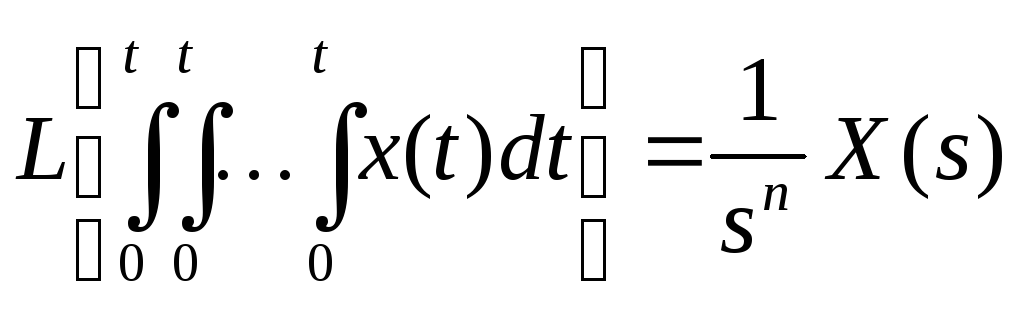

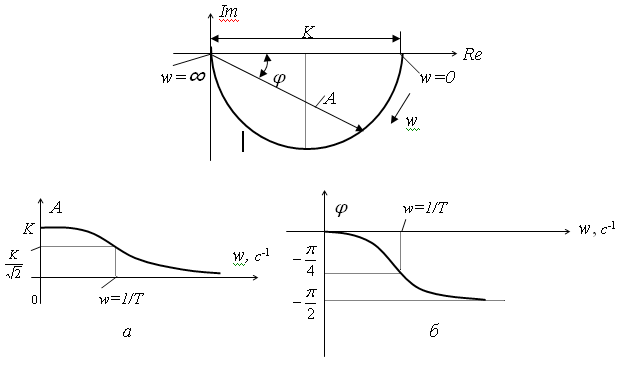

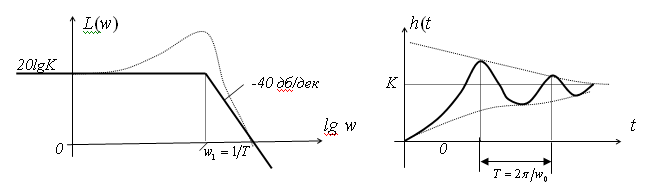
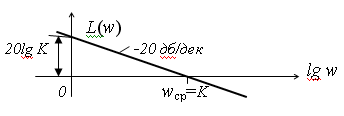

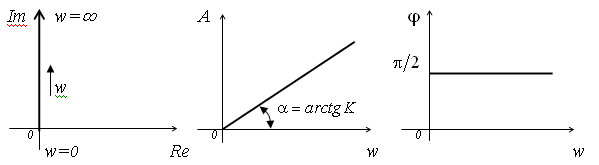
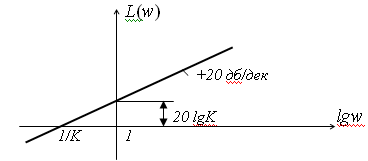



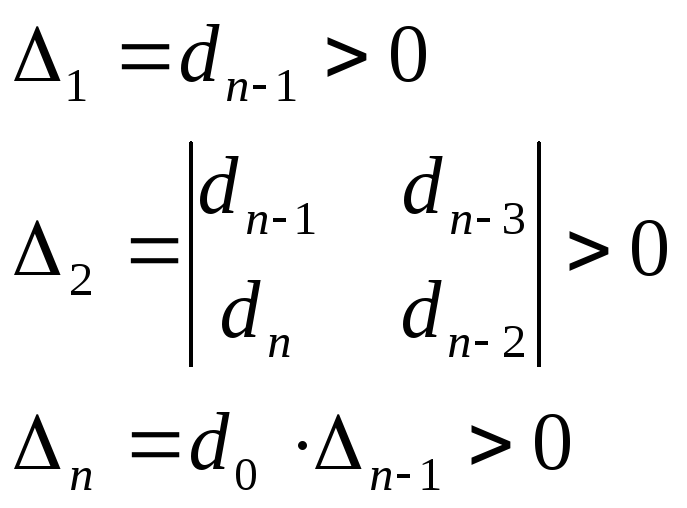


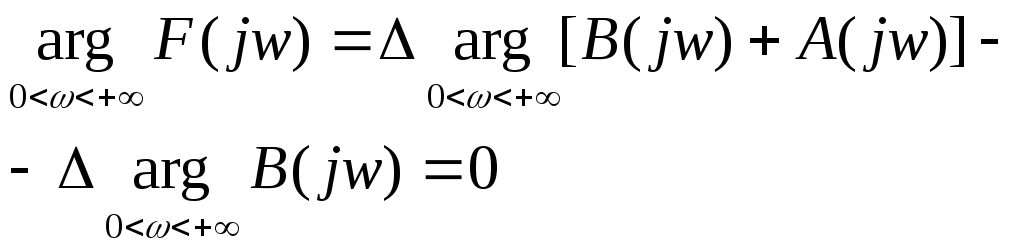
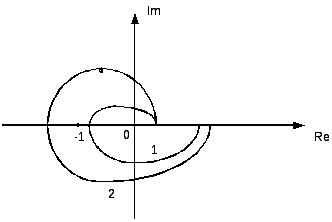
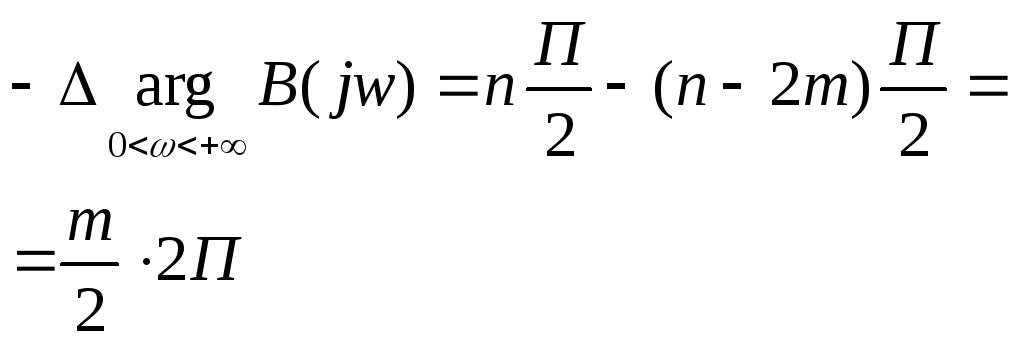 САУ
устойчива, если при изменении W
от 0 до ∞, годограф разомкнутой
системы W(jw)
охватывает m/2 раз точку
(-1,j0) в положительном
направлении.
САУ
устойчива, если при изменении W
от 0 до ∞, годограф разомкнутой
системы W(jw)
охватывает m/2 раз точку
(-1,j0) в положительном
направлении.






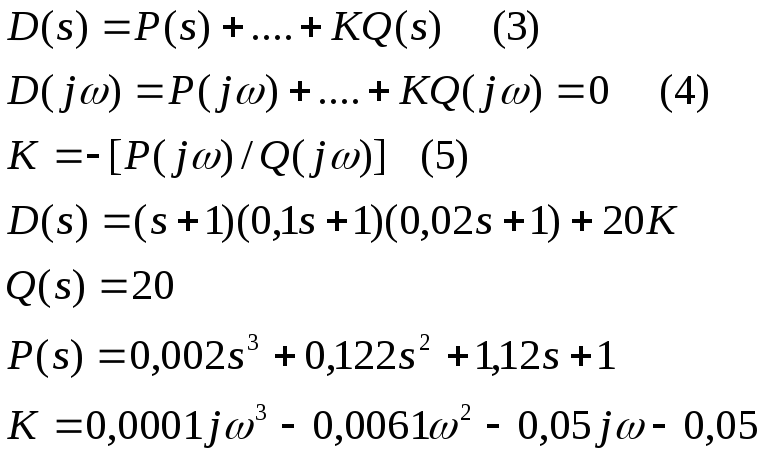
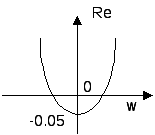
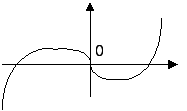 ImK=0.0001w(w2-0.056)
ImK=0.0001w(w2-0.056)
 (4)
(4)


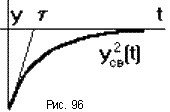
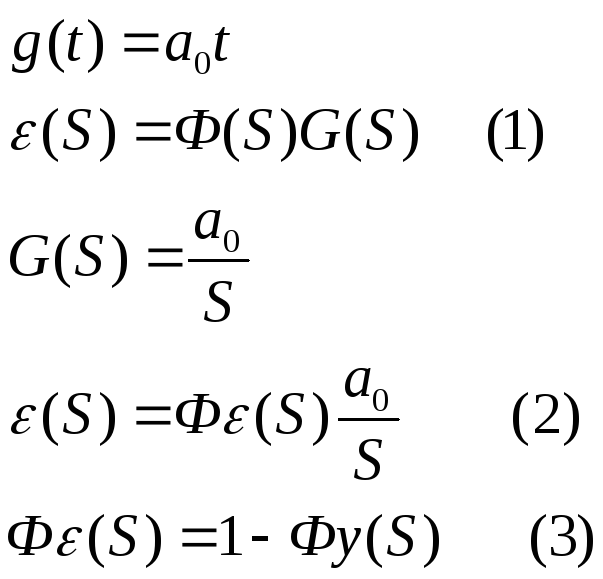
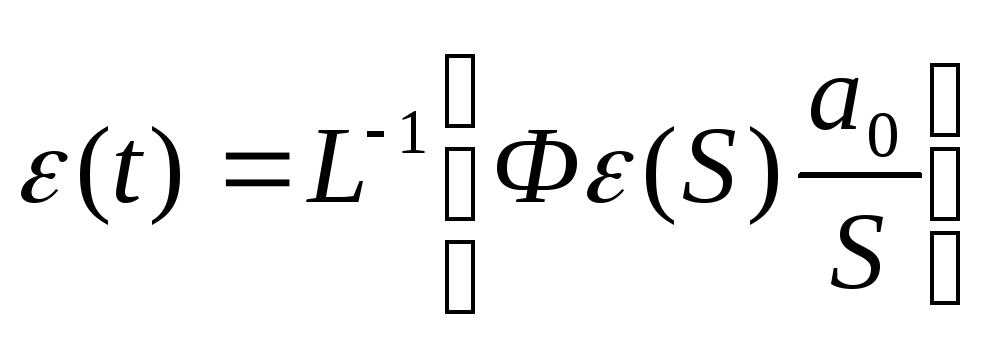


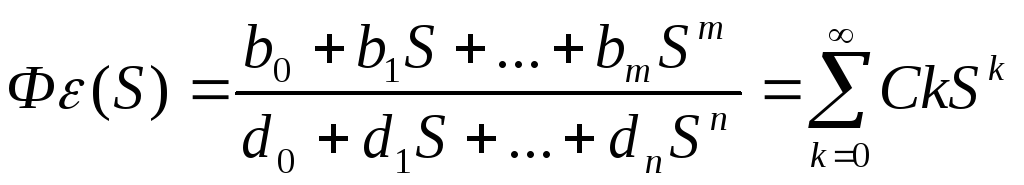 при
s->∞
при
s->∞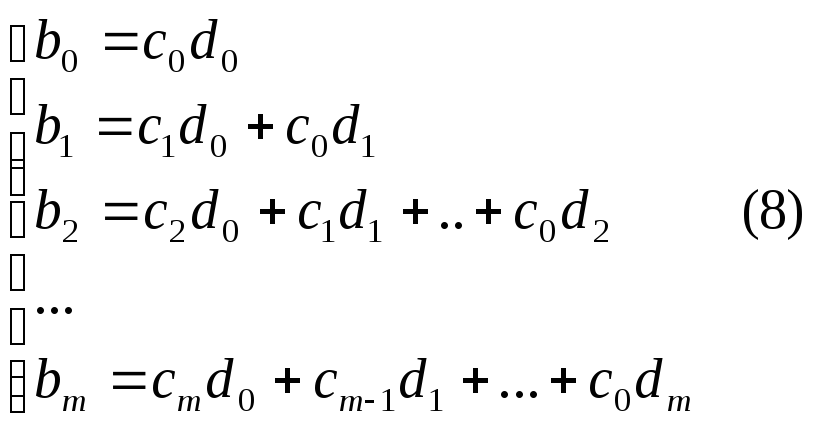
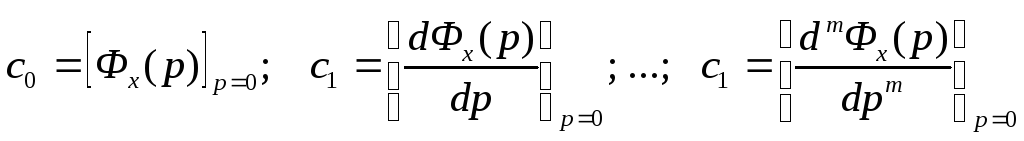
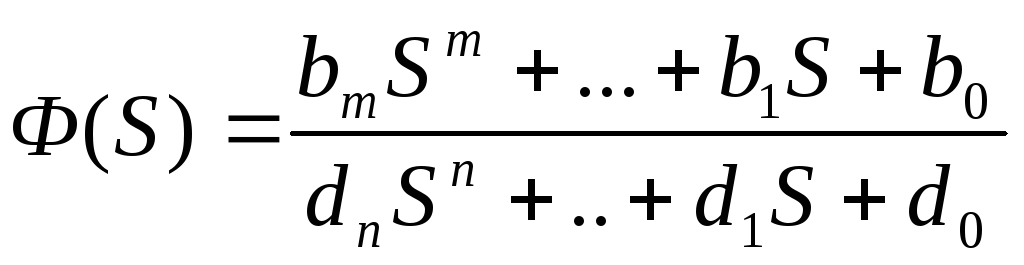

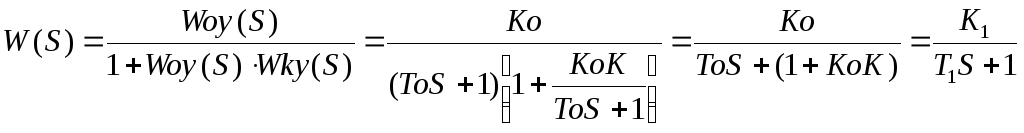
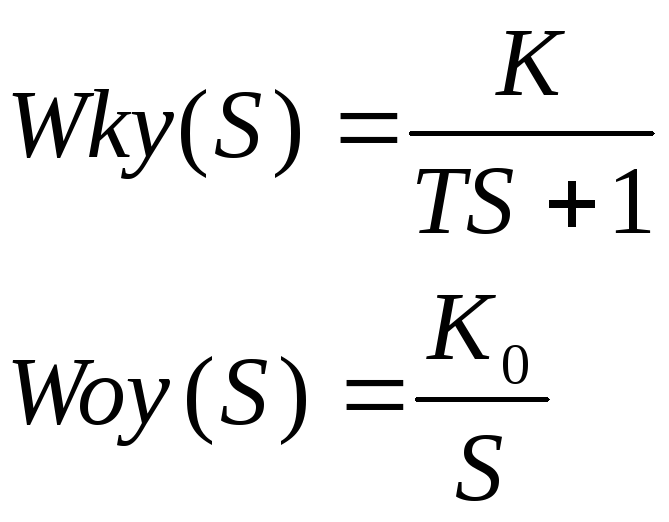 ООС
(-)
ООС
(-)
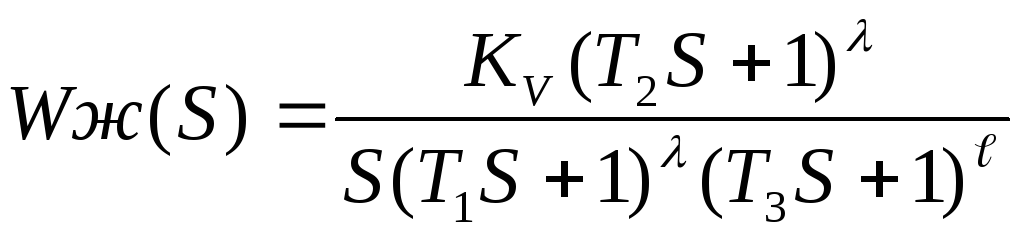

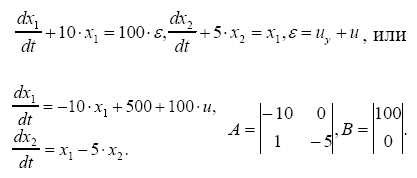
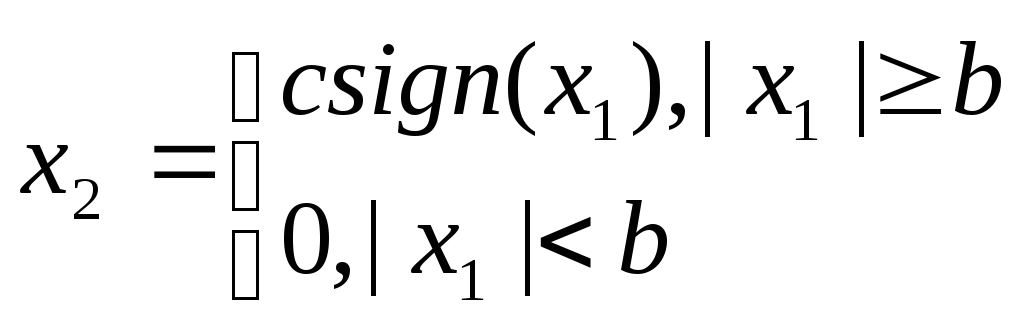
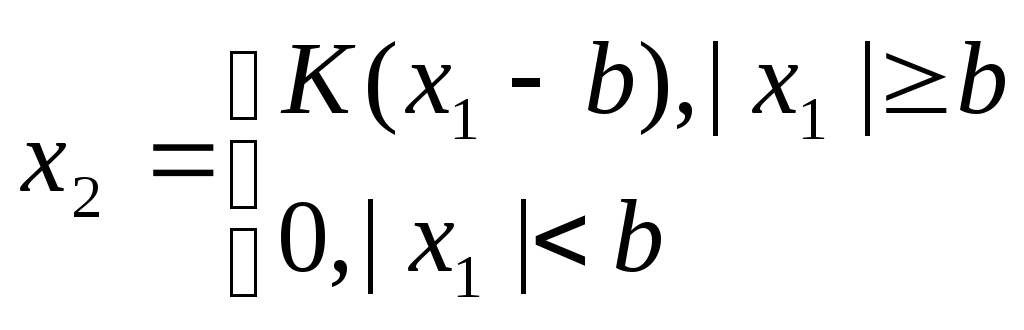
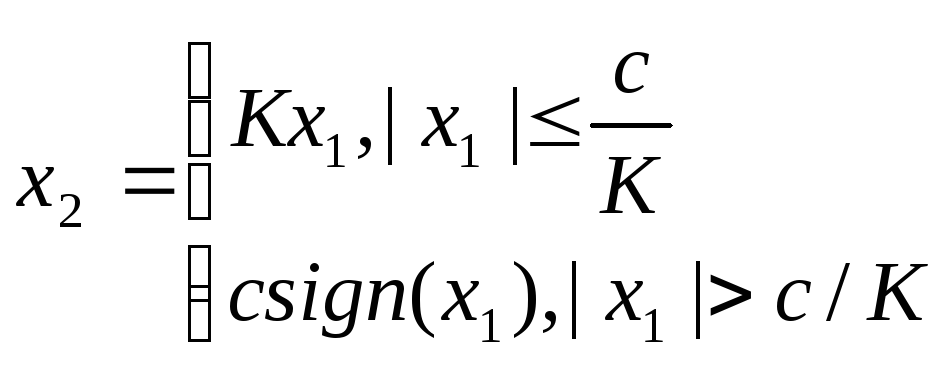
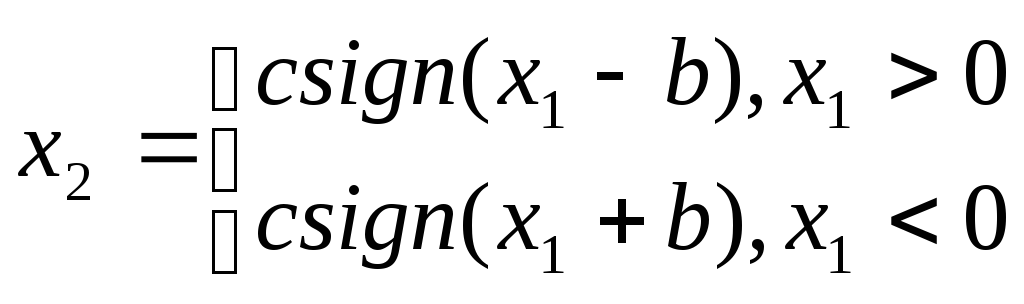

 -->
-->
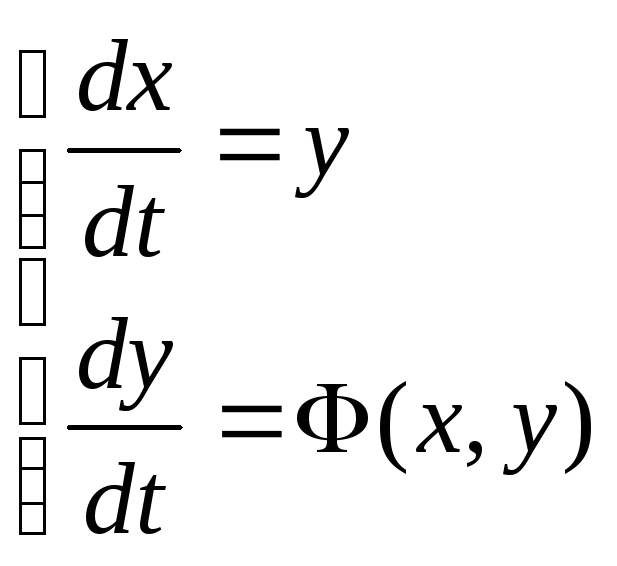

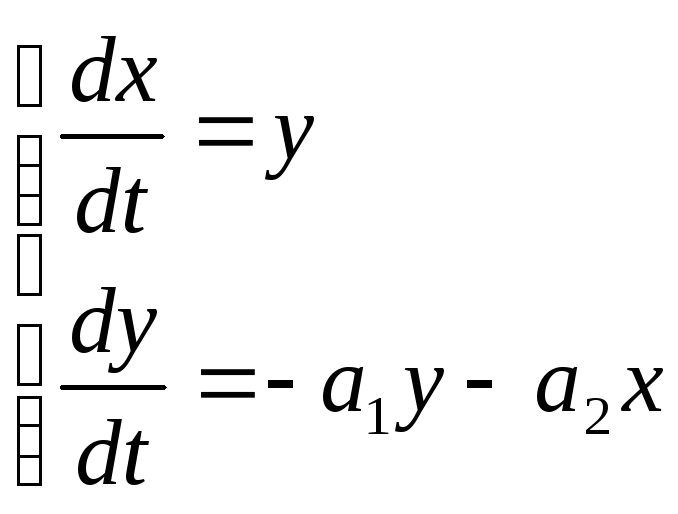 (2)
(2)