Содержание

Введение 2

1 Определение передаточной функции звена 3

2 Определение переходной функции звена 4

3 Определение весовой функции звена 4

4 Определение КЧХ звена 5

5 Определение ВЧХ и МЧХ звена 6

6 Структурная схема САР 9

7 Передаточная функция замкнутой системы 11

8 Передаточная функция разомкнутой системы 11

9 Определение устойчивости системы 13

Теоретические вопросы 14

Список использованных источников 18

Дано дифференциальное уравнение звена

.

Необходимо:

1. Определить передаточную функцию звена.

2. Определить переходную функцию звена .

3. . Определить весовую функцию звена .

4. . Определить КЧХ звена.

5. Определить АЧХ и ФЧХ звена.

Решение:

1 Определим передаточную функцию, если известно дифференциальное уравнение.

Для этого вынесем за скобки y(t).

Передаточная функция системы – отношение изображения по Лапласу её выходного сигнала к изображению по Лапласу её входного сигнала при нулевых начальных условиях.

Тогда

2 Определим переходную функция звена:

Переходная характеристика ­– это реакция системы на единичное ступенчатое воздействие (скачок).

Для определения переходной функции в Маткаде воспользуемся панелью инструментов Symbolic:

3 Определим весовую функцию звена (весовая или импульсная переходная характеристика – это реакция системы на единичный импульс.):

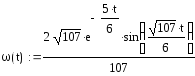
Частотной характеристикой линейной системы или, что эквивалентно, комплексной частотной функцией линейной системы называется функция W(i), получаемая из передаточной функции системы при подстановке p=i. {КЧХ объекта широко используются при анализе систем управления на устойчивость, а также при расчетах параметров настройки регуляторов.4

4 Определим КЧХ звена

Построим амплитудно – фазочастотную характеристику (годограф) звена.

Вычислим последовательно комплексные числа, далее – функцию Re (вещественная часть) и Im (мнимая часть) и таким образом получим:

Далее построим годограф звена.

5 Определим АЧХ и ФЧХ звена:

Вещественная частотная характеристика:

Мнимая частотная характеристика:

Амплитудная частотная характеристика есть модуль комплексного числа. Исходя из этого, найдем АЧХ звена:

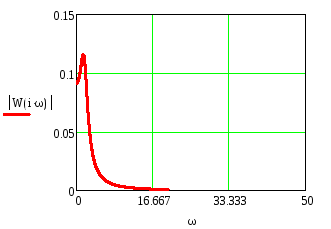
Фазо- частотная характеристика есть аргумент комплексного числа. Исходя из этого, найдем ФЧХ звена.

Таким образом, получены частотные характеристики звена, а также весовая и переходная функции.

2 Дана структурная схема замкнутой САР

где:

T – 0,1;

Т₁ – 6;

ξ – 0,01;

К – 3,1.

Необходимо:

1. Записать передаточную функцию разомкнутой системы.

2. Записать передаточную функцию замкнутой системы.

3. Определить, является ли данная система устойчивой (по критерию Найквиста). Известно, что данная система в разомкнутом состоянии является устойчивой.