2.2 Рівняння еліптичного типу
Якщо
рівняння (1.1) є рівнянням еліптичного
типу, то існують такі функції
та
,
що
і дане рівняння зводиться до канонічної
форми
. (2.18)
Опишемо процедуру знаходження цих функцій.
Спочатку формально, як і у попередньому випадку, приводимо рівняння (1.1) до вигляду
(2.19)
При
цьому нові змінні
та
будуть комплексно спряженими
,
, (2.20)
оскільки диференціальні рівняння характеристик (2.15) та (2.16) у випадку, що розглядається, мають вигляд
, 
. (2.21)
Таким чином, рівняння еліптичного типу має лише уявні характеристики.
Виконаємо нову заміну змінних
,
, (2.22)
внаслідок якої рівняння (2.19), а отже і рівняння (1.1) зводиться до шуканої канонічної форми з точністю до зміни позначень
.
Приклад
2.3 Звести
до канонічного вигляду рівняння
Розв’язування
Для визначення типу рівняння складемо його дискримінант. Оскільки
,
то дане рівняння є рівнянням еліптичного
типу.
Диференціальні рівняння характеристик та їх загальні інтеграли такі:
1)
;
;
,
звідси
;
2)
;
,
звідси
.
Отримані змінні комплексні, тому згідно з (2.22) знаходимо остаточну заміну змінних
,
.
Згідно з (2.4) маємо
,
.
Підставимо знайдені похідні у наше рівняння, маємо
,
.
2.3 Рівняння параболічного типу
Якщо
рівняння (1.1) є рівнянням параболічного
типу, то функції
та
підбираються такі, що
,
і дане рівняння зводиться до канонічної
форми
. (2.23)
Опишемо процедуру знаходження цих функцій.
Знаходимо
функцію
,
яка є розв’язком рівняння
(2.24)
Як і
у випадку гіперболічного рівняння
припускаємо, що
та розв’яжемо рівняння (2.24) відносно
.
При цьому отримуємо лише одне рівняння
характеристик
, (2.25)
оскільки
.
Нехай
є загальний інтеграл рівняння (2.25),
звідки
.
Інша змінна
вибирається довільним чином за умови,
що
і
перетворює на нуль коефіцієнт
.
Приклад
2.4
Звести до канонічного вигляду рівняння
.
Розв’язування
Для визначення типу рівняння складемо його дискримінант. Оскільки
,
то дане рівняння є рівнянням параболічного
типу.
Складемо згідно з (2.25) диференціальне рівняння характеристик
,
,
звідки
.
Рівняння
для другої незалежної змінної можна
взяти у вигляді
,
оскільки за такого вибору якобіан
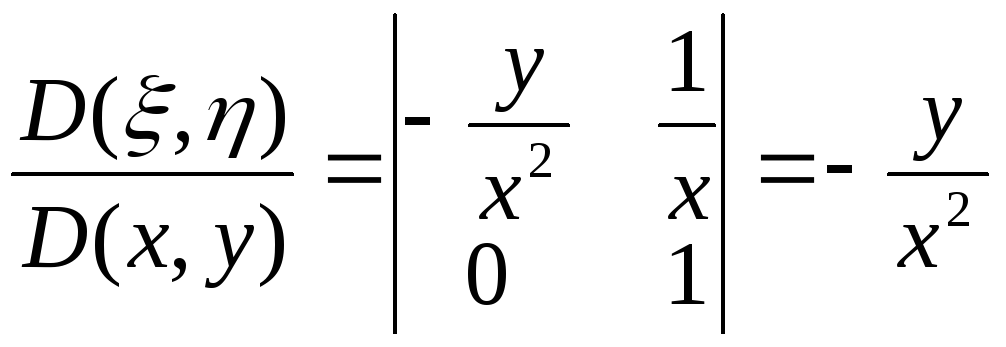
відмінний
від нуля в усіх точках площини
,
крім точок осі
і згідно з (2.7) перетворює на нуль
коефіцієнт
.
Згідно з (2.4) маємо
;
;
.
Підставимо знайдені похідні у наше рівняння, маємо
.
Розглянемо декілька прикладів на зведення рівнянь до канонічного вигляду в системі аналітичних обчислень Maple
Зауваження:
В системі Maple
визначник старших коефіцієнтів
обчислюється за формулою
-
рівняння параболічного типу
-
рівняння еліптичного типу
-
рівняння гіперболічного типу.
Приклад 2.5 Звести до канонічного вигляду рівняння
.
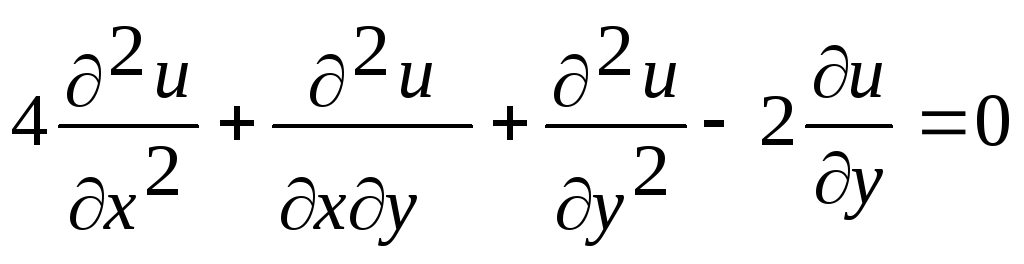