Розв’язування
Розв’язуємо задачу в системі аналітичних обчислень Maple. Задаємо рівняння
> a[1]:= 4;a[2]:=4;a[3]:=1;a[4]:=0;a[5]:=-2;a[6]:=0;a[7]:=0;
> equ:=a[1]*diff(u(x,y),x,x)+a[2]*(x,y diff(u(x,y),x,y)+ +a[3]*diff(u(x,y),y,y)+a[4]*diff(u(x,y),x)+a[5]*diff(u),y)+ +a[6]*u(x,y)+a[7]=0;
equ:=
> eq:=lhs(equ);
equ:=
Обчислюємо матрицю старших коефіцієнтів і її визначник
> A:= linalg[matrix](2,2,[coeff(eq,diff(u(x,y),x,x)), coeff(eq,diff(u(x,y),x,y))/2, coeff(eq,diff(u(x,y),x,y))/2, coeff(eq,diff(u(x,y),y,y))]);
> Delta:=simplify(linalg[det](A));
Оскільки
визначник матриці старших коефіцієнтів
,
то тип рівняння – параболічний.
Формуємо характеристичне рівняння і розв’язуємо його.
> A[1,1]*z^2-2*A[1,2]*z+A[2,2]=0;res1:=solve(A[1,1]*z^2-2*A[1,2]*z+A[2,2],z);
> subs(y=(x),res1[1]);res2:=dsolve(diff(y(x),x)=%,y(x));
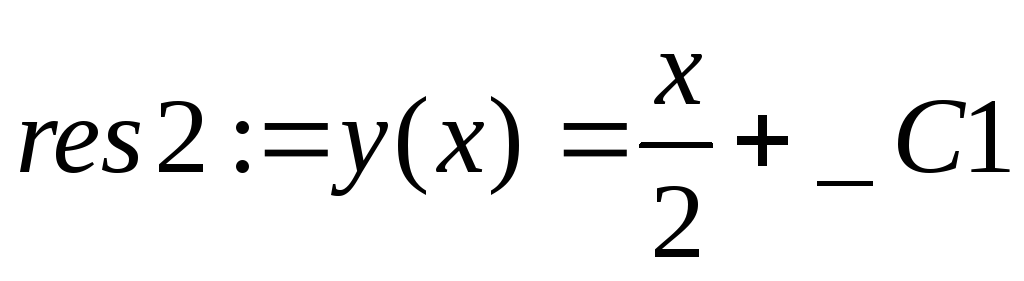
Одержали одне сімейство характеристик. Вводимо заміну змінних.
> res2:=subs(y(x)=y,res2);
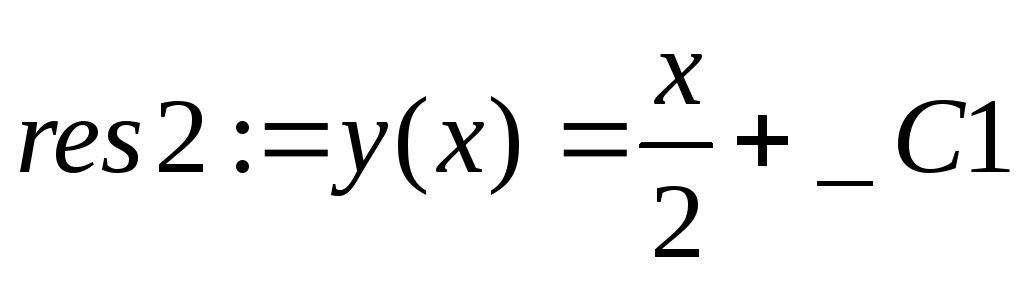
> itr:={xi=solve(res2,_C1),eta=y};
itr:=
Зводимо задане рівняння до канонічного вигляду
> tr:=solve(itr,{x,y}); PDEtools[dchange](tr,eq,itr,[eta,xi],simplify)=0;
tr:=
Зауваження: Якщо вибрати другу заміну змінних
> itr:={xi=solve(res2,_C1),eta=x};
itr:=
то одержимо рівняння виду:
> tr:=solve(itr,{x,y});
PDEtools[dchange](tr,eq,itr,[eta,xi],simplify)=0;
tr:=
Приклад 2.6 Звести до канонічного вигляду рівняння
Розв’язування
Розв’язуємо задачу в системі аналітичних обчислень Maple. Задаємо коефіцієнти нашого рівняння і саме рівняння
> a[1]:= 3;a[2]:=2;a[3]:=-1;a[4]:=2;a[5]:=3;a[6]:=0;a[7]:=0;
>equ:=a[1]*diff(u(x,y),x,x)+a[2]*diff(u(x,y),x,y)+a[3]*diff(u(x,y),y,y)+a[4]*diff(u(x,y),x)+ +a[5]*diff(u(x,y),y)+a[6]*u(x,y)+a[7]=0;
equ:=
> eq:=lhs(equ);
eq:=
Обчислюємо матрицю старших коефіцієнтів і її визначник
> A:= linalg[matrix](2,2,[coeff(eq,diff(u(x,y),x,x)), coeff(eq,diff(u(x,y),x,y))/2, coeff(eq, diff(u(x,y),x,y))/2, coeff(eq,diff(u(x,y),y,y))]);
> Delta:=simplify(linalg[det](A));
Оскільки
визначник матриці старших коефіцієнтів
,
то тип рівняння – гіперболічний.
Формуємо характеристичне рівняння і розв’язуємо його.
>A[1,1]*z^2-2*A[1,2]*z+A[2,2]=0;res1:=solve(A[1,1]*z^2-2*A[1, 2]*z+A[2,2],z);
> res2:={seq(dsolve(diff(y(x),x)=res1[i],y(x)),i=1..2)};
> res2:=subs(y(x)=y,res2);
Таким чином, ми одержали дві характеристики. Виконуємо заміну змінних.
> {seq(solve(res2[i],_C1),i=1..nops(res2))};
> itr:={xi=solve(res2[1],_C1),eta=solve(res2[2],_C1)};
Тепер зводимо задане рівняння до канонічного вигляду.
>tr:=solve(itr,{x,y});PDEtools[dchange](tr,eq,itr,[eta,xi], simplify)=0;
Приклад 2.7 Звести до канонічного вигляду рівняння
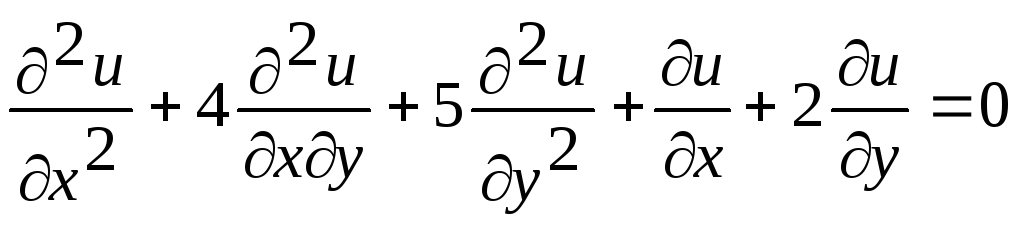
Розв’язування
Задаємо рівняння
> a[1]:=3;a[2]:=2;a[3]:=1;a[4]:=2;a[5]:=3;a[6]:=0;a[7]:=0;
>equ:=a[1]*diff(u(x,y),x,x)+a[2]*diff(u(x,y),x,y)+a[3]*diff(u(x,y),y,y)+[4]*diff(u(x,y),x)+ +a[5]*diff(u(x,y),y)+a[6]*u(x,y)+a[7]=0;
equ:=
> eq:=lhs(equ);
eq:=
Обчислюємо матрицю старших коефіцієнтів і її визначник
> A:= linalg[matrix](2,2,[coeff(eq,diff(u(x,y),x,x)), coeff(eq,diff(u(x,y),x,y))/2,coeff(eq, diff(u(x,y),x,y))/2, coeff(eq,diff(u(x,y),y,y))]);
> Delta:=simplify(linalg[det](A));
Оскільки
визначник матриці старших коефіцієнтів
,
то тип рівняння еліптичний.
Формуємо характеристичне рівняння і розв’язуємо його.
>A[1,1]*z^2-2*A[1,2]*z+A[2,2]=0;res1:=solve(A[1,1]*z^2-
–2*A[1, 2]*z+A[2,2],z);
> res2:={seq(dsolve(diff(y(x),x)=res1[i],y(x)),i=1..2)};
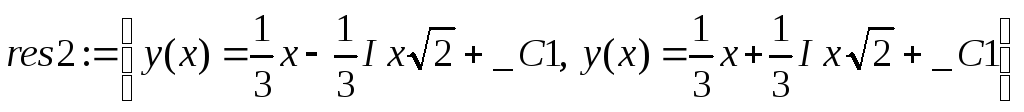
Таким чином, ми одержали дві комплексні характеристики. Виконаємо заміну змінних.
> res2:=subs(d(x)=d,res2);
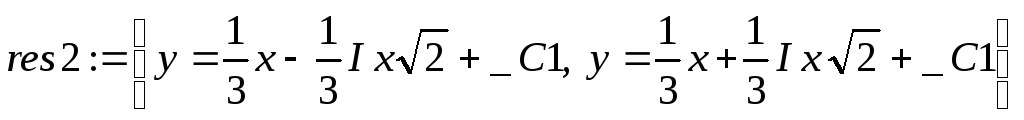
> {seq(solve(res2[i],_C1),i=1..nops(res2))};
> itr:= {xi=coeff(%[1],I),eta=%[1]-coeff(%[1],I)*I};
Тепер зводимо дане рівняння до канонічної форми
>tr:=solve(itr,{x,y});PDEtools[dchange](tr,eq,itr,[eta,xi], simplify)=0;
Приклад 2.8 Знайти загальний розв’язок рівняння зі сталими коефіцієнтами
