3. Еластичний шлях

Еластичний - це шлях, який буде проходити через одну вершину кожного етапу з мінімальним виробництвом коефіцієнтів жорсткості. Він і буде якраз максимально компенсувати початкове збурення в пропозиціях 1-5.

Таким чином, еластичний шлях визначає компенсуючі можливості системи. Створення коефіцієнтів жорсткості елементів, лежачих на цьому шляху є не чим іншим, як коефіцієнтом жосткості всієї системи в вказаних припущеннях.

Відзначимо, що еластичний шлях, отриманий в результаті вирішення однопродуктової задачі на мережі не залежить від величини недопоставки . Отже, можна розглядати довільну систему збурень, що йдуть на будь-які елементи системи. Від кожного такого збурення буде йти свій еластичний шлях в кінцеву вершину П.

Кожен із коефіцієнтів жорсткості, відповідний такому еластичному шляху, характеризує компенсуючі можливості системи по відношення до одного чи іншого збурення.

4. Розрахунок резервів для системи

Розглянемо, з чого складаються резерви простого ланцюга об’єктів, наприклад, представленого на рис.5.

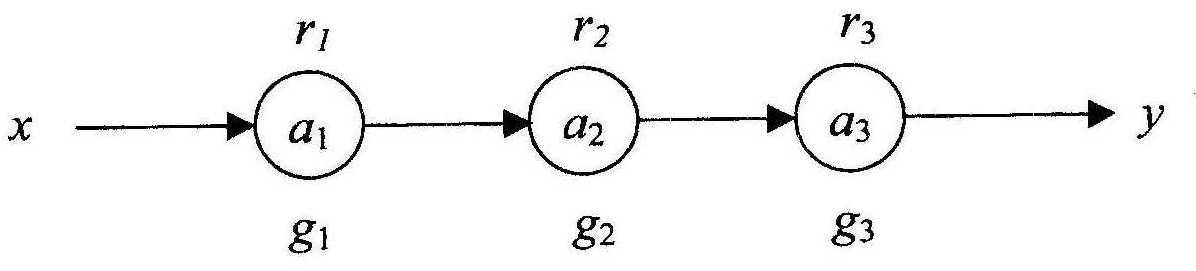
Рис. 4. Найпростіший ланцюг елементів

- резерв елемента ;

- коефіцієнт жорсткості функції еластичності елемента ;

x – вхідне збурення;

y – недовипуск продукції.

Можна побачити, що

Згідно з останньою формулою від вхідного збурення х поряд з резервом віднімається величина . Таким чином, всю величину можна інтерпретувати як повний резерв точки . Величину умовно можна називати непрямим резервом цієї точки першого роду, - непрямим резервом другого роду.

Для довільної послідовності довжиною L можна записати загальну формулу (8):

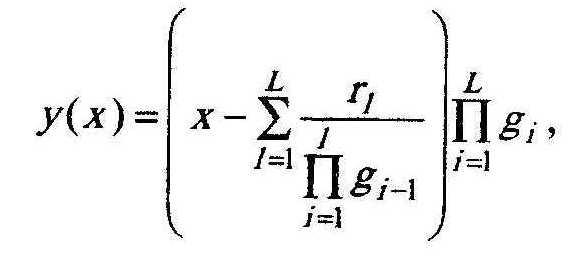
де

Формула для повного резерву першого об’єкта послідовності має вигляд: (9)

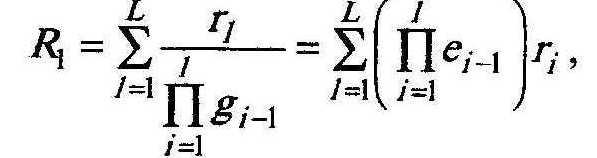
де - коефіцієнт еластичності.

В загальному випадку для вершини із якої виходять m ланцюжків, які починаються з , об’єктів, повний резерв складе: (10)

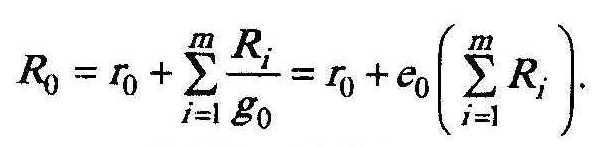
5. Багатокритеріальна задача розподілу збурень та алгоритм її розв’язання

Власне задача:

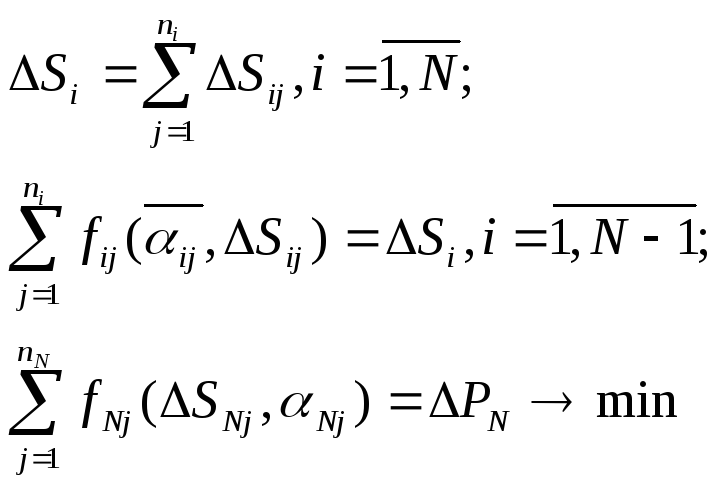
де, - функція еластичності j-того об’єкту, i-того етапу.

Алгоритм розв’язання:

1. Підраховуються повні резерви для всіх об’єктів (вершин) системи.

2. Розподіляється недопоставка по об’єктах першого етапу. Якщо власних резервів 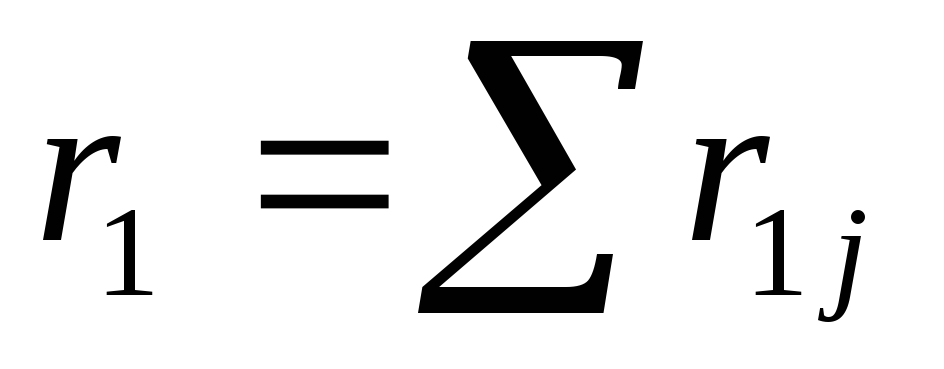достатньо для компенсації , оскільки 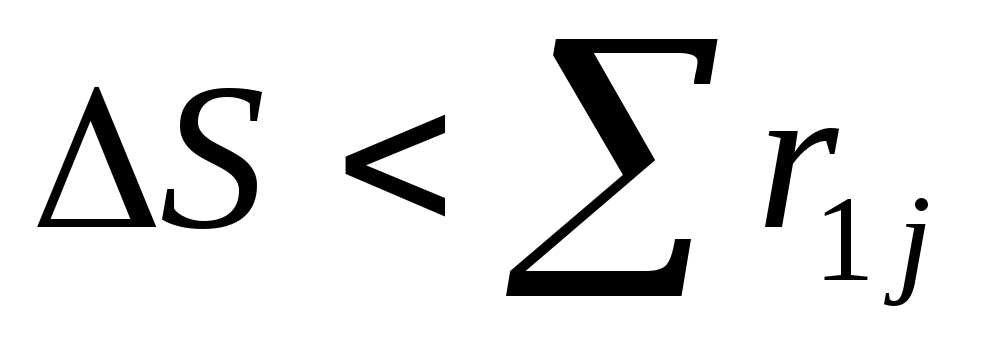, то вся недопоставка розподіляється довільним чином і процес розподілу завершений: 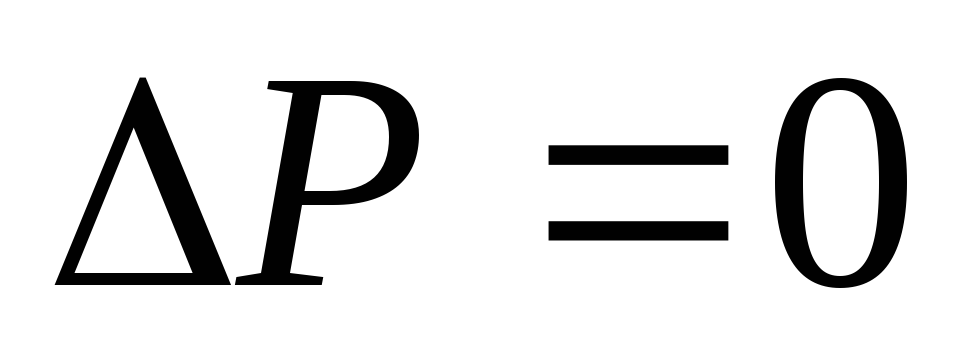. В протилежному випадку переходимо до наступного пункту.

3. Порівнюється сума повних резервів системи, рівна 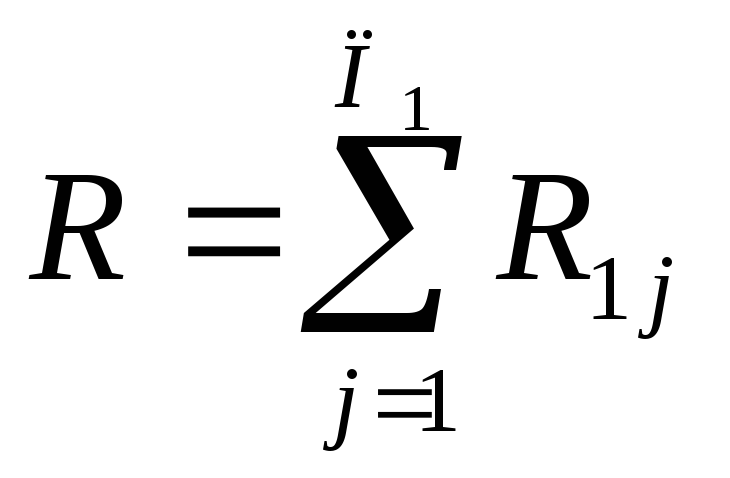, з величиною .

4. Якщо 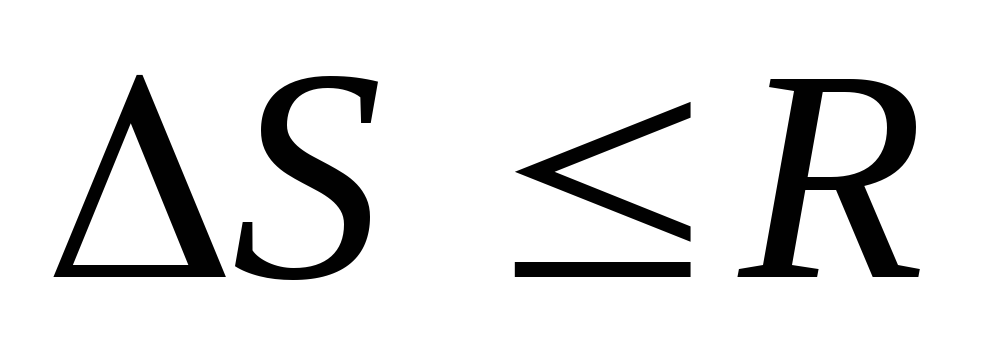, то переходимо до пункту 5, в іншому випадку – до пункту 7.

5. В кожну вершину першого етапу направляється недопоставка об’ємом 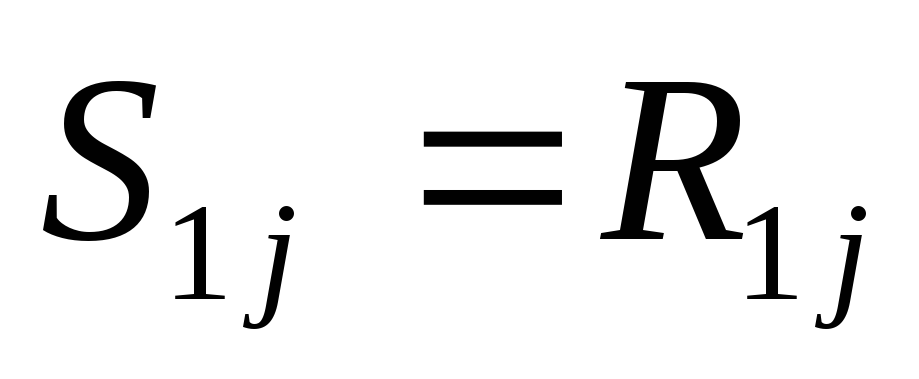, в результаті чого з j-вершини першого етапу вийде на другий етап недовипуск продукції, рівний 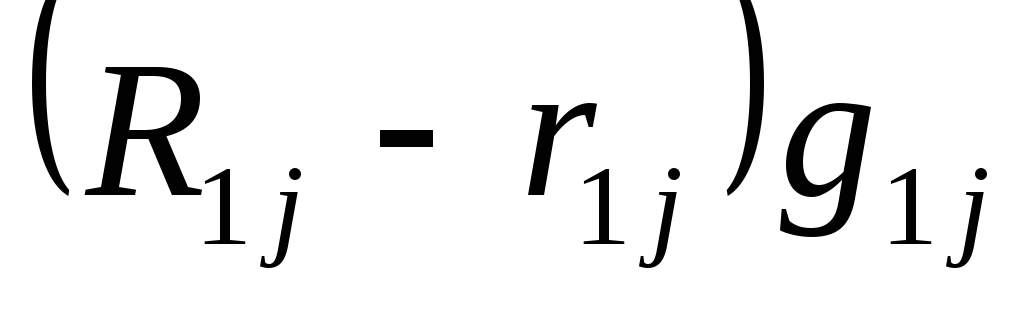. Цей недовипуск спричиняє недопоставку до всіх об’єктів другого етапу, пов’язаних з j-елементом першого етапу.

6. Недовипуск продукції першого етапу розподіляється в суміжні вершини другого етапу – так само, як і в п.5. Тоді – перехід до вершин третього етапу, де недовипуск розподіляється аналогічно. Цей процес продовжується до останнього етапу. Відповідно до співвідношень (8)-(10) недовипуск продукції в системі буде нульовим або на одному з проміжних етапів, або на останньому.

7. Якщо 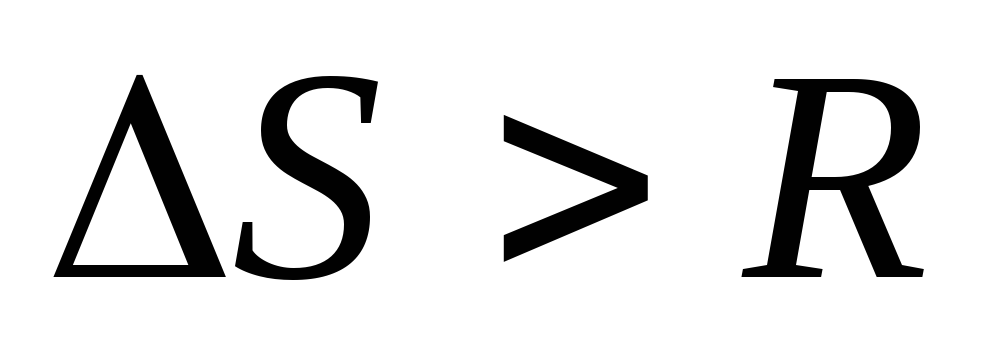, то розподіл здійснюється так само, як це описано в п.5 чи в п.6, але не всієї недопоставки , а тільки об’єм R.

8. Інша частина недопоставки 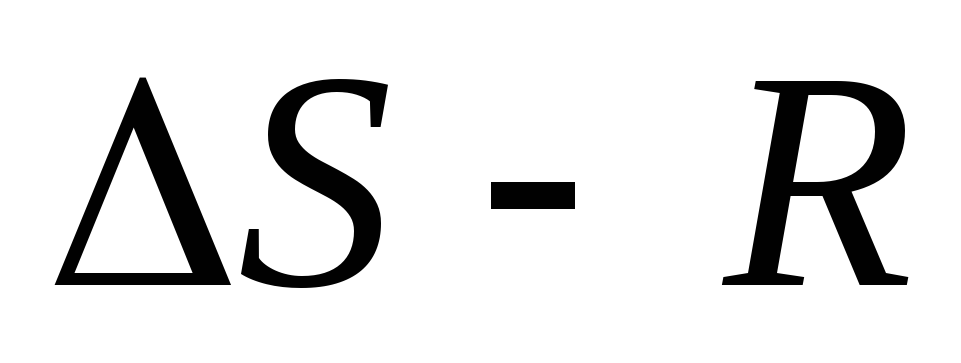розподіляється по еластичному шляху в припущенні, що в жодного елемента системи резервів немає.

Таким чином, функцію еластичності складної системи можна записати у вигляді:

(11)

де коефіцієнт жорсткості еластичного шляху в системі, а R – її повний резерв, розрахований на основі співвідношень (8)-(10) так, як було описано вище.

Формула (11) дозволяє визначити показник надійності системи:

Висновок

Надійність можна підвищити за рахунок зменшення коефіцієнтів жорсткості еластичного шляху та за рахунок повних резервів. Перший з цих принципів тісно пов'язаний з технологією виробництва продукції, другий – з формуванням резервів, але оскільки і вибір еластичного шляху, і формування повних резервів системи залежать від топології економічних зв’язків в ній, то управляти надійністю плану системи можна шляхом створення шляхів, які забезпечують підвищення надійності, наприклад, створенням паралельних ланцюжків виробництва і переходу між ними.

Ці принципи можуть бути прив’язані також до показників витрат на забезпечення надійності: при заданому рівні витрат можна говорити, наприклад, про максимальну надійність системи, а при заданому рівні її надійності – про оптимальні витрати на її забезпечення.

Список використаної літератури:

1. Биткова Т.В., Иванов С.Н. Экономическое моделирование. – в кн.: Прикладная экономика. Т.1. – ДонНУ, 2000,

стр. 22-16.

2. Моделювання системних характеристик в економіці: навч. посіб. / [Лавінський Г. В., Пшенишнюк О. С., Устенко С. В., Шарапов О. Д.]. – К.: ЕКМО, 2004. – 169 с.

14