Міністерство освіти і науки України

Львівський національний університет імені Івана Франка Економічний факультет

Кафедра

економічної кібернетики

Індивідуальне завдання №1

з курсу "Моделювання системних характеристик в економіці" на тему:

“Алгоритм розв’язання багатокритеріальної задачі розподілу збурень”

Виконали:

студенти групи

ЕккМ – 51с

Крамар Наталя

Берко Євген

Викладач :

Антонів В.Б.

Львів 2011

План:

Вступ

1. Залежність можливості погашення збурень (адаптації) від еластичності

2. Планова задача окремого елемента системи в умовах дисбалансу

3. Еластичний шлях

4. Розрахунок резервів для системи

5. Багатокритеріальна задача розподілу збурень та алгоритм її розв’язання Висновок

Список використаної літератури

Вступ

Будь-яка реальна економіка, незалежно від рівня ієрархії, будучи складною та багатоетапною, складається з елементів економічно пов’язаних локальних підсистем.

Адаптивні властивості плану такої системи відносно діючих на неї можливих збурень залежать не тільки від набору елементів системи, але і від топології їх технологічних, фінансових, транспортних, інформаційних зв’язків, тобто від структури системи.

Спектр можливих збурень складної системи доволі широкий: ймовірнісно-невизначені рівні поставок, коливання попиту на продукцію системи, можливі технологічні збої, які викликаються, наприклад, прийомом нових, іще не повністю освоєних, науково-технічних досягнень, недостатньо обґрунтовані норми ціни, ненадійний інформаційний обмін в системі, нераціональна або слаборозвинута інфраструктура, соціальні і демографічні фактори і т. д.

Разом з промисловими комплексами, де переважає технологічний тип зв’язків, взаємообумовлені, і, як правило, мають складну структуру виробничо-економічних зв’язків системи інвестицій. В таких системах в якості одного із специфічних видів ресурсів виступає час. Його розподіл зазвичай задається сітьовою моделлю реалізації інвестиційного проекту. Термін закінчення того чи іншого етапу виробництва можна розглядати так, як і один із видів продукції системи та її елементів.

Клас задач, який тут розглядається, стосується питань вивчення розподілу збурень, що виникають або ж в самій даній системі, або в системі, суміжній з нею. Кожне збурення, яке йде від яких-небудь підсистем, ініціює подальші збурення на інших елементах і зв’язках.

Аналіз збурень повинен разом з аналізом вхідних параметрів системи або її елементів включати і аналіз компенсуючих можливостей елементів системи, які в тій чи іншій мірі є в будь-якій системі.

Враховуючи складність економічних систем, моделлю такого аналізу може служити багатоцільова задача оптимізації.

1. Залежність можливості погашення збурень (адаптації) від еластичності

Теоретично будь-яке збурення потребує перегляду плану всієї системи. Застосувати до реальних систем багатократні перерахунки для аналізу якості плану практично неможливо, а багато раціональних зв’язків можуть бути установлені і без оптимізаційних розрахунків. Крім того, аналіз можна проводити по окремих, найбільш напружених зв’язках, вказувати напрямки їх розвантаження. Звідси виходить, що необхідно мати принципи управління рухом збурень, направляючи їх в ті елементи системи, які найкраще можуть їх погасити.

Представимо функцію еластичності у вигляді:

(1)

∆S/S - вектор, який характеризує якість входу системи;

∆P/P - вектор якості виходу системи;

α – вектор-параметр, який характеризує структуру системи.

Якщо припустити, що залежність має лінійний вид, отримаємо:

(2)

G(a) - матриця жорсткості, яка найкращим способом відображає зв'язок ∆P/P і ∆S/S.

Нехай, наприклад, S – вектор планових поставок ресурсів; ∆S – абсолютні значення їх недопоставки; P – вектор планового випуску продукції системи; ∆Р – вектор недовипуску продукції; α – вектор-парметр, який характеризує зваженість різних критеріїв, якщо оптимізація цільова; забезпеченість дефіцитними ресурсами; взаємозамінність продукції, технологічних способів і т. д.

Було відмічено, що план з більш пологою функцією еластичності є бажанішим. Тому можлива постановка таких задач, як сортування планів за їхніми функціями еластичності; побудова плану з більш пологою чи заданою функцією еластичності, постановка задач управління еластичністю, а відповідно прибутковістю планових показників.

Нормативний підхід в побудові надійних планів пропонує таке, що які б не були реальні умови розвитку системи, взаємозв’язок входу і виходу в ній повинні безпосередньо підпорядковуватись визначеним співвідношенням. Нормативи надійності, в залежності від стану економічної системи можуть задаватися або виходячи із рівня надійності метасистеми (тобто системи, яка включає дану в якості підсистеми), або на основі цілей самої системи.

Таким чином, можлива постановка задачі управління надійністю плану системи, зокрема побудова плану із заданою надійністю. Крім того, постає задача управління еластичністю складної системи через еластичності її елементів. Функція еластичності складної системи являється суперпозицією функцій еластичності її елементів і залежить від цілого комплексу їх зв’язків, зокрема, від топологічної структури системи.

Приклад. Розглянемо виробничу систему. Виробництво продукції можна розділити на 3 етапи ( і= 1, 2, 3). На першому етапі функціонують два об’єкти, на другому – три, на третьому – два. Структура виробничих зв’язків представлена на рис. 1.

Кожне збурення в подібній мережі виробничих зв’язків передається по ланцюгу з етапу на етап. Крім того, люба із вершин мережі сама може стати «генератором» збурень. Можна припускати відсутність горизонтальних (тобто всередині основного етапу) і зворотних зв’язків і вважати, що збурення йдуть з першого етапу до всіх наступних. Якщо це не так – то можна ввести фіктивні вершини і зв’язки в мережі і розгорнути мережу в динаміці, коли один і той самий об’єкт системи в різні моменти часу задається різними вершинами мережі.

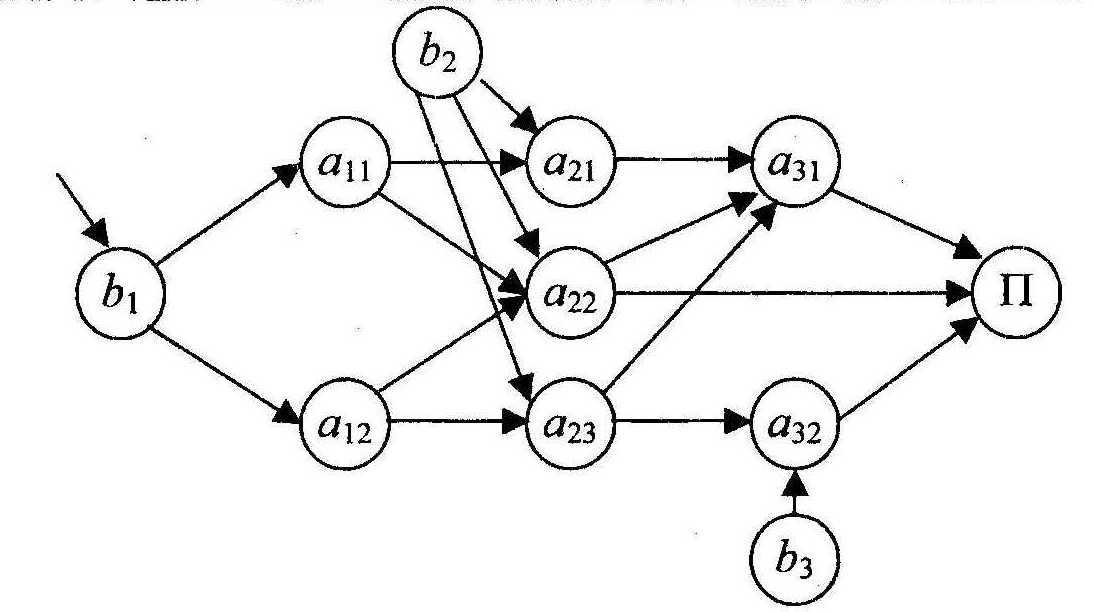
Рис. 1. Структура виробничої системи

- j-ий об’єкт на і-му етапі виробництва;

- генератор збурень на і-му етапі;

П – кінцевий продукт системи.

На рис.2 вершини з верхніми індексами – фіктивні, наприклад, вершина означає, що продукція вершини абсолютно без всяких втрат передається транзитом через вершину у вершину П. Те саме можна сказати і про збурення , і

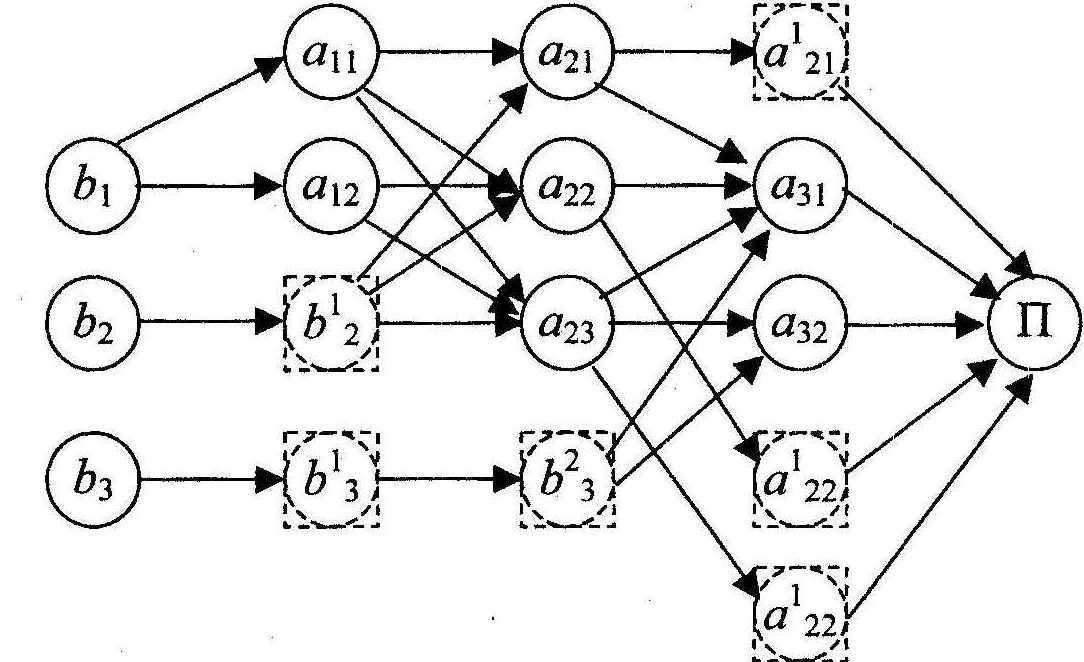
Рис.2. Структура виробничої системи з розподілом впливу в часі.

Система, яка розвивається із зворотнім зв’язком, може бути представлена з розподілом моментів мережею з двома входами збурень і двома виходами. Якщо всі можливі (як по типу, так і по часу) збурення і випуски кінцевого продукту системи задавати у вигляді векторів, то мережа може бути представлена з одним входом і одним виходом.