
§ 5. Векторные пространства.
Пример 1. Доказать, что следующее
множество образует векторное пространство
над полем
![]() относительно операций сложения матриц
и умножения матриц на число.
относительно операций сложения матриц
и умножения матриц на число.
Найти его базис и размерность.
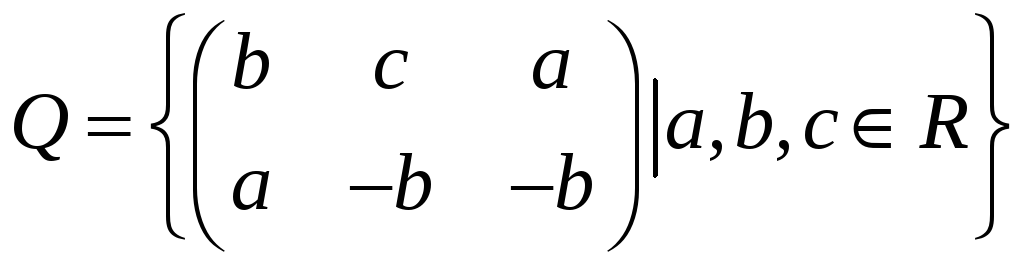 .
.
Решение.
![]() является непустым подмножеством
пространства матриц размерности
является непустым подмножеством
пространства матриц размерности
![]() .
Докажем, что
.
Докажем, что
![]() является подпространством в
является подпространством в
![]() ,
пользуясь критерием подпространства.
Пусть
,
пользуясь критерием подпространства.
Пусть
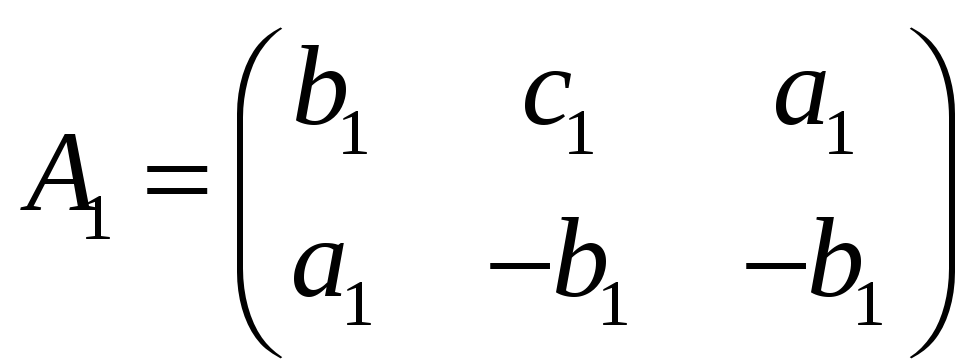 и
и
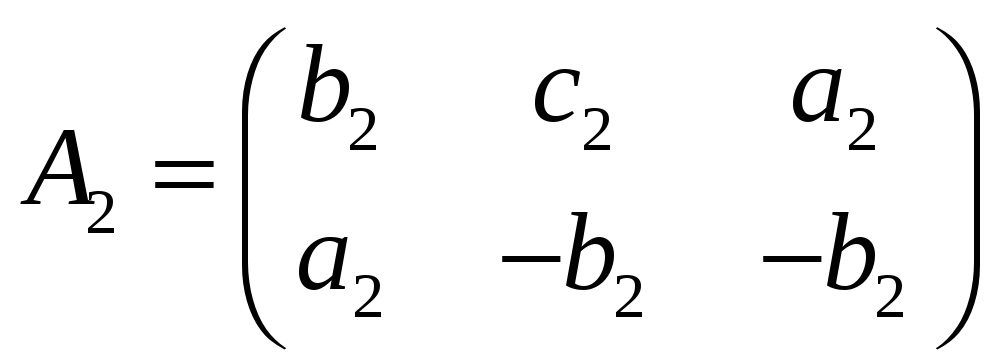
произвольные матрицы из
![]() .
Рассмотрим их сумму
.
Рассмотрим их сумму
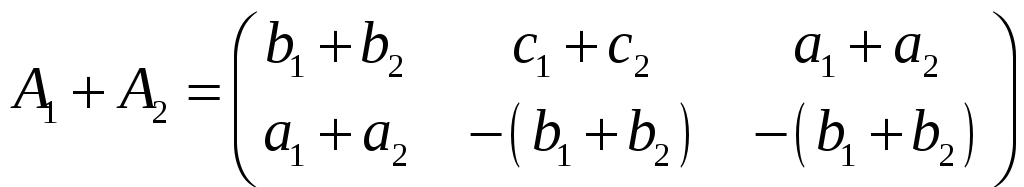 .
.
Очевидно
![]() .
Произведение
.
Произведение
![]() на любое число
на любое число
![]()
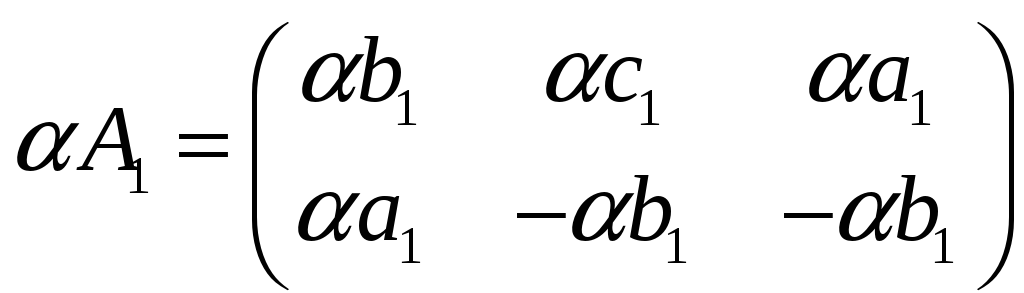
также принадлежит
![]() .
Итак,
.
Итак,
![]() является подпространством пространства
является подпространством пространства
![]() ,
а значит, само является пространством.
,
а значит, само является пространством.
Найдем базис этого пространства.
Ясно, что в базис можно включить, например,
![]() , так как
, так как
![]() .
.
Так как ![]() , то
, то
![]() нельзя получить в виде
нельзя получить в виде
![]() .
Поэтому в качестве второго базисного
вектора можно взять
.
Поэтому в качестве второго базисного
вектора можно взять
![]() .
Рассмотрим вектор
.
Рассмотрим вектор
![]() .
Его нельзя представить в виде линейной
комбинации
.
Его нельзя представить в виде линейной
комбинации
![]() и
и
![]() ,
так как
,
так как
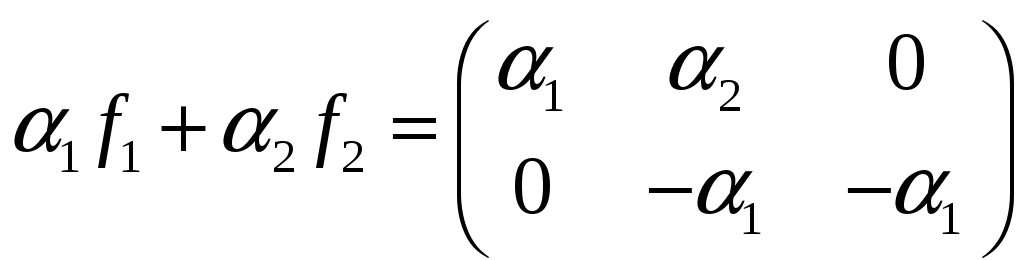 .
Поэтому в качестве третьего базисного
вектора возьмем
.
Поэтому в качестве третьего базисного
вектора возьмем
![]() .
Всякий другой вектор
.
Всякий другой вектор
![]() можно представить в виде линейной
комбинации
можно представить в виде линейной
комбинации
![]() .
.
![]() .
.
Следовательно, система векторов
![]() является системой образующих пространства
является системой образующих пространства
![]() .
По построению, эта система линейно
независима. Значит, она является базисом.
.
По построению, эта система линейно
независима. Значит, она является базисом.
Пример2. Выяснить, является ли
система векторов
![]() линейно зависимой. Найти коэффициенты
линейной зависимости.
линейно зависимой. Найти коэффициенты
линейной зависимости.
Решение. Пусть
![]() ,
где
,
где
![]() — некоторые числа. Подставляем в это
равенство векторы
— некоторые числа. Подставляем в это
равенство векторы
![]() .
.
![]() .
.
После выполнения операции над векторами получаем
![]() ,
откуда
,
откуда
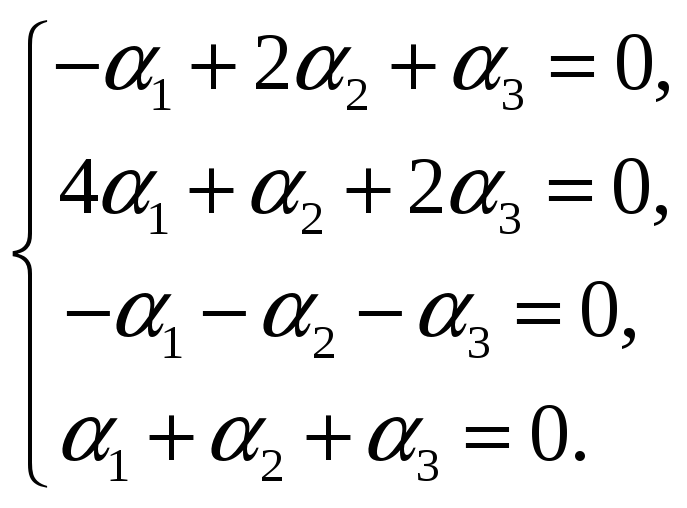
Эту систему линейных уравнений решаем методом Гаусса:
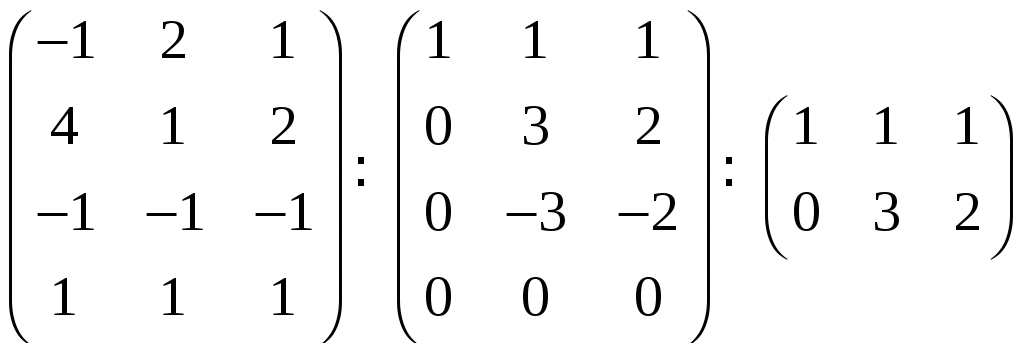 .
.
Получилась трапецеидальная система
уравнений. Она является неопределенной
и потому имеет ненулевые решения (кроме
нулевого). Таким образом, система
![]() линейно зависима. Найдем коэффициенты
линейной зависимости. Для этого решаем
однородную систему линейных уравнений,
приведенную к трапецеидальному виду
линейно зависима. Найдем коэффициенты
линейной зависимости. Для этого решаем
однородную систему линейных уравнений,
приведенную к трапецеидальному виду
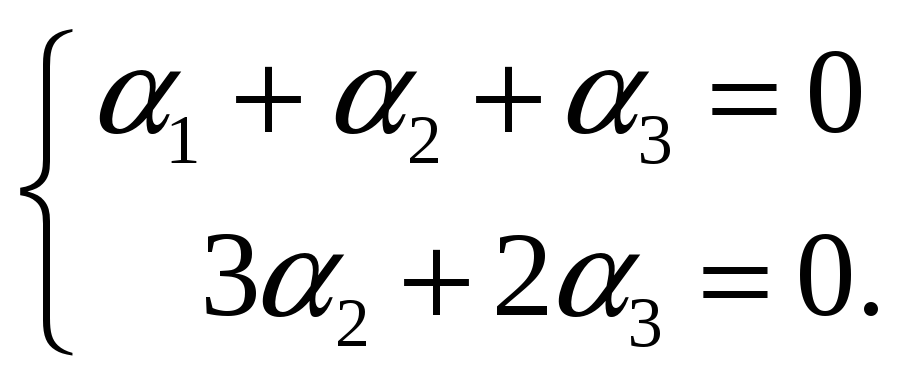
Общее решение этой системы имеет вид
![]() .
.
Найдем частное решение, придавая
![]() произвольное значение, отличное от
нуля, например, -3. Получим
произвольное значение, отличное от
нуля, например, -3. Получим
![]() .
Таким образом,
.
Таким образом,
![]() .
Очевидно, коэффициенты линейной
зависимости определяются неоднозначно.
.
Очевидно, коэффициенты линейной
зависимости определяются неоднозначно.
Пример 3. Найти какую-нибудь максимальную линейно независимую подсистему данной системы векторов, а остальные векторы выразить через нее.
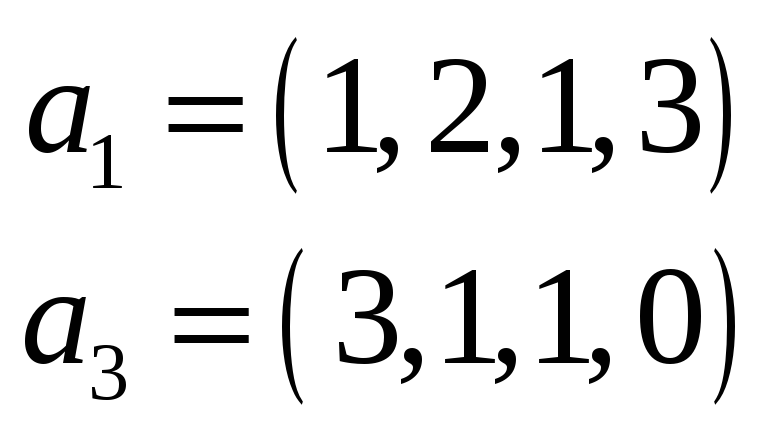
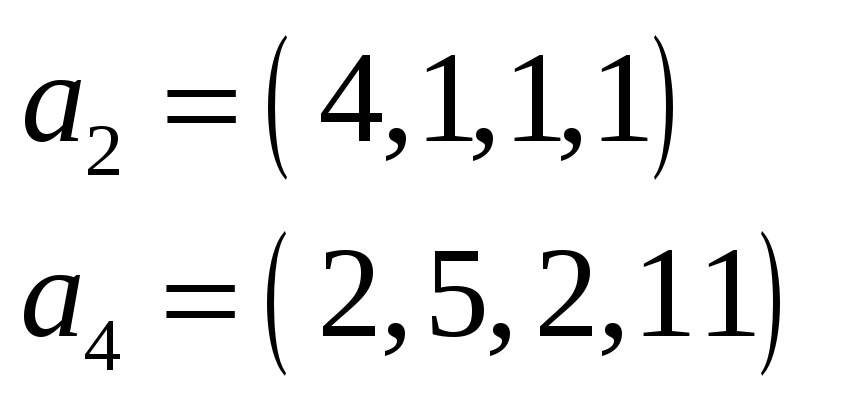
Решение. Составим матрицу
![]() ,
столбцами которой являются данные
векторы, и найдем ее ранг. Будем делать
элементарные преобразования только
над строками.
,
столбцами которой являются данные
векторы, и найдем ее ранг. Будем делать
элементарные преобразования только
над строками.

Первую строку, умноженную на соответствующие числа -2, -1, -3, прибавили ко второй, третьей, четвертой. Третью строку, умноженную на соответствующие числа -2, -4, прибавили ко второй и четвертой. И наконец, третью, умноженную на 2, прибавили к четвертой. Так как минор третьего порядка
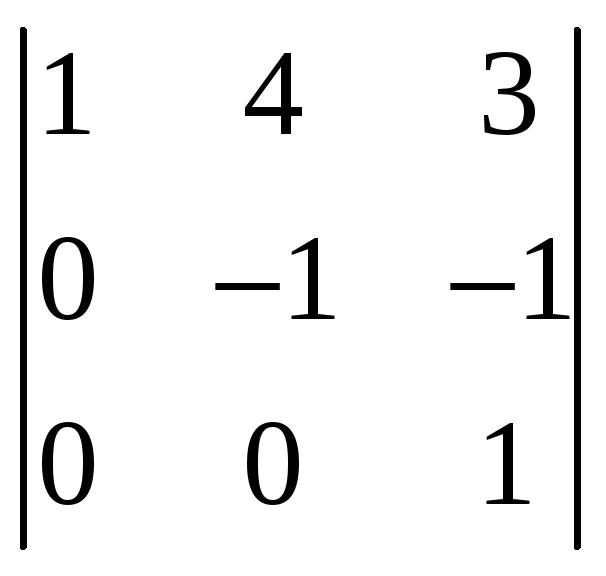
Отличен от нуля, а определитель четвертого
порядка равен нулю, то ранг последней
матрицы, а значит, ранг матрицы
![]() равен 3. Отсюда следует, что ранг данной
системы равен 3.
равен 3. Отсюда следует, что ранг данной
системы равен 3.
Три вектора входят в максимальную
линейно независимую подсистему данной
системы. Очевидно, что это векторы
![]() .Действительно,
выразим вектор
.Действительно,
выразим вектор
![]() через
через
![]() :
:
![]() .
Подставим в это уравнение выражения
векторов
.
Подставим в это уравнение выражения
векторов
![]() .
После выполнения операций над векторами
получим:
.
После выполнения операций над векторами
получим:
![]() .
Приравнивая соответствующие координаты,
получим систему линейных уравнений:
.
Приравнивая соответствующие координаты,
получим систему линейных уравнений:
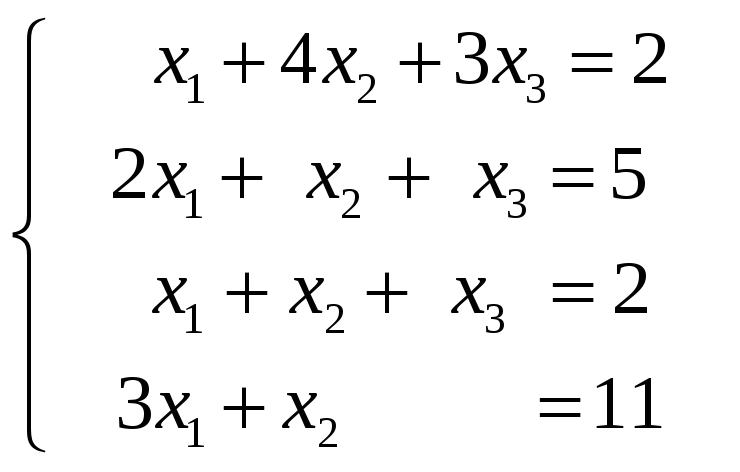 .
.
Решаем эту систему методом Гаусса. Составим расширенную матрицу
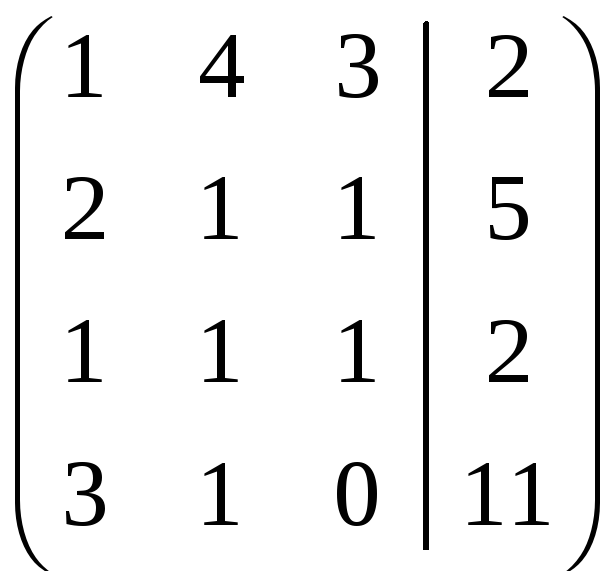 .
.
Эта матрица совпадает с матрицей
![]() .
Так как мы проделываем элементарные
преобразования над строками матрицы
.
Так как мы проделываем элементарные
преобразования над строками матрицы
![]() ,
то эта система эквивалентна системе
линейных уравнений, соответствующей
последней матрице:
,
то эта система эквивалентна системе
линейных уравнений, соответствующей
последней матрице:
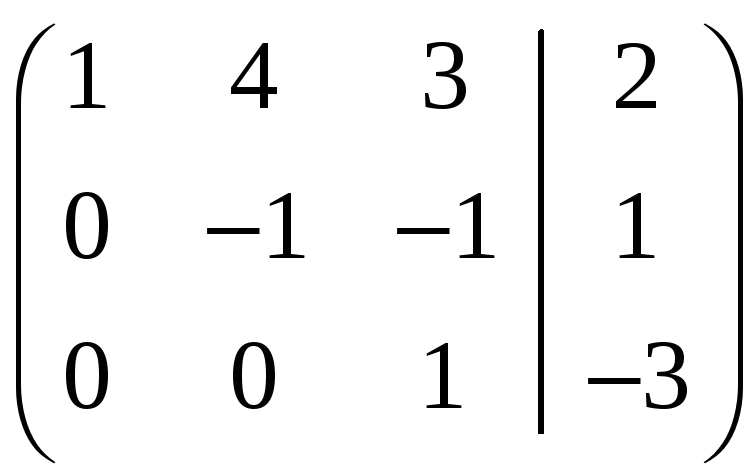 , то есть системе
, то есть системе
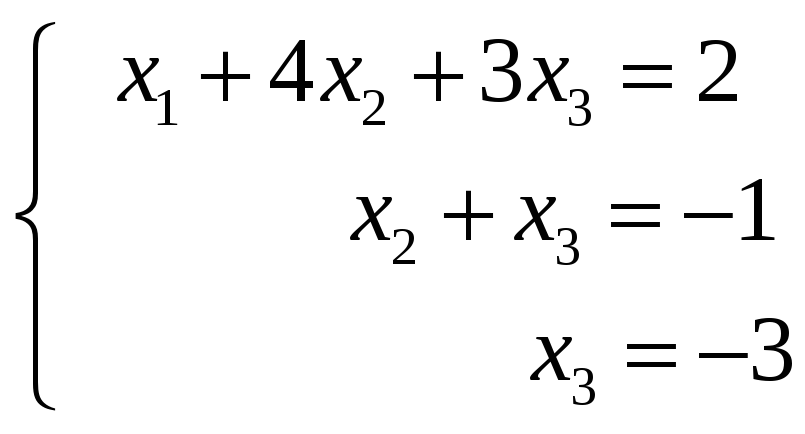 , откуда
, откуда
![]() ,
а следовательно,
,
а следовательно,
![]() .
.
Пример 4. Векторы
![]() заданы своими координатами в некотором
базисе
заданы своими координатами в некотором
базисе
![]() .
Показать, что векторы
.
Показать, что векторы
![]() сами образуют базис, и найти координаты
вектора
сами образуют базис, и найти координаты
вектора
![]() в этом базисе.
в этом базисе.
Решение. Так как система любых трех
линейно независимых векторов является
базисом 3-мерного пространства, то
достаточно доказать, что система
![]() линейно независима. Для этого составим
матрицу
линейно независима. Для этого составим
матрицу
![]() ,
столбцами которой являются координаты
векторов
,
столбцами которой являются координаты
векторов
![]() ,
и найдем ее ранг.
,
и найдем ее ранг.
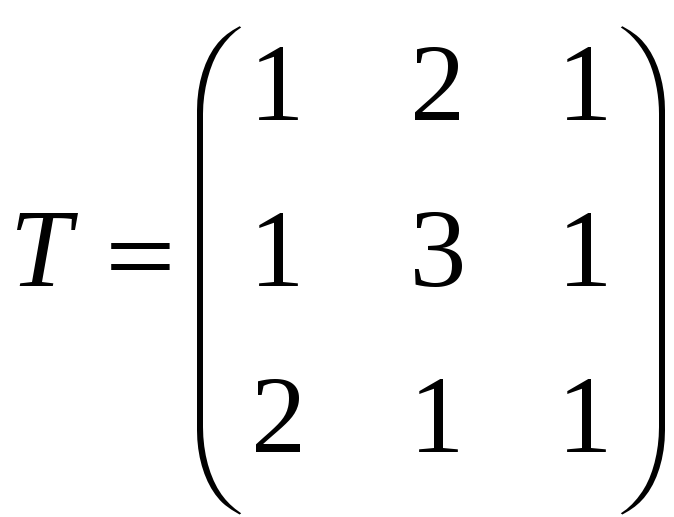 .
.
Определитель этой матрицы
![]() ,
а значит, по теореме о ранге, ранг матрицы
равен 3, что доказывает линейную
независимость системы
,
а значит, по теореме о ранге, ранг матрицы
равен 3, что доказывает линейную
независимость системы
![]() .
Таким образом,
.
Таким образом,
![]() образуют базис и
образуют базис и
![]() -матрица
перехода от базиса
-матрица
перехода от базиса
![]() к базису
к базису
![]() .
Для нахождения координат вектора в
базисе
.
Для нахождения координат вектора в
базисе
![]() воспользуемся формулой преобразования
координат, приведенной в
воспользуемся формулой преобразования
координат, приведенной в
![]() :
:
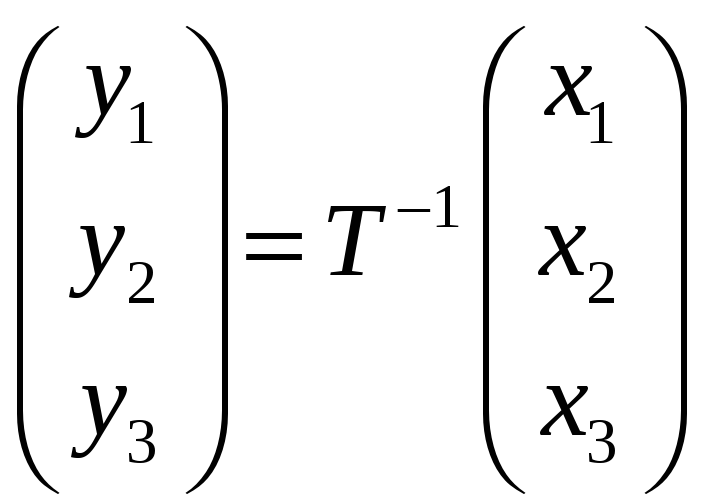 , где
, где
![]() — матрица перехода от базиса
— матрица перехода от базиса
![]() к базису
к базису
![]() ;
;
![]() — координаты вектора в базисе
— координаты вектора в базисе
![]() ;
;
![]() — координаты вектора
— координаты вектора
![]() в базисе
в базисе
![]() .
Так как здесь
.
Так как здесь
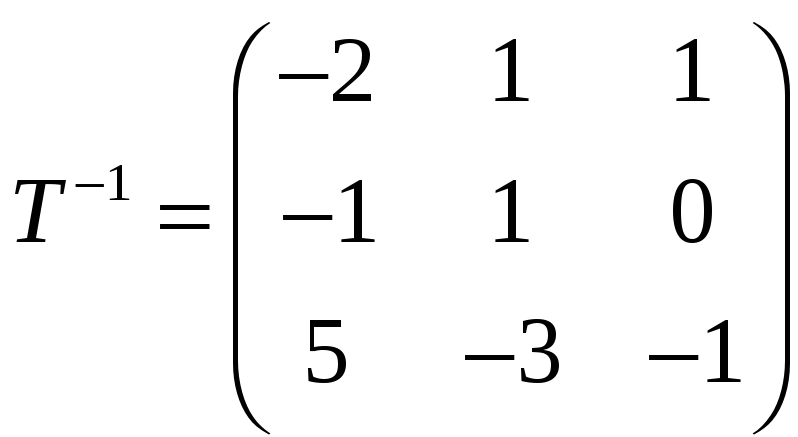 ,
то
,
то
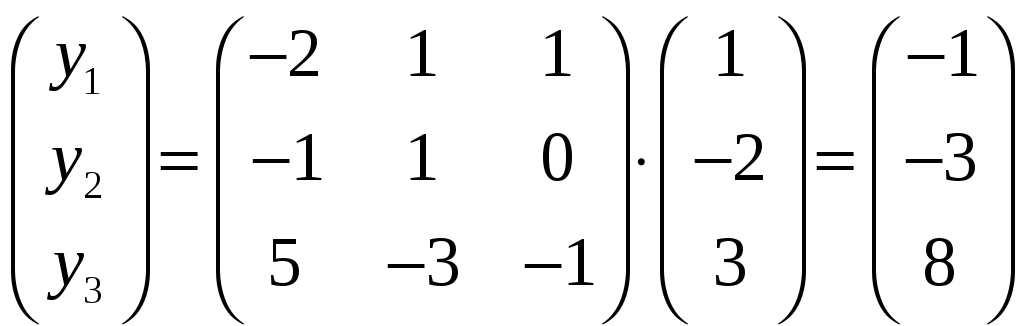 ,
,
Откуда
![]() ,
то есть
,
то есть
![]() .
.
Пример 5. Найти размерность и базис линейного подпространства, натянутого на векторы
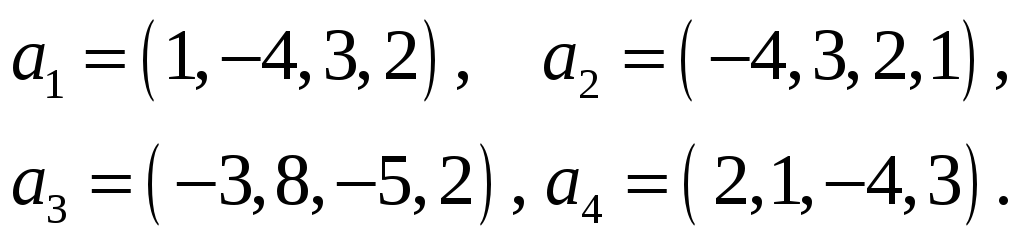
Решение. Базис линейного подпространства
![]() совпадает с максимальной линейно
независимой подсистемой системы векторов
совпадает с максимальной линейно
независимой подсистемой системы векторов
![]() (доказать!). Найдем эту подсистему, для
чего составим матрицу, столбцами которой
являются векторы
(доказать!). Найдем эту подсистему, для
чего составим матрицу, столбцами которой
являются векторы
![]() .
.
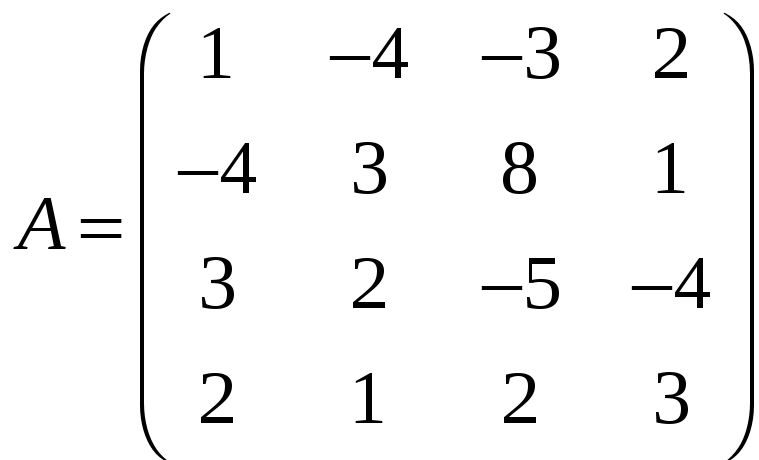 .
.
Найдем базисный минор этой матрицы. Так
как минор второго порядка
![]() ,
то рассмотрим минор 3-го порядка, его
окаймляющий
,
то рассмотрим минор 3-го порядка, его
окаймляющий
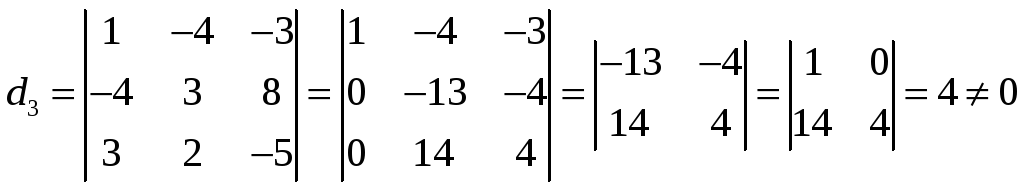 .
.
Теперь рассмотрим минор 4-го порядка,
окаймляющий минор 3-го порядка, отличный
от нуля. Это определитель матрицы
![]() .
.
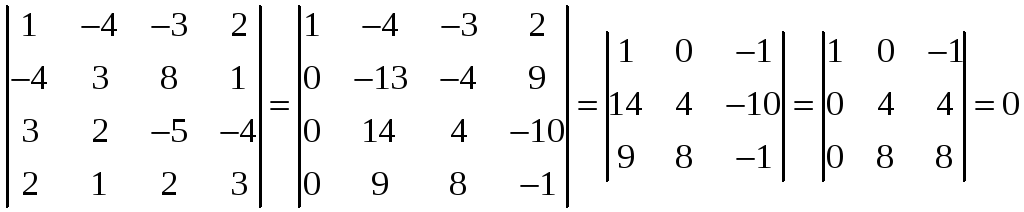 .
.
Он равен нулю. Значит,
![]() является базисным минором, то есть
минором наибольшего порядка, отличным
от нуля. А тогда
является базисным минором, то есть
минором наибольшего порядка, отличным
от нуля. А тогда
![]() образуют максимальную линейно-независимую
подсистему системы
образуют максимальную линейно-независимую
подсистему системы
![]() и тем самым
и тем самым
![]() образуют базис рассматриваемого
подпространства, причем размерность
подпространства равна 3.
образуют базис рассматриваемого
подпространства, причем размерность
подпространства равна 3.
Пример 6. Определить размерность и базис пространства решений однородной системы линейных уравнений.
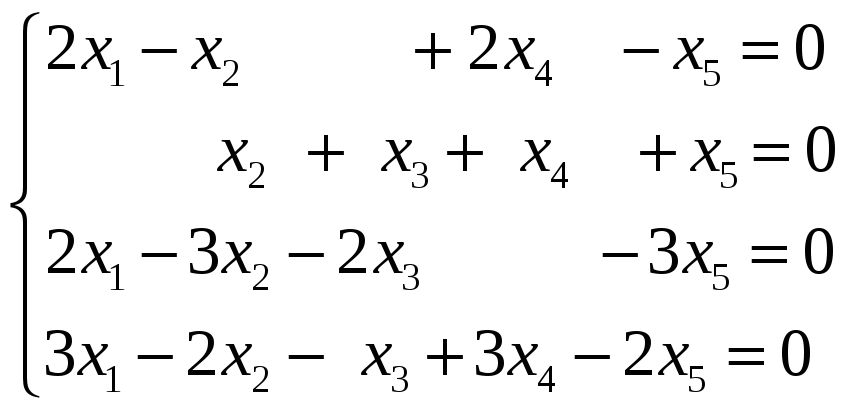
Решение. Множество всех решений
однородной системы линейных уравнений
образует векторное пространство
размерности
![]() ,
где
,
где
![]() — число неизвестных системы, а
— число неизвестных системы, а
![]() — ранг матрицы этой системы. Базис
образует система из любых
— ранг матрицы этой системы. Базис
образует система из любых
![]() линейно независимых частных решений.
Такая система решений называется
фундаментальной. Находим общее решение
системы методом Гаусса, для чего
составляем матрицу системы:
линейно независимых частных решений.
Такая система решений называется
фундаментальной. Находим общее решение
системы методом Гаусса, для чего
составляем матрицу системы:
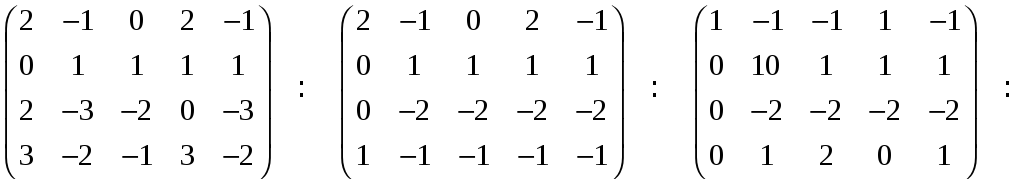
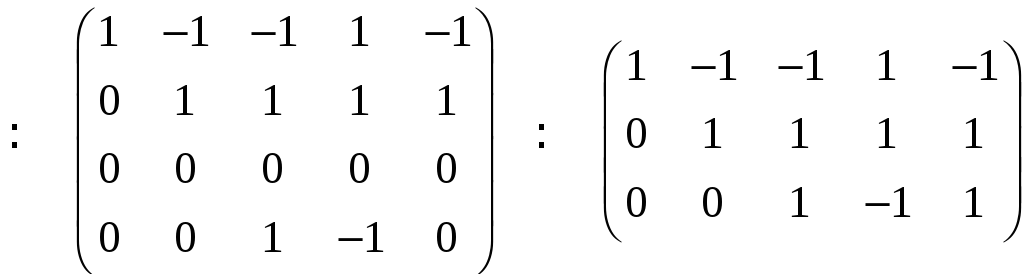 .
.
Ранг матрицы равен трем. Следовательно,
размерность пространства решений равна
2
![]() .
Данную систему уравнений заменим
эквивалентной системой:
.
Данную систему уравнений заменим
эквивалентной системой:
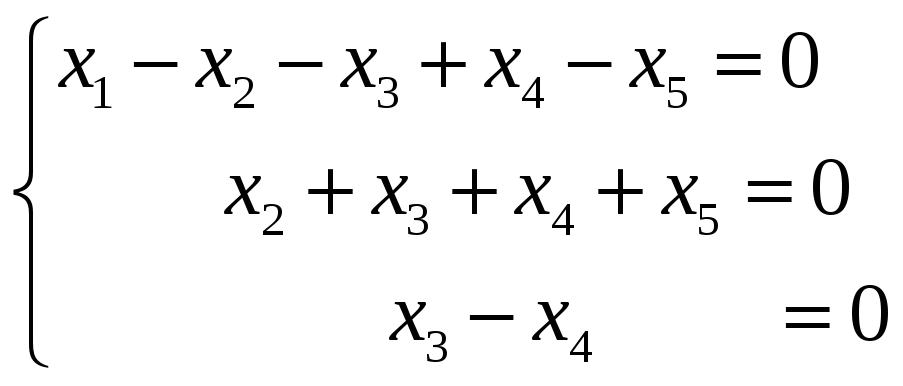
В качестве свободных неизвестных можно
взять
![]() .
Тогда
.
Тогда
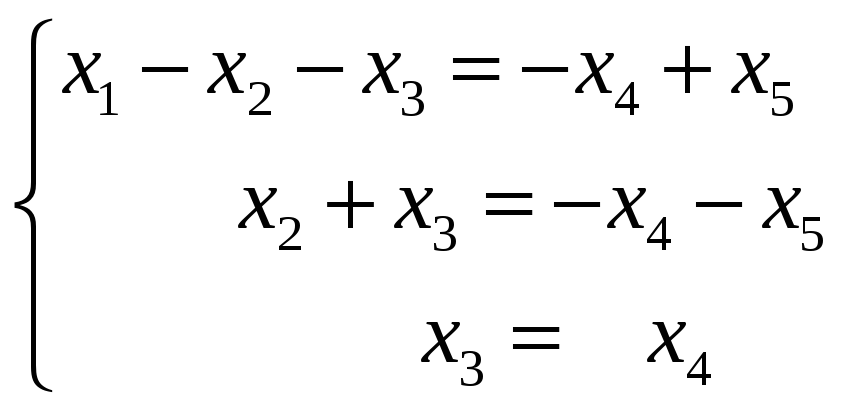
Общее решение системы имеет вид
![]() .
Находим два линейно независимых частных
решения. Для их нахождения мы два раза
придаем
.
Находим два линейно независимых частных
решения. Для их нахождения мы два раза
придаем
![]() и
и
![]() произвольные значения, но так, чтобы
определитель второго порядка, составленный
из этих значений, был отличен от нуля.
Положим
произвольные значения, но так, чтобы
определитель второго порядка, составленный
из этих значений, был отличен от нуля.
Положим
![]() ,
а затем
,
а затем
![]() и найдем
и найдем
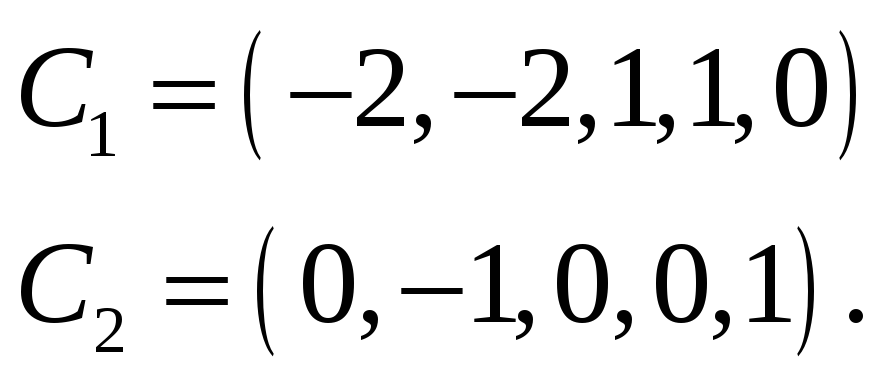
Мы получим один из базисов пространства решений данной однородной системы уравнений.
Пример 7. Найти базис и размерность
пересечения подпространств
![]() и
и
![]() ,
натянутых на системы векторов
,
натянутых на системы векторов
![]() и
и
![]() соответственно, если векторы заданы
координатами в некотором базисе
пространства.
соответственно, если векторы заданы
координатами в некотором базисе
пространства.
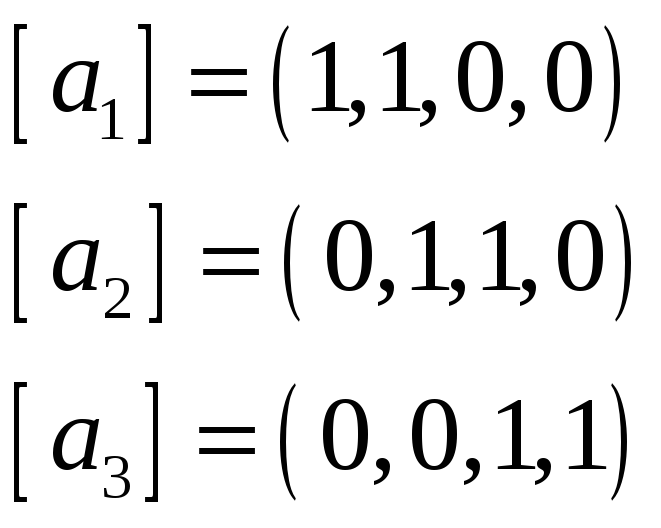
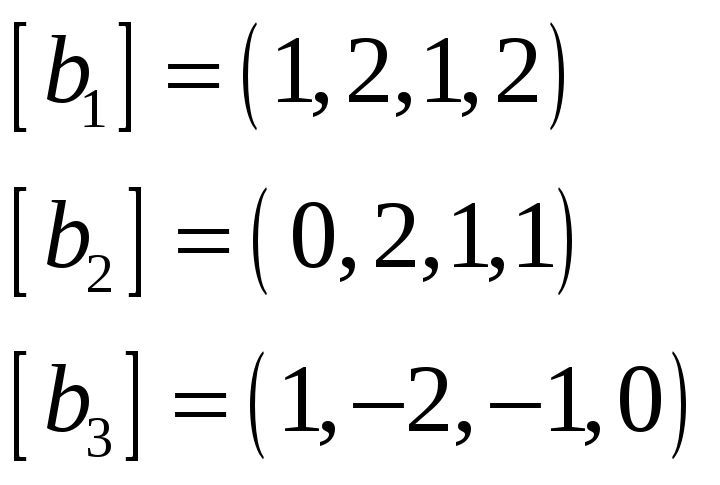
Решение. Вектор
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() линейно выражается через
линейно выражается через
![]() и через
и через
![]() .
А для этого необходимо и достаточно,
чтобы ранг матрицы
.
А для этого необходимо и достаточно,
чтобы ранг матрицы
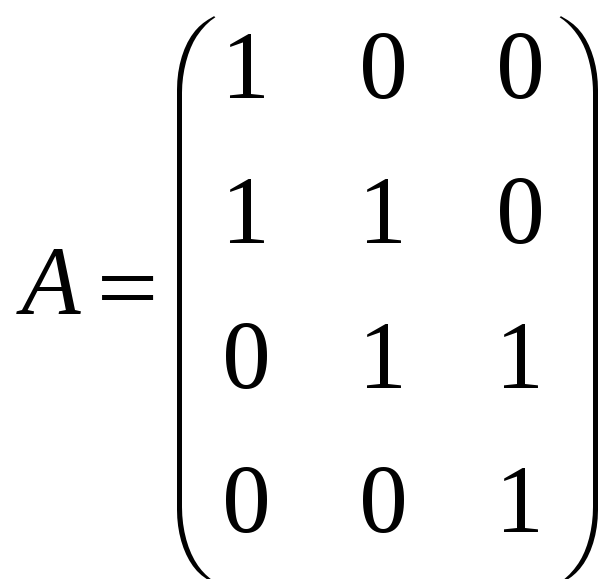
был равен рангу матрицы
![]()
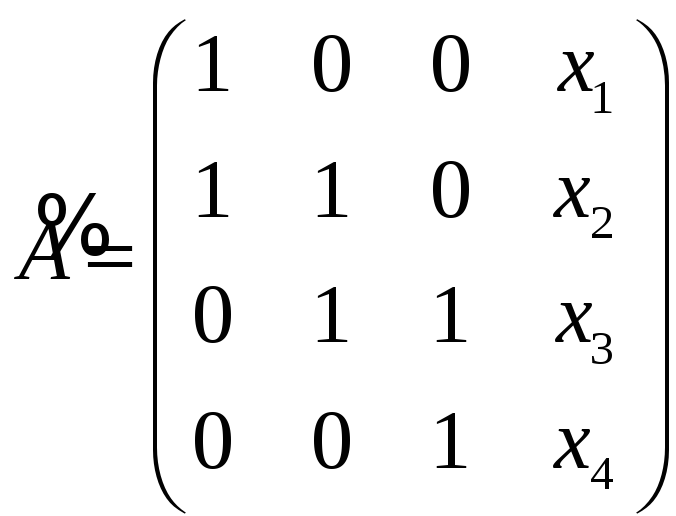
и ранг матрицы
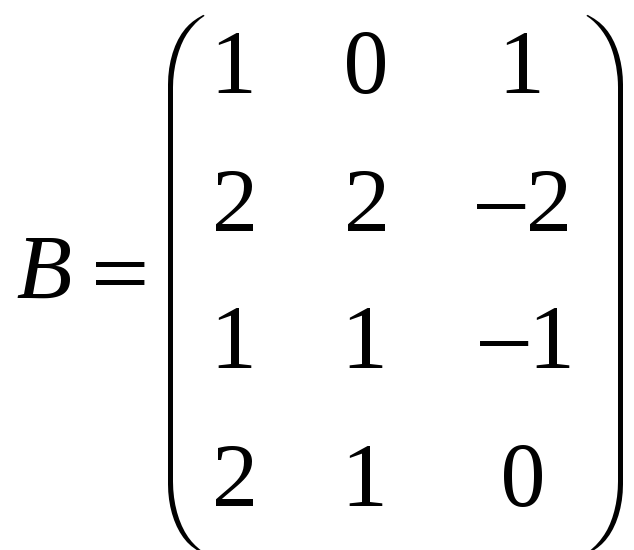
был равен рангу матрицы
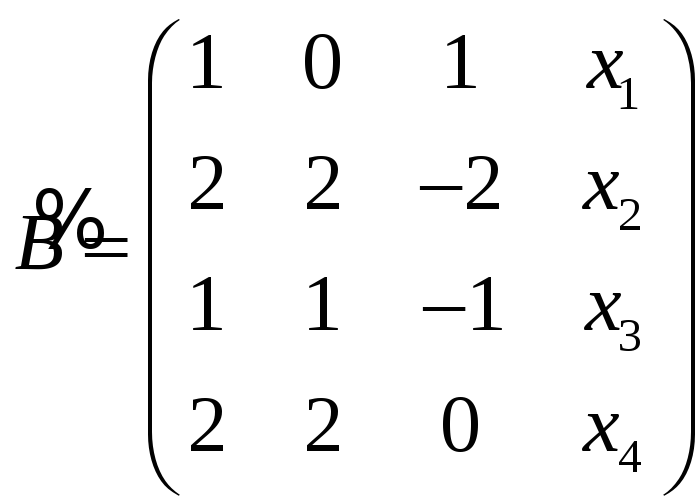 .
.
Выберем базисные миноры
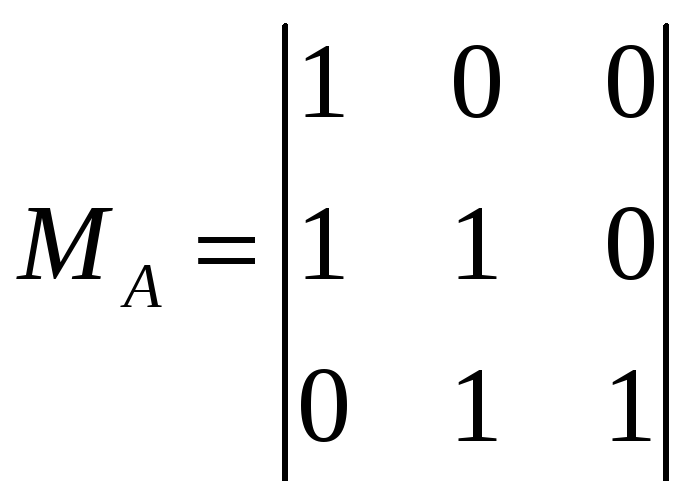 и
и ![]()
матриц
![]() и
и
![]() соответственно. Для того, чтобы
соответственно. Для того, чтобы
![]() и
и
![]() ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы
![]() был базисным минором в
был базисным минором в
![]() ,
а
,
а
![]() — в
— в
![]() .
Приравнивая нулю все миноры
.
Приравнивая нулю все миноры
![]() и
и
![]() ,
окаймляющие соответственно
,
окаймляющие соответственно
![]() и
и
![]() ,
содержащие столбец
,
содержащие столбец
![]() и имеющие порядок на единицу выше, чем
и имеющие порядок на единицу выше, чем
![]() и
и
![]() ,
получим систему линейных уравнений.
,
получим систему линейных уравнений.
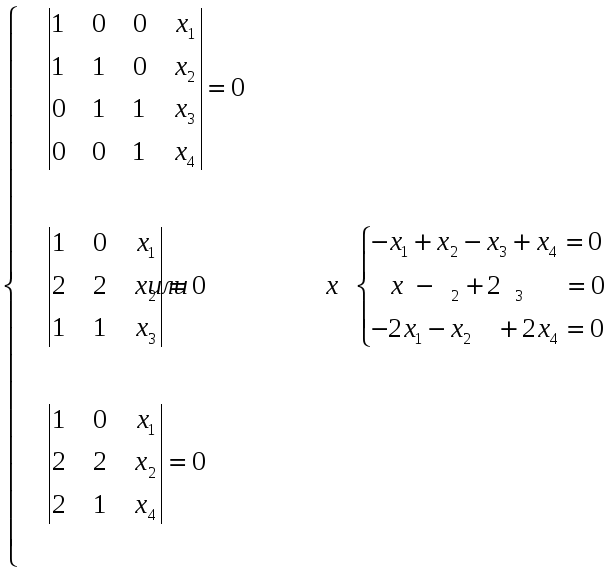
Решаем эту систему методом Гаусса.

![]() .
Общее решение имеет вид
.
Общее решение имеет вид
![]() .
Фундаментальная система состоит из
одного вектора
.
Фундаментальная система состоит из
одного вектора
![]() .
Следовательно, вектор
.
Следовательно, вектор
![]() образует базис подпространства
образует базис подпространства
![]() .
.
Литература: 3 — §17, 18
5 — №№ 608-613, 624-626, 636-650, 652-655, 661-669, 672, 674, 681, 689-695, 702-704, 712-714, 724-727, 1277-1293, 1296-1305, 1309-1311, 1317, 1318, 1320, 1321.
Контрольная работа 2
Найти значение многочлена
![]() и всех его производных в точке
и всех его производных в точке
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
Найти рациональные корни и определить их кратность.
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]() .
.
12.
![]() .
.
Разложить на неприводимые множители
над полем
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
Найти каноническое разложение многочлена над полем путем отделения кратных корней.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
Найти значение симметрического
многочлена
![]() на корнях многочлена
на корнях многочлена
![]() .
.
25.
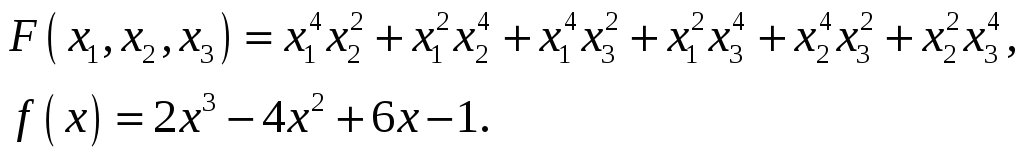
26.
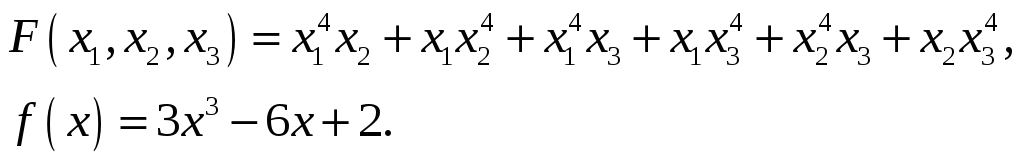
27.
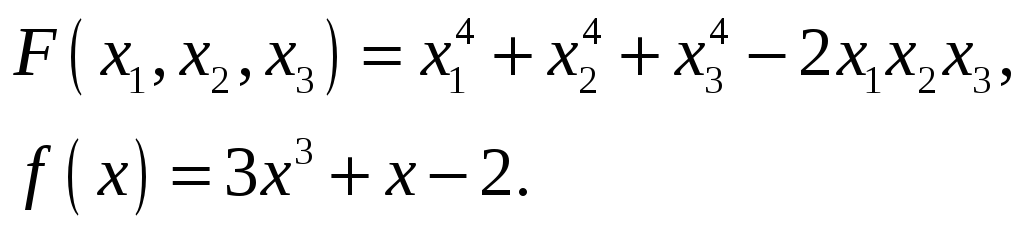
28.
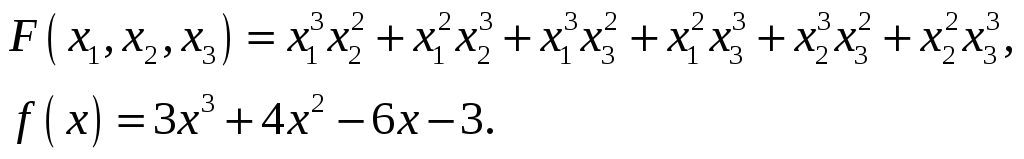
29.
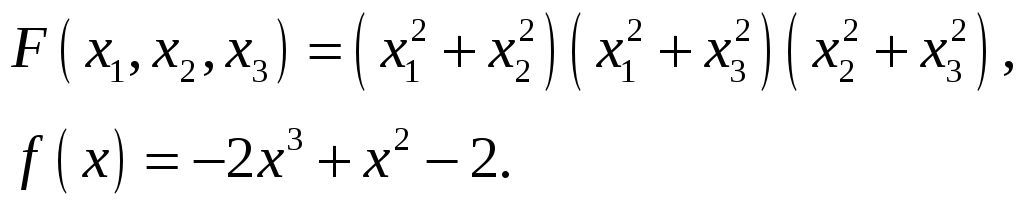
30.
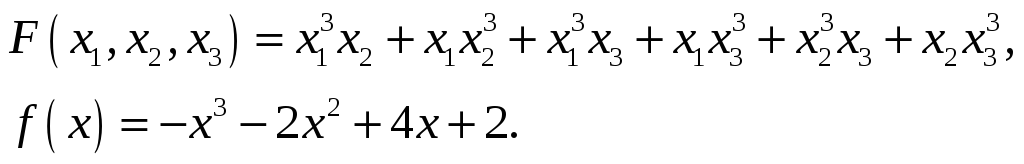
Доказать, что следующее множество
образует векторное пространство над
полем
![]() .
Найти его базис и размерность.
.
Найти его базис и размерность.
31.
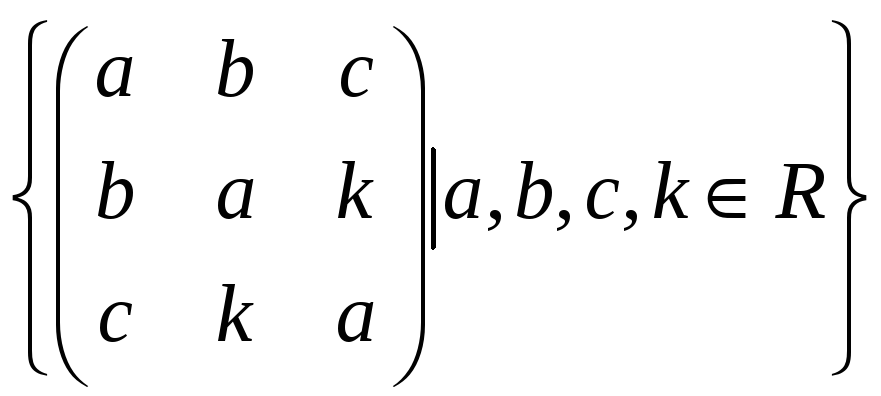 .
.
32.
![]() .
.
33.
![]() .
.
34.
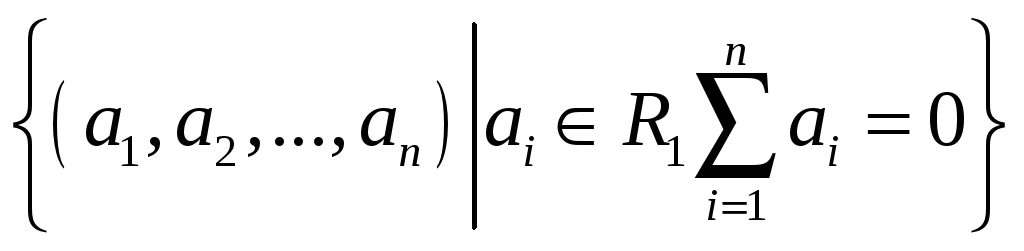 .
.
35.
![]() .
.
36.
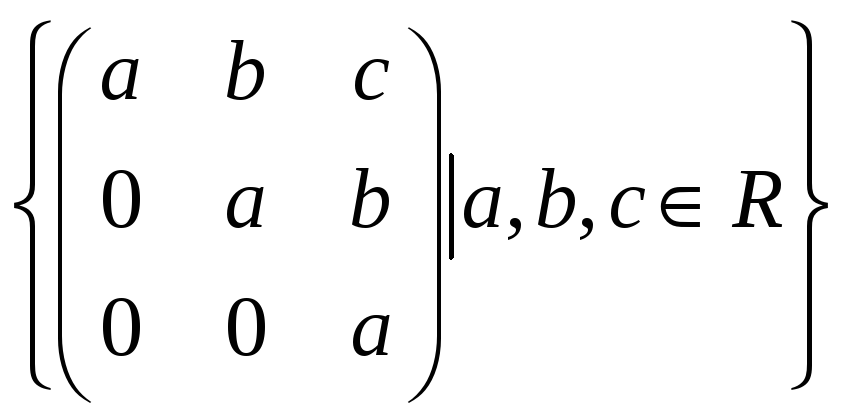 .
.
Выяснить, является ли система векторов линейно зависимой. Найти коэффициенты линейной зависимости.
37.
![]()
38.
![]()
39.
![]()
40.
![]()
41.
![]()
42.
![]()
Найти какую-нибудь максимальную независимую подсистему данной системы векторов, а остальные векторы выразить через нее.
43.
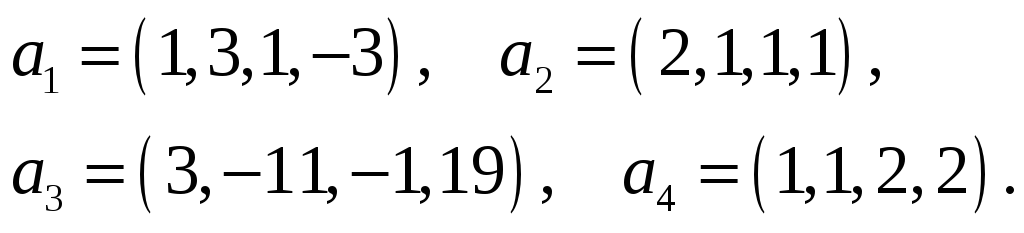
44.
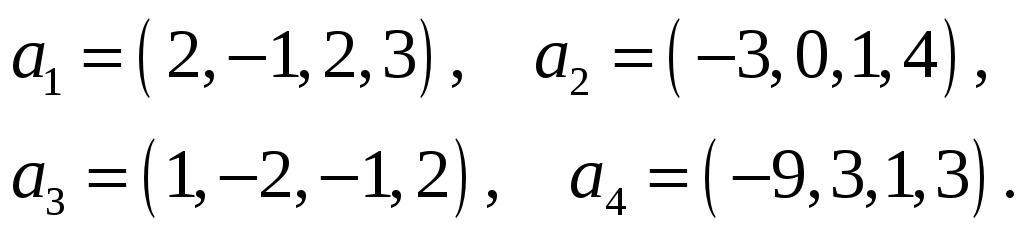
45.
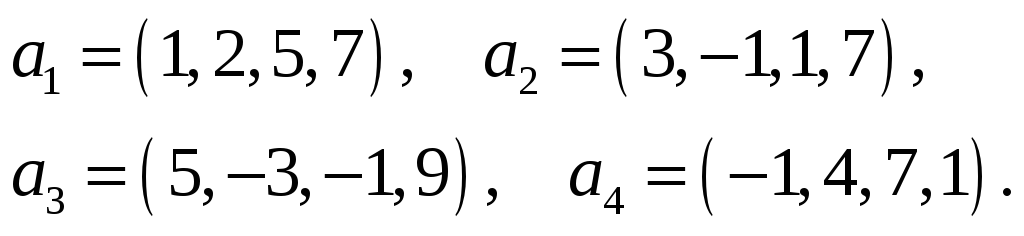
46.
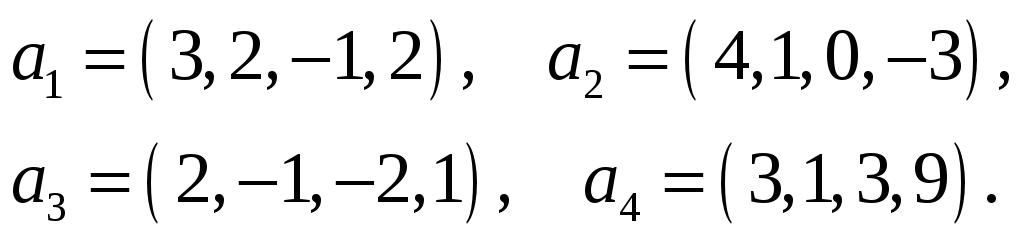
47.
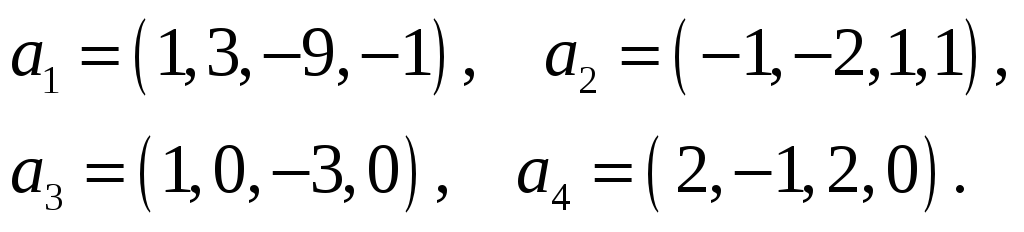
48.
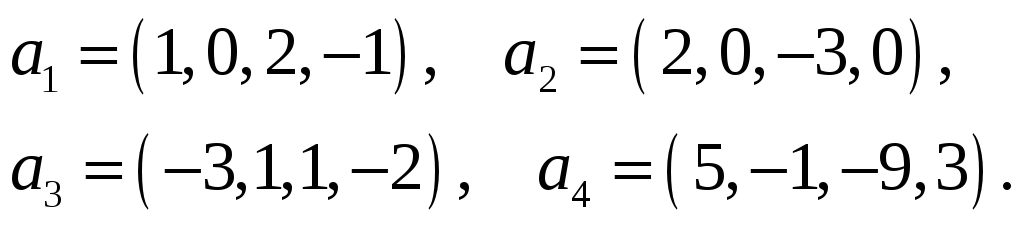
Векторы
![]() и
и
![]() заданы своими координатами в некотором
базисе
заданы своими координатами в некотором
базисе
![]() .
Показать, что векторы
.
Показать, что векторы
![]() сами образуют базис, и найти координаты
вектора
сами образуют базис, и найти координаты
вектора
![]() в этом базисе.
в этом базисе.
49.
![]()
50.
![]()
51.
![]()
52.
![]()
53.
![]()
54.
![]()
Найти размерность и базис пространства решений однородной системы линейных уравнений.
55.
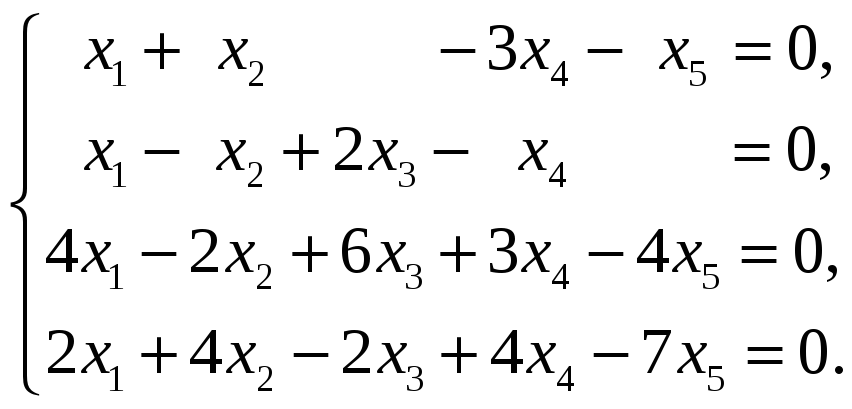 57.
57.
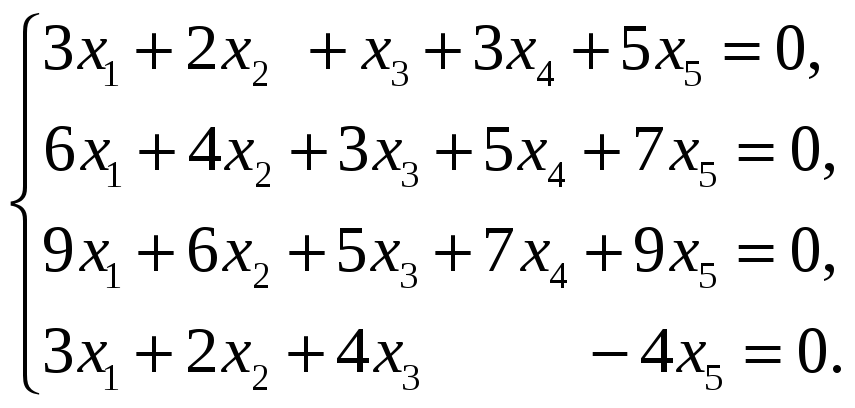
56.
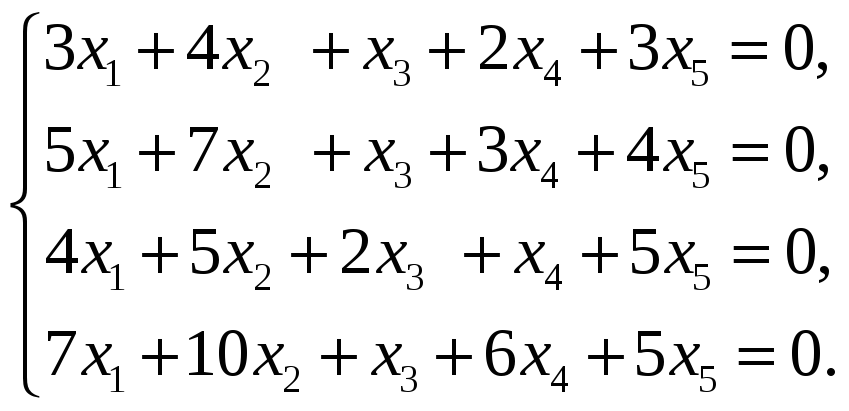 58.
58.
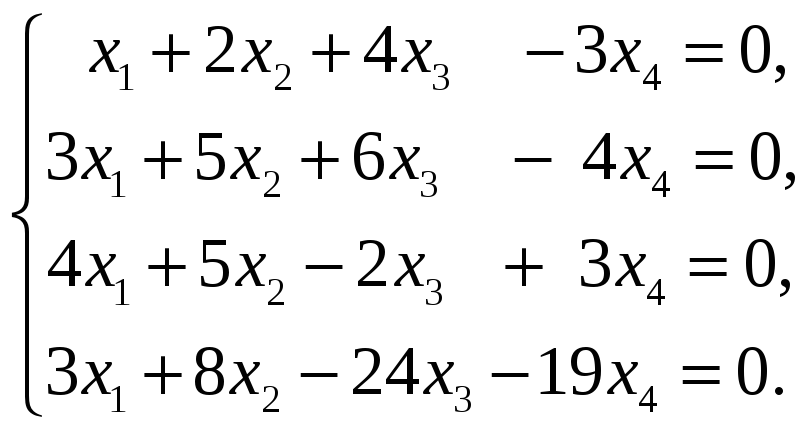
59.
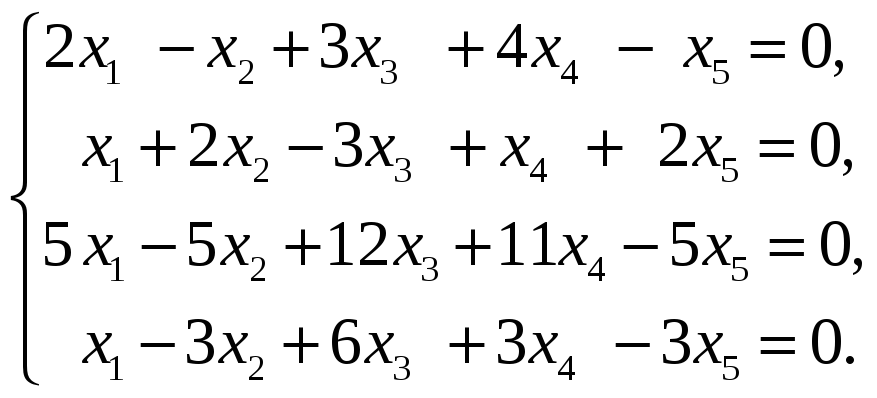 60.
60.
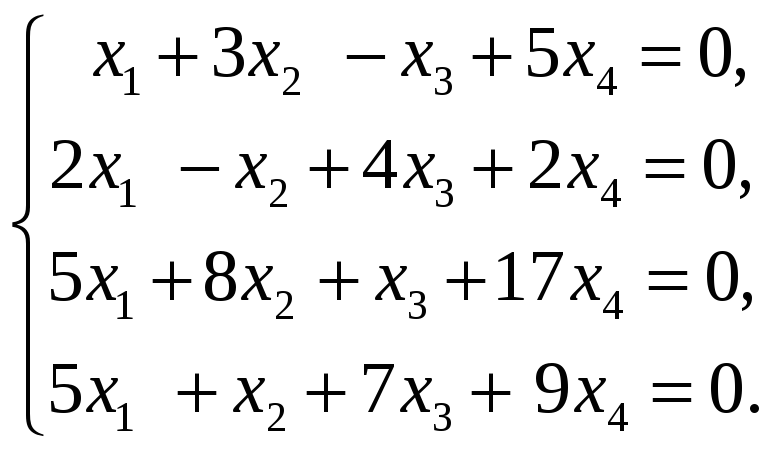
Найти базис пересечения подпространств
![]() и
и
![]() ,
натянутых на векторы
,
натянутых на векторы
![]() и
и
![]() соответственно, если все векторы заданы
своими координатами в некотором базисе
пространства.
соответственно, если все векторы заданы
своими координатами в некотором базисе
пространства.
61. 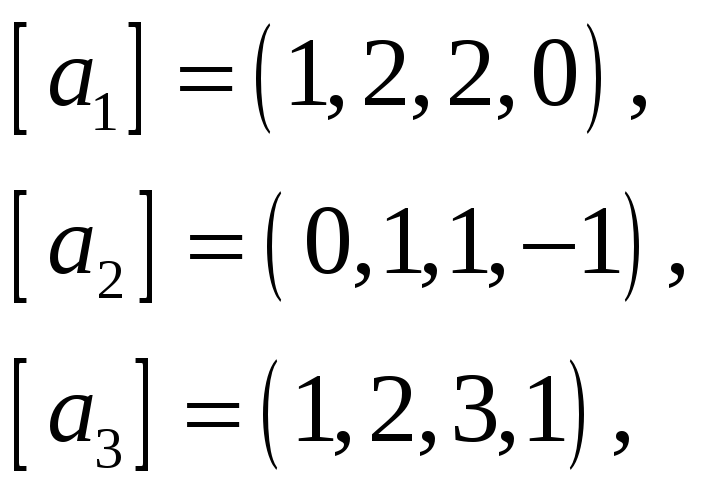
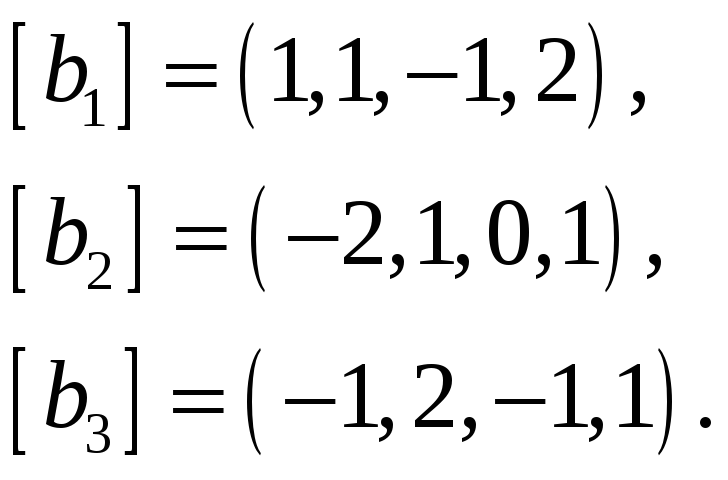
62. 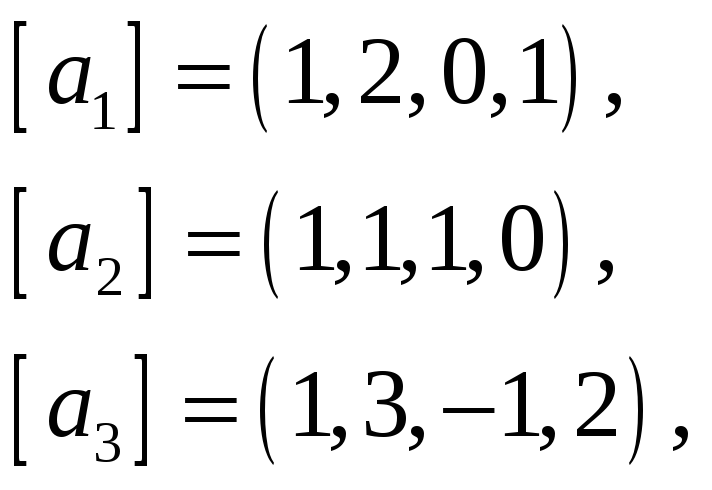
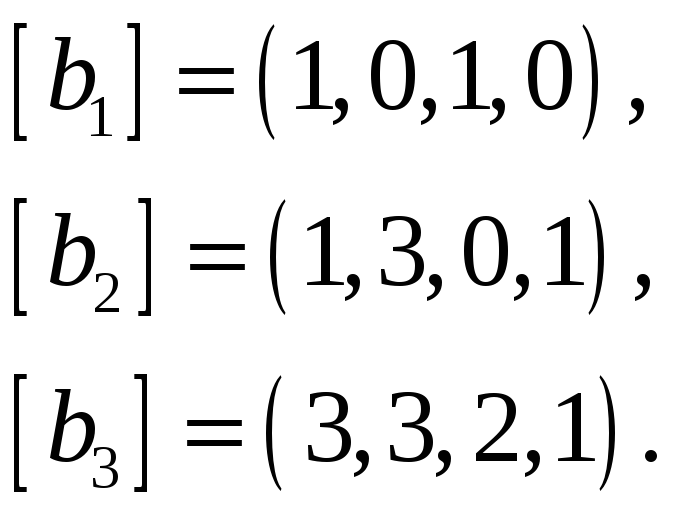
63. 
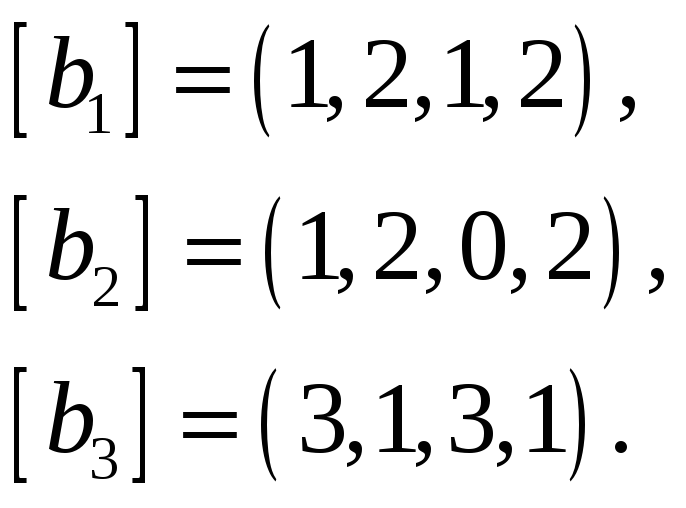
64. 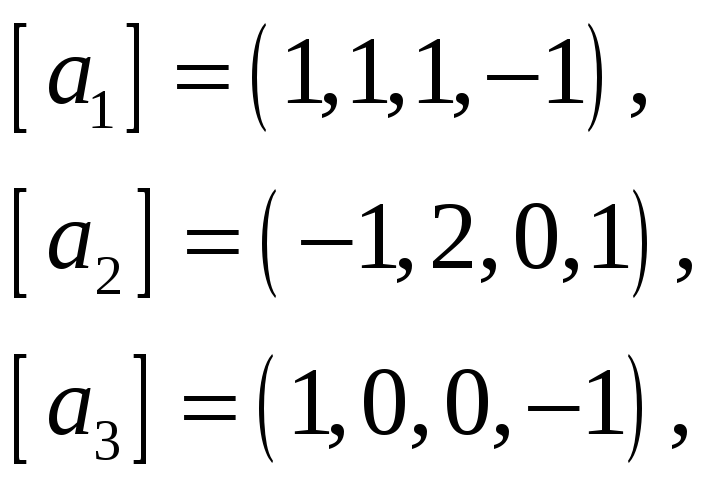
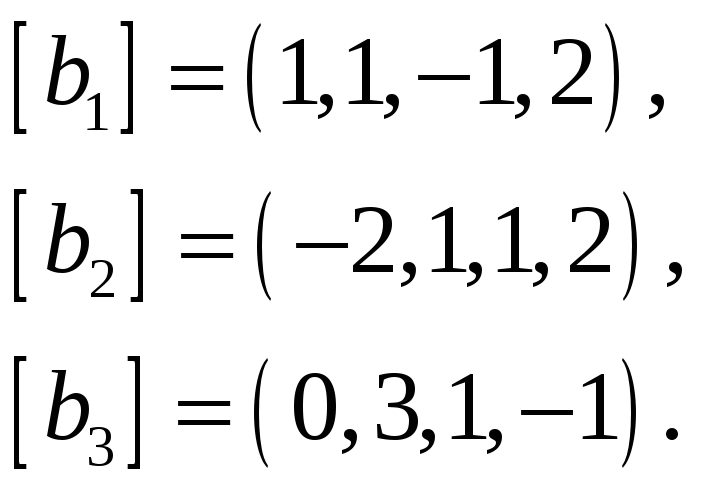
65. 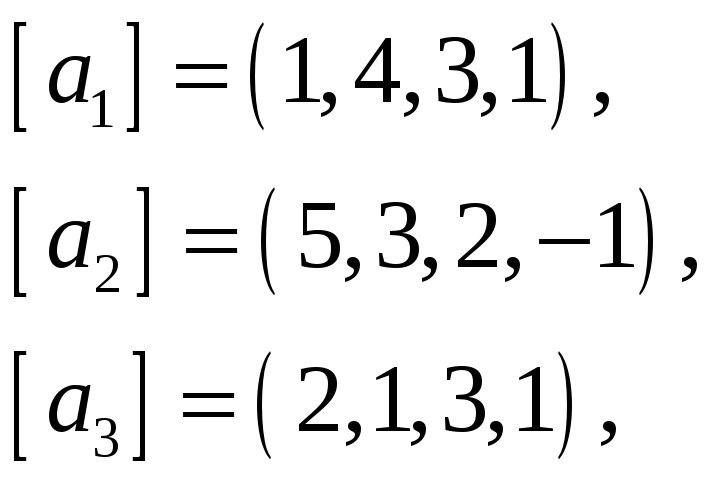
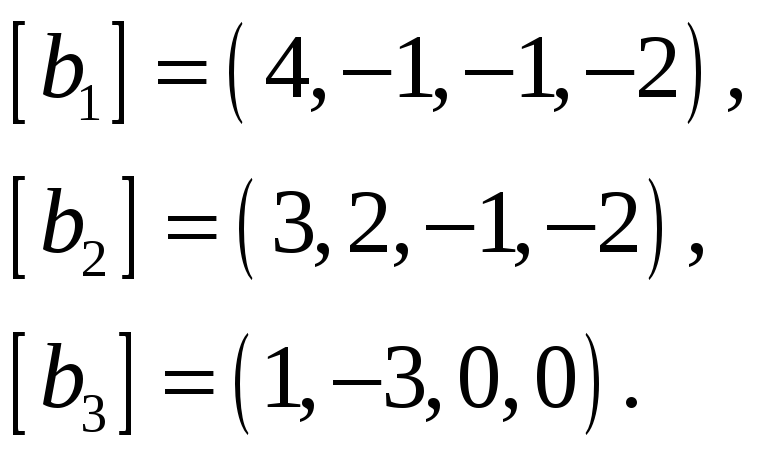
66. 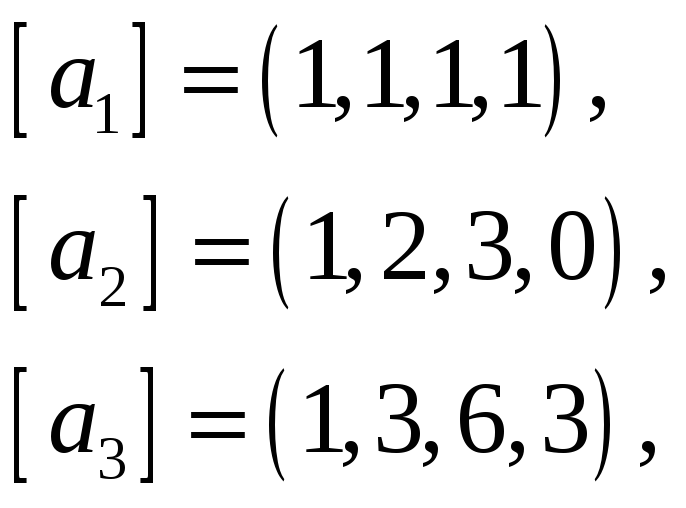
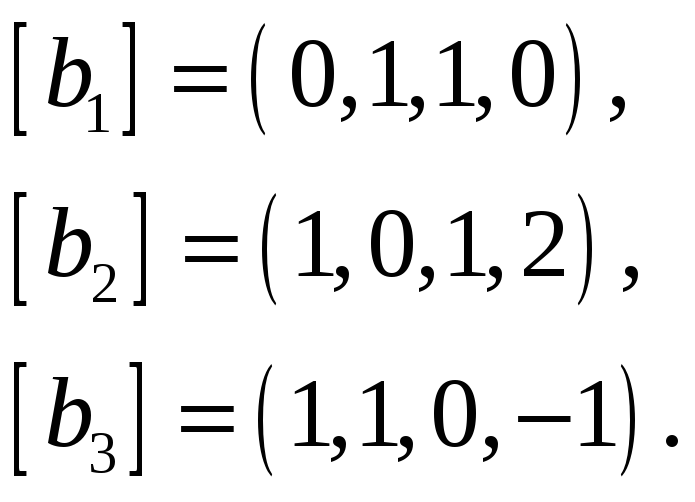
ЛИТЕРАТУРА
-
Курош А.Г. Курс высшей алгебры. 6-е изд. М., 1971.
-
Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. Часть I. Минск, 1984.
-
Милованов М.В., Толкачев М.М., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. Часть 2. Минск, 1981.
-
Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. 3- изд. М.: Наука, 1974.
Учебное издание
ЖИГОТА АЛЛА ЭДУАРДОВНА
Методические указания и контрольные работы
по курсу «Алгебра и теория чисел»
