§ I. Деление многочленов. Схема Горнера. Наибольший общий делитель.

Пусть обозначает произвольное числовое поле и — многочлены из . Многочлен называется делителем многочлена , если существует многочлен такой, что .

Теорема о делении с остатком. Для любых многочленов , существуют многочлены и такие, что , причем степень меньше степени или же . Многочлены и определены однозначно.

Многочлены и называются соответственно частным и остатком. Многочлен делит тогда и только тогда, когда .

В частном случае, когда , деление проще осуществить с помощью схемы Горнера.

Пусть . Если — частное, — остаток от деления на , то либо , либо степень равна нулю и, следовательно, .

Нетрудно видеть тогда, что коэффициенты и могут быть получены по формулам:

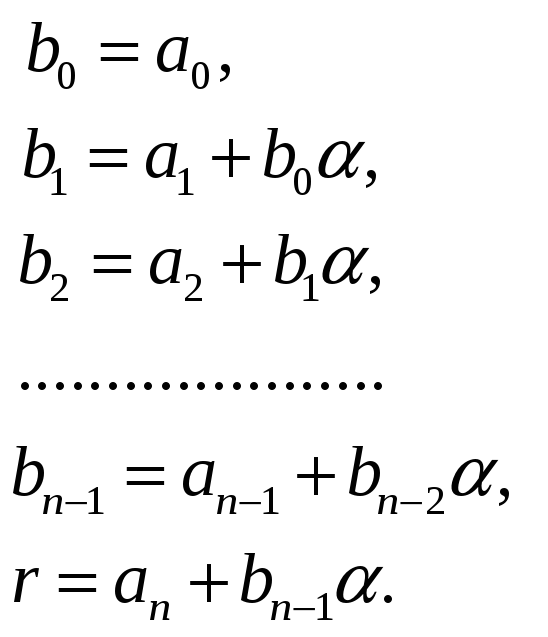(1)

Для практического использования схемы Горнера составляют таблицу. Рассмотрим пример.

Пример 1. Найти частное и остаток от деления на .

Решение. Воспользуемся схемой Горнера и составим таблицу, в первой строке которой стоят коэффициенты многочлена , а во второй записываем коэффициенты частного и остаток, вычисляя их по формулам (1):

	2	-1	0	3
2	2	3	6	15

Получаем Частное равно , остаток равен 15.

Для решения ряда задач математического анализа и алгебры бывает необходимо представлять многочлен по степеням , то есть представлять в виде: .

Для решения этой задачи используется следующий алгоритм.

Разделим на с остатком. Затем разделим частное на . Затем разделим новое частное на и т.д. Деление осуществляем до получения в частном многочлена нулевой степени:

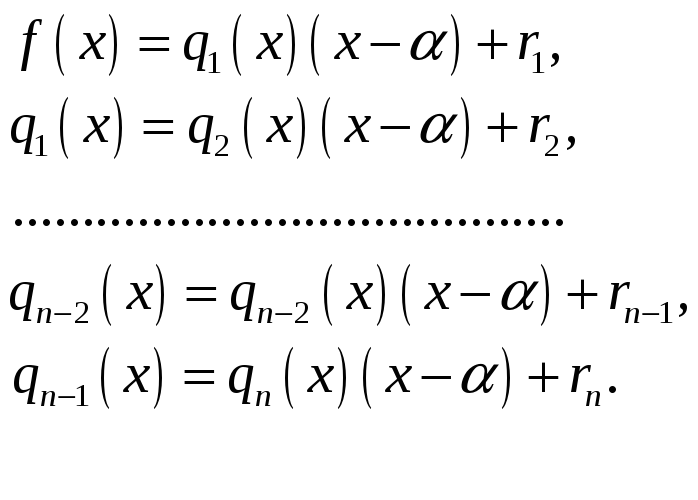(2)

Очевидно, степень равна нулю и . Подставим выражение для и выражение для : . Теперь подставим выражение для в выражение для в равенствах (2): .

Продолжая и далее этот процесс, в конечном счете получим: . Теперь ясно, что

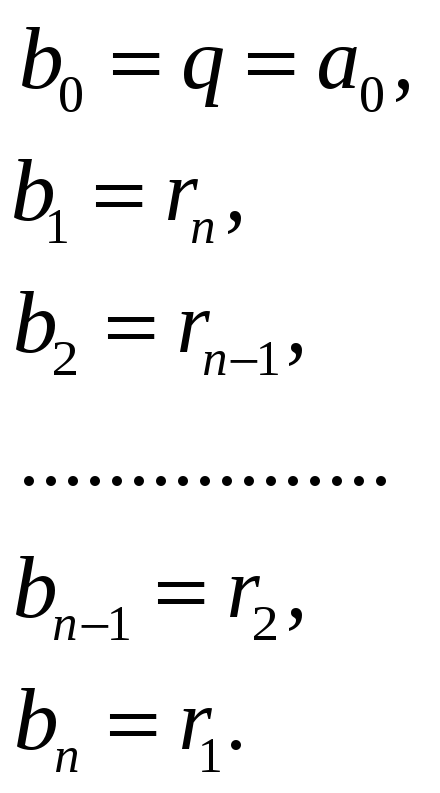(3)

Пример 2. Представить многочлен по степеням .

Решение. Для решения воспользуемся предложенным выше алгоритмом. Деление на будем осуществлять по схеме Горнера и результаты сразу записывать в таблицу:

Из формул (3) следует, что коэффициенты находятся на «ступеньках» таблицы. Получаем — искомое представление многочлена.

Представление многочлена по степеням можно использовать для вычисления значения многочлена и его производных в точке .

В самом деле, пусть

(4)

Тогда, очевидно,

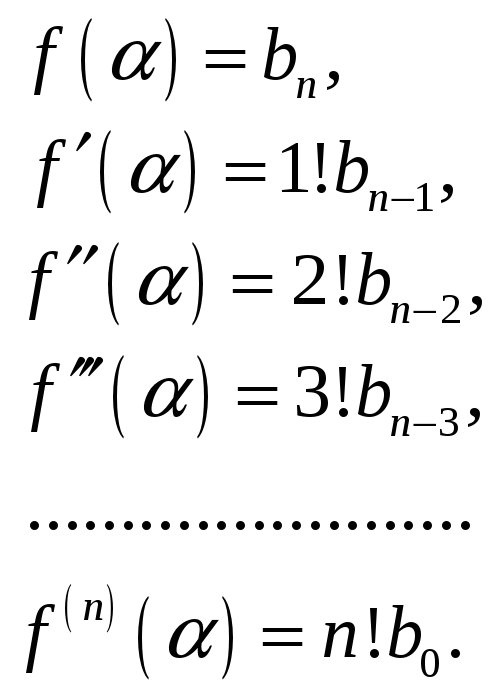(5)

Эти формулы получаются с помощью дифференцирования правой и левой частей равенства (4) или из формулы Тейлора.

Пример 3. Найти значение многочлена и всех его производных в точке .

Решение. Представим многочлен , по степеням . (См.пример 2) Тогда из формул (5) получаем

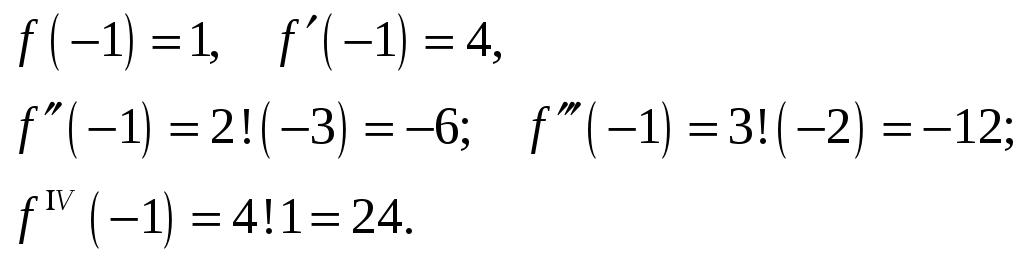
Производные более высоких порядков равны нулю.

Если — многочлены из и многочлен делит и (без остатка), то называется общим делителем и .

Наибольшим общим делителем (н.о.д.) многочленов и называется многочлен , удовлетворяющий условиям:

1) является общим делителем и ;

2) делится на всякий общий делитель и ;

3) старший коэффициент равен единице.

Для нахождения н.о.д. применяется алгоритм Евклида. Последний не равный нулю остаток в алгоритме Евклида равен н.о.д. с точностью до постоянного множителя.

Литература: — § 20, 21, — § 9.1,9.2., — № 546-551, 554-557.