§ 4. Симметрические многочлены.

Многочлен от переменных над полем называется симметрическим, если он не меняется ни при какой перестановке этих переменных. Чтобы проверить, является ли данный многочлен симметрическим, достаточно проверить, меняется ли он при перестановках любых двух из входящих в него переменных между собой.

Пример 1. Многочлен не является симметрическим, так как, если заменить в нем везде на , а — на , то получится многочлен .

Пример 2. Многочлен является симметрическим.

Симметрические многочлены от переменных

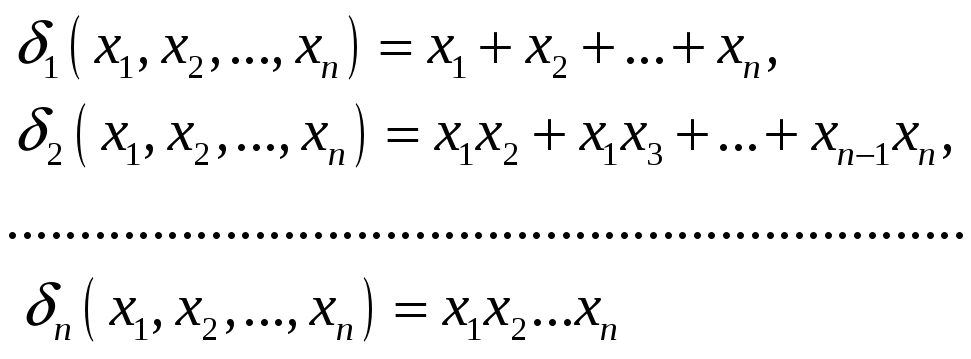
Называются основными симметрическими многочленами.

Если — многочлен от переменной над полем и — все корни (каждый корень записан столько раз, какова его кратность), то значения основных симметрических многочленов на корнях легко получаются из формул Виета:

Основная теорема о симметрических многочленах.

Всякий симметрический многочлен можно представить в виде многочлена от основных симметрических многочленов, и это представление единственно, т.е., .

Симметрический многочлен называется однородным (формой) степени , если все его члены имеют полную степень по совокупности переменных равную .

Чтобы найти выражение данного симметрического многочлена через основные, нужно сначала разбить этот многочлен на однородные части, собирая вместе все члены многочлена, имеющие одну и ту же степень по совокупности переменных. Затем выразить через основные симметрические многочлены каждую однородную часть отдельно. Чтобы выразить через основные симметрические многочлены однородный симметрический многочлен , надо взять его высший член , выписать набор показателей в нем и составить всевозможные наборы чисел вида со свойствами:

1. сумма чисел 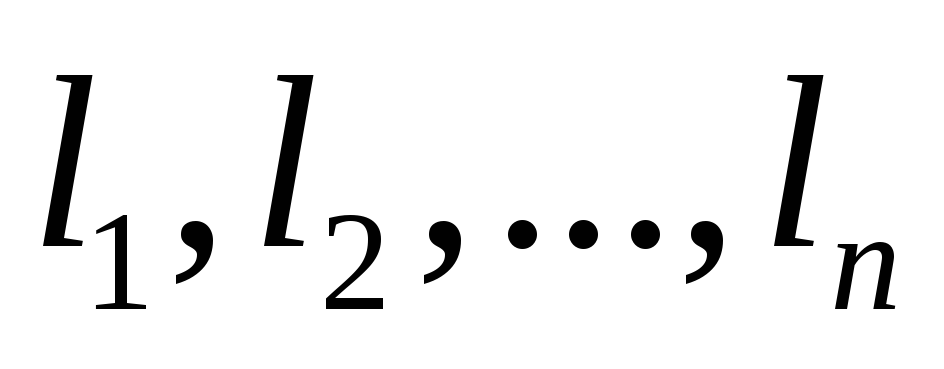в каждом наборе одна и та же и равна ;

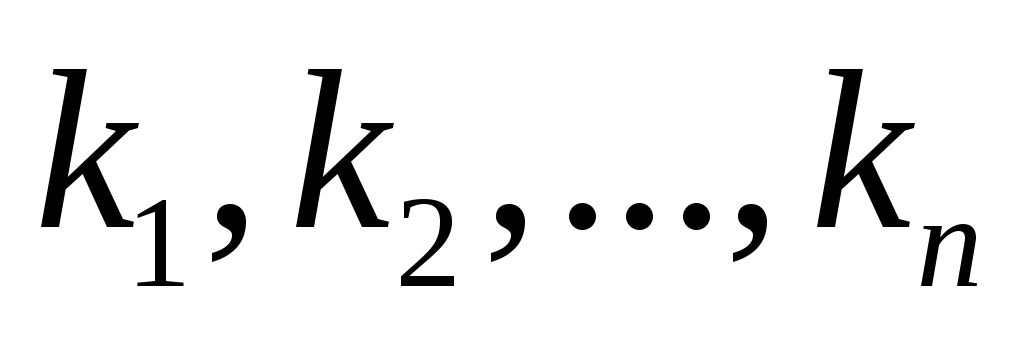2. числа каждого набора идут, не возрастая, т.е. ;

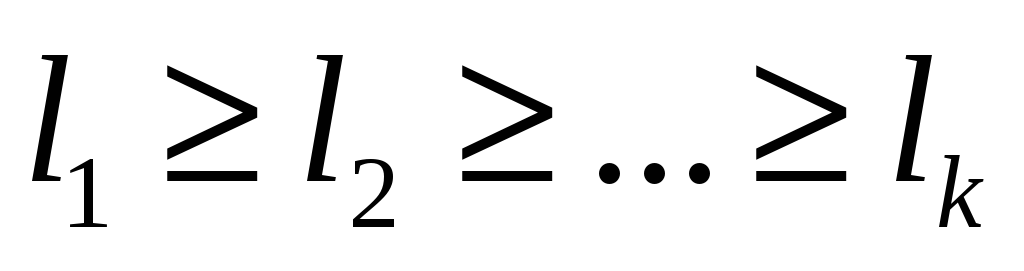3. член 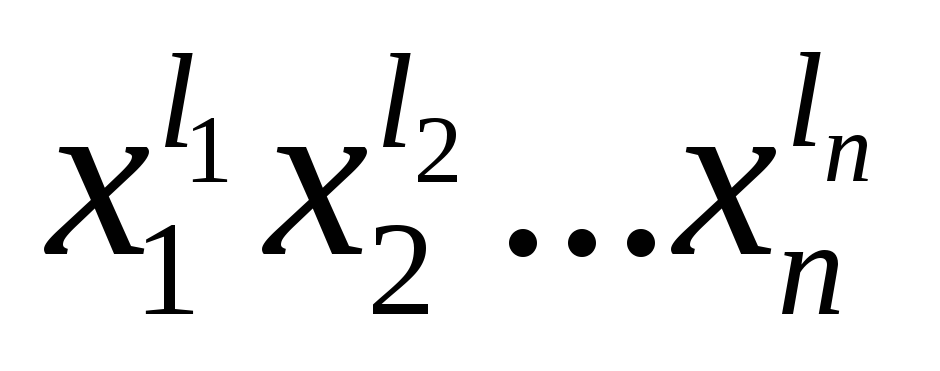не выше члена .

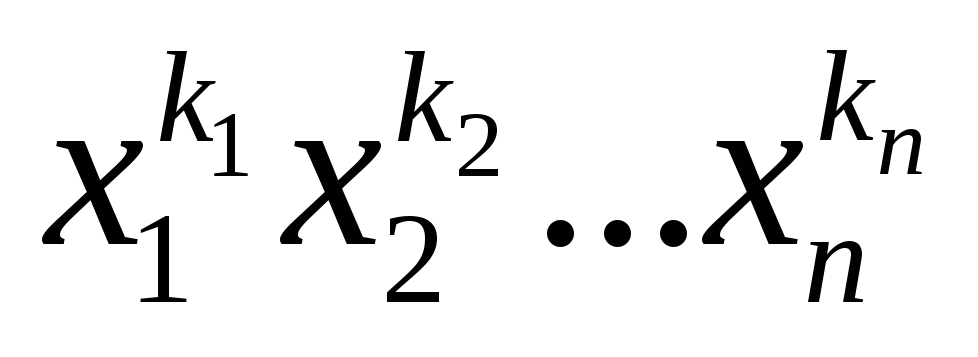После этого для каждого набора надо составить произведение и многочлен приравнять сумме построенных так произведений, взятых с неопределенными коэффициентами. Если найти эти коэффициенты, придавая различными способами численные значения переменным в обеих частях равенства, то получится выражение через основные симметрические многочлены.

Пример 3. Здесь — уже однородный симметрический многочлен, его высший член — . Составляем наборы показателей:

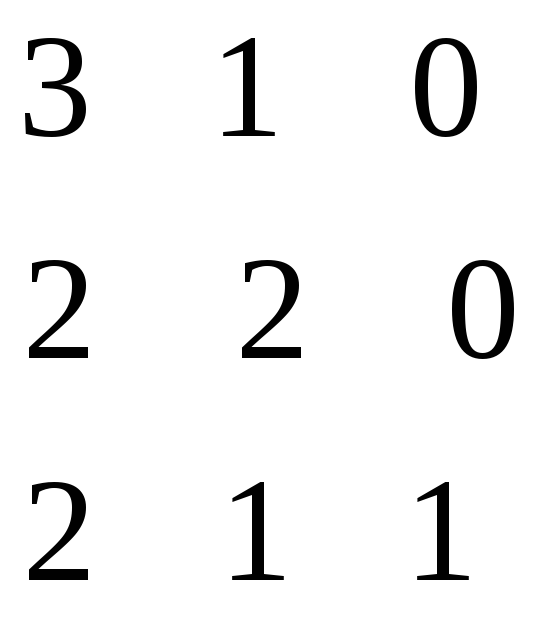
Тогда . При имеем: , , откуда . При имеем: , , откуда . .

Пример 4. .

Разбиваем на однородные части и . Для набор показателей . Это дает . Полагая , находим . Таким образом, .

Пользуясь основной теоремой о симметрических многочленах, можно найти значение любого симметрического многочлена от переменных при значениях входящих в него переменных, равных корням многочлена -ой степени от одного переменного, не зная самих этих корней.

Пример 5. Найти сумму кубов корней многочлена . Берем симметрический многочлен и выражаем его через основные симметрические. . При значениях переменных имеем . Отсюда .

Литература: — § 51, 52; — § 10.1, 10.2; — § 693-697, 699-702.