Выполнение работы на компьютерном имитаторе

1.Запустить компьютерный имитатор.

2.Ознакомиться с устройством лабораторной установки, про­смотрев демонстрационный клип.

3. Начать опыт №1. Для этого с помощью курсора мыши нажать клавишу «Приступить к опыту №1».

4. Включить электронный блок, нажав клавишу «Включить».

5. Для выбора нужного угла наклона плоскости нажать клавишу «».

6. Задать первое значение угла наклона плоскости, нажав клавишу «30°».

7.Для выбора первоначального значения угла отклонения ма­ятника нажать клавишу «».

8. Выбрать одно из возможных значений угла в диапазоне 6-10°, нажав соответствующую клавишу.

9. Для выбора значения нажать клавишу «».

10. Выбрать =2°, нажав соответствующую клавишу.

11. Пустить маятник. Для этого нажать клавишу «Запуск».

12. После появления в таблице на экране монитора значений и нажать клавишу «Сброс».

13. Повторить пп. 9-12 для 3° и 4°.

14.Повторить пп. 5-13 для углов 45° и 60°.

15.Закончить выполнение опыта №1. Выключить электронный блок, нажав клавишу «Выключить».

16. Переписать результаты опыта в тетрадь для лабораторных работ в виде табл. 1.1.

17.Нажать клавишу «Вернуться в меню».

18. По данным табл.1.1 рассчитать по формуле

средние для каждого угла значения коэффициента трения и записать их в табл.1.1.

Контрольные вопросы

1. Что такое колебания? Какие колебания называются свобод­ными затухающими?

2. Запишите дифференциальное уравнение свободных затухаю­щих колебаний и его решение.

3. Какие физические величины характеризуют свободные зату­хающие колебания? Какими формулами описываются эти величины?

4. Опишите устройство лабораторной установки.

5. Какие превращения энергии происходят в процессе колебаний наклонного маятника?

6. Выведите расчетную формулу для определения коэффициента трения с помощью наклонного маятника. Какие допущения приняты при выводе этой формулы?

7. Какие факторы влияют на погрешность определения коэф­фициента трения?

Литература

1. Трофимова Т. И. Курс физики. - М.: Высшая школа, 2003.

2. Сивухин Д.В. Общий курс физики. Т. 1. Механика. - М., 1989

3. Хайкин С.Э. Физические основы механики. — М., 1971.

4. Детлаф A.A., Яворский Б.М. Курс физики. - М., 1989.

Лабораторная работа №2

Исследование качества полированной поверхности с помощью микроинтерферометра линника

Цель работы – получение практических навыков работы с вы­со­коточным измерительным оптическим прибором и определение ка­чества полированной поверхности исследуемого образца.

Приборы и принадлежности – микроинтерферометр Линника; исследуемый образец.

Теоретическая часть Интерференция света

Интерференцией света называется явление перераспределения светового

потока в пространстве, возникающее при наложении когерентных волн, выражающееся в образовании устойчивой картины чередующихся максимумов

и минимумов интенсивности света.

Пусть волны от двух точечных источников света и одинаковой частоты и одинаковой поляризации (в этом случае можно отвлечься от векторного характера электрического поля световой волны) освещают экран (рис. 2.1).

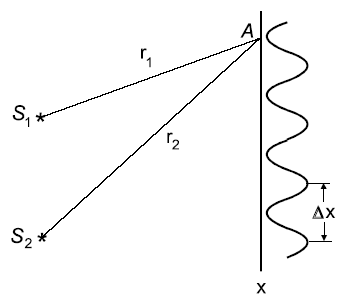
Рис. 2.1

Определим интенсивность света в некоторой точке

Электрические векторы волн в точке равны

(2.1)

где и оптические пути, пройденные волнами от источников до точки в среде с абсолютным показателем преломления волновое число; длина волны в вакууме; и амплитуды напряженностей в точке ; и начальные фазы.

Введя обозначения и (2.2) имеем

(2.3)

Амплитуду результирующего колебания легко найти с помощью векторной диаграммы, изображенной на рис. 2.2.

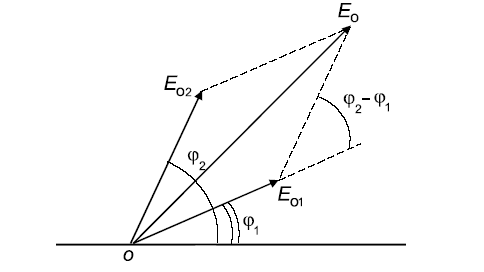
Рис. 2.2

По теореме косинусов находим

(2.4)

Учитывая, что интенсивности волн, пропорциональны квадратам их амплитуд, для интенсивности результирующего колебания получим

(2.5)

Так как в реальных источниках излучателями являются отдельные атомы, не связанные друг с другом, то разность фаз непрерывно изменяется, принимая с равной вероятностью любые значения, так что среднее по времени значение равно нулю. В этом случае интенсивность равна сумме интенсивностей складывающихся волн

(2.6)

Если же разность фаз возбуждаемых волнами колебаний остается постоянной во времени, то волны называются когерентными. Источники таких волн также когерентны. В этом случае имеет постоянное во времени, но свое для каждой точки экрана значение, в результате чего в одних местах возникают максимумы интенсивности, а в других – минимумы: наблюдается интерференционная картина.

Рассмотрим случай сложения когерентных колебаний от двух синфазных источников

При , т.е. при (где целое число 0, 1, 2... называется порядком интерференции), интенсивность результирующего колебания будет принимать максимальное значение

(2.7)

При т.е. при интенсивность результирующего колебания будет минимальной

(2.8)

Принимая во внимание обозначения (2.2), можно получить, что разность фаз

(2.9)

С учетом этого, условия возникновения максимумов и минимумов интенсивности результирующей волны можно записать в виде

если (2.10)

если (2.11)

Величина называется оптической разностью хода.

Таким образом, суммарная интенсивность зависит от точки наблюдения. На экране будут наблюдаться светлые и темные интерференционные полосы. Интенсивность периодически изменяется вдоль оси от до Пространственный период изменения интенсивности называется шириной

интерференционной полосы (рис.2.1).