Обоснование закона падения дебита нефти

Универсальный закон падения дебита нефти скважины в период постепенного увеличения в продукции воды или газа при разработке пласта с заводнением или на естественном режиме впервые установлен Р.И. Медведским в 1987 году [4] на основе трех предположений, а именно:

Функциональная связь между входным и выходным параметром некоторого процесса имеет физический смысл, если эти параметры объединены в безразмерные комплексы.

Функциональная связь не должна зависеть от произвола в выборе начала отсчета времени.

Вид функциональной зависимости остается неизменным при учете баланса массы вещества.

Для обоснования универсального закона падения дебита скважины по нефти при обводнении допустим, что скважина эксплуатирует изолированную извне зону пласта, активные потенциально извлекаемые запасы которой к началу эксплуатации равны . В ходе эксплуатации дебит скважины по нефти падает от начального до текущего . Допуская зависимость одного безразмерного комплекса от другого в виде функции:

,

(1.13)

легко показать, что функция должна обладать следующими свойствами:

Если дебит по жидкости после обводнения остается неизменным, то по физическому смыслу соответствует накопленному объему добытой жидкости, которую обозначим и тогда последнюю формулу можно переписать так:

.

При переменном дебите по жидкости объем накопленной жидкости растет строго монотонно и поэтому его можно использовать в качестве аналога времени и если провести все выкладки заново можно получить общую зависимость:

.

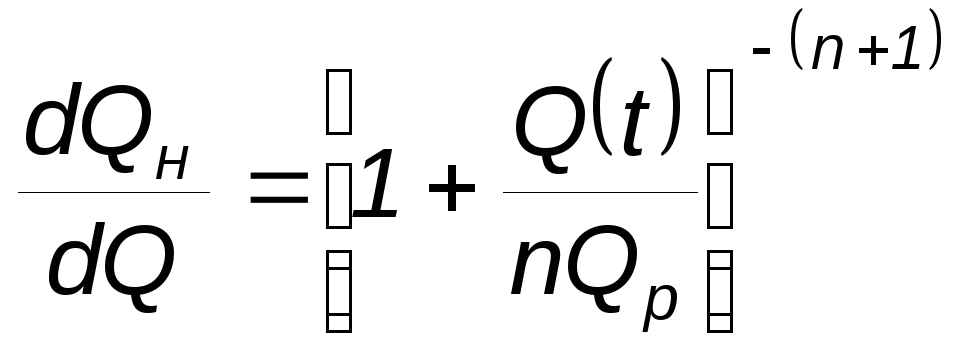Поскольку , то для дебита по нефти получаем формулу:

,

(1.23)

а для накопленной добычи

.

(1.24)

Обобщенная характеристика вытеснения

Зависимость типа (2.10), связывающая накопленную добычу нефти из пласта с накопленной добычей жидкости и вытекающая из теории Баклея-Леверетта при целом ряде допущений (а именно, однородности пласта и переноса закономерности отмывки с конечного этапа на весь процесс с начала его осуществления) тем не менее широко используется на практике, в том числе для слоистых пластов, и позволяет получать вполне приемлемые результаты в прогнозе добычи нефти. Это означает, что некоторые из этих ограничений могут быть сняты при соответствующем обобщении зависимости (2.10).

(2.10)

Покажем, как вывести эту обобщенную зависимость на основании исходной, сняв только ограничения на ее применимость для больших . При малых она уже неприемлема, а для вообще дает абсурдный результат в правой части при конечном значении в левой. Для того, чтобы сделать (2.10) пригодной и для малых , укажем, что без нарушения ее поведения при больших она может быть представлена в виде:

при любой положительной величине . Полагая , находим отсюда:

.

(2.11)

Дифференцируя (2.11), получаем

.

(2.12)

Замечая, что производная соответствует интенсивности отбора нефти в момент времени , а соответствует интенсивности отбора жидкости, получим:

.

(2.13)

При имеет место равенство и поскольку , то из (2.13) следует, что , то есть , а также

.

(2.14)

Напомним, что величина соответствует потенциально извлекаемым из пласта запасам, которые лучше обозначить .

Интегрируя (2.14) по времени, найдем равенство

,

(2.15)

которое заменой обозначений приводится к (2.10).

Заметим, что , как и , являются функциями времени, что для упрощения в (2.15) не отмечено.

Зависимость (2.15) является обобщением (2.10) и в отличии от нее не теряет смысла при , при котором переходит в широко используемую экспоненциальную зависимость:

,

(2.16)

которая при постоянном темпе отбора с учетом этого накопленный отбор жидкости , и выражение (2.16) преобразуется к виду:

.

(2.17)

Экспоненциальная зависимость (2.17) широко использовалась Э.А. Мухарским совместно с В.Д. Лысенко [1] для проектирования разработки месторождений. При этом принимался равным начальному дебиту скважин. Накопленный отбор с момента ввода скважины в эксплуатацию определялся по формуле (2.17), а накопленная добыча по месторождению определялась суммированием отборов по каждой скважине с учетом разновременности их ввода в работу.

Зависимость (2.15), полученная здесь на основании одного из выводов теории Баклея-Леверетта, полностью совпадает с зависимостью универсального закона, выведенной ранее для одиночной скважины, что не удивительно, поскольку ни в одном из допущений, положенных в основу вывода универсального закона, нет ссылки на геометрию течения и число скважин. Отсюда следует, что в этой части универсальный закон является обобщением этой теории.
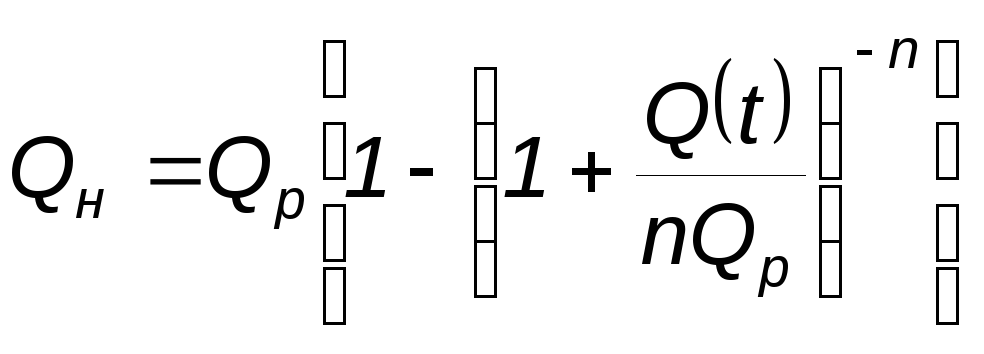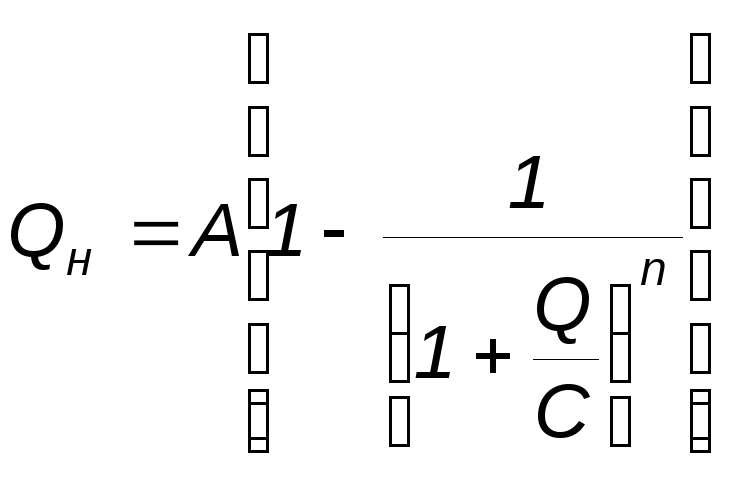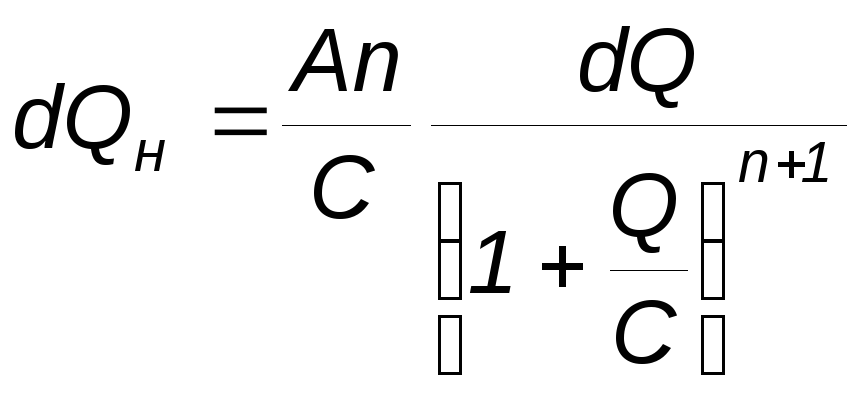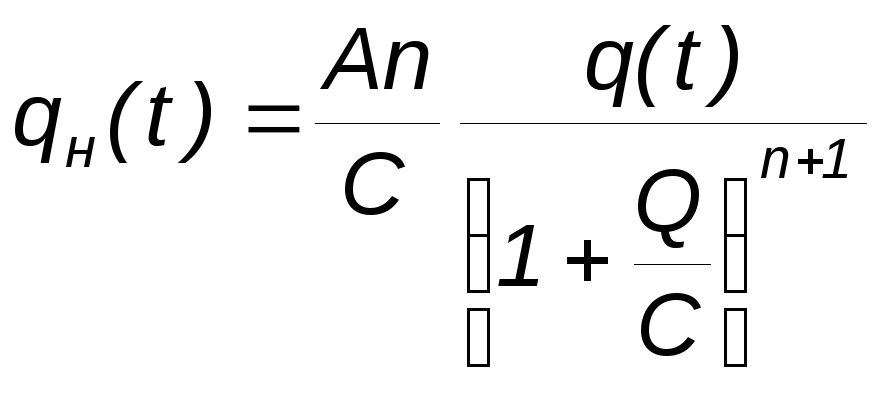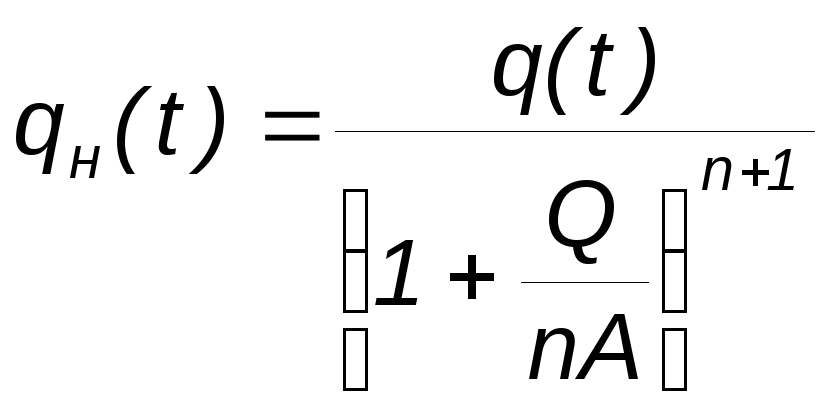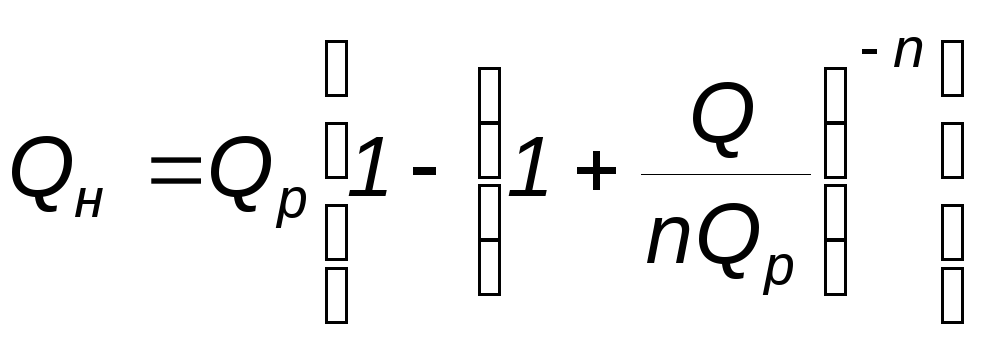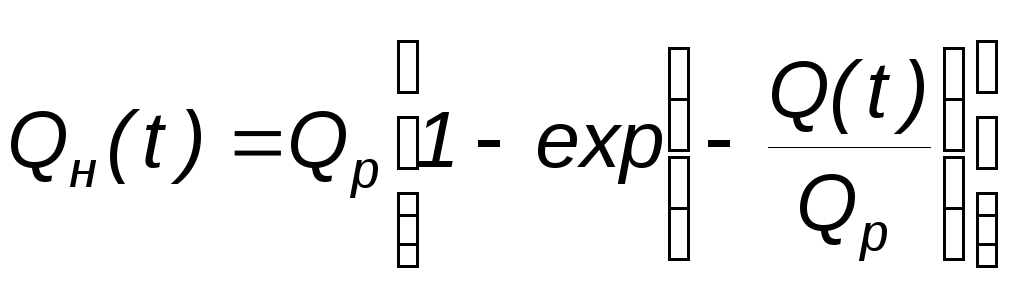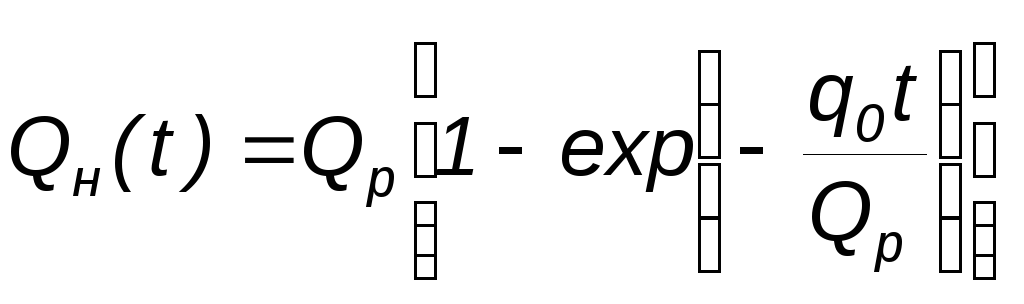