Оценка упругого запаса законтурной воды в исследования ван эвердингена и херста

Теория упругого режима фильтрации жидкости в нефтяных коллекторах зародилась при попытках объяснения замедленной реакции скважин на остановку или пуск соседних на месторождении Ист Тексас в начале 30–х годов. Вскоре после того как на нем впервые в практике нефтедобычи начали нагнетать воду с начала для сброса подтоварной воды, а затем после того как было замечено повышение пластового давления и рост дебита добывающих скважин, заводнение стали проводить целенаправленно в качестве вторичного метода воздействия на пласт.

Первые шаги в исследовании упругого режима на данном месторождении описаны в книге М.Маскета и более подробно в книге В.Н. Щелкачева. В конце 40-х годов когда добыча нефти на этом крупнейшем месторождении США стала падать возникла необходимость во вводе в эксплуатацию соседних сними мелких месторождений-спутников. Разрабатывались они при режиме растворенного газа. Применение метода материального баланса к фактическим данным показало увеличение начальных запасов на этих месторождениях, что сначала Херстом, а затем и совместно с Ван Эвердингеном было объяснено вторжением законтурной воды. Для оценки объема вторгшейся воды эти авторы уподобили залежь укрупненной скважине (по терминологии В.Н. Щелкачева), к которой из окружающей водоносной зоны подтекает вода. Поскольку эта зона бесконечная, то приток воды может быть оценен только в рамках нестационарного упруговодонапорного режима.

Для того, чтобы изложить метод Ван Эвердингена и Херста и предложить его развитие, дадим сначала простой вывод уравнения нестационарной фильтрации малосжимаемой жидкости в трубке тока переменного сечения.

Пусть отсчет координаты ведется вдоль оси трубки тока в направлении роста давления и означает площадь поперечного сечения и величину расхода в координате - по закону Дарси:

Выделим сечение и элементарный объем поперек трубки тока. За время в следствие понижения давления и сопутствующего ему расширения жидкости и сжатия скелета породы в объеме в трубке тока выделится количество жидкости:

, где

вместе с втекающим в элемент объемом этот объем выводится через сечение с расходом при этом баланс жидкости:

.

Поскольку:

,

Отсюда:

.

Для плоскорадиального течения , :

. (1)

Обезразмеривание приводит к уравнению:

, , .

Данное уравнение по предложению В.Н Щелкачева получило название уравнения пьезопроводность по аналогии с ранее предложенным уравнением теплопроводности. Последнее было впервые выведено основоположником теории теплопроводности Ж.Б. Фурье в начале 19-20 века. Почти каждая задача теории упругого режима фильтрации имеет аналог в теории теплопроводности, различие состоит только в иной интерпретации процесса.

В приложениях теории упругого режима к практическим задачам разработки особая роль принадлежит следующим задачам.

Задача 1: скважина в бесконечном пласте с начальным давлением вводится в работу с постоянным противодавлением .

Эта задача для нормированной функции давления:

сводится к решению уравнения теплопроводности:

,

со следующими граничными и начальными условиями:

;

.

Решение задачи, полученное Ван Эвердингеном и Херстом, таково:

.

Здесь и ниже , - функции Бесселя, порядок которых указан индексом.

Г. Карслоу и Д. Егер в своей фундаментальной монографии указывают, что аналитическое решение данной краевой задачи впервые было найдено Никольсоном в 1921 г почти за 30 лет до Ван Эвердингена и Херста. Однако последнее не только вывели аналитическое решение в виде интеграла от бесселовых функций, но составили подробные таблицы, поскольку к тому времени уже появились быстродействующие вычислительные машины.

В приложении важно не столько поле давления вокруг скважины, сколько приток жидкости к ней, который задается выражением:

,

где .

Э.Б. Чекалюк из эвристических соображений получил для этой функции простое приближение, которое мало отличается от табличных значений:

.

Долгое время он считал эту функцию точным решением. Однако это не так, что можно просто доказать сравнением асимптот точной и приближения для нее при :

.

Однако легко видеть, что для .

Таким образом, точность приближения Э.Б.Чекалюка состоит в том, что асимптотически совпадает с точным как при так и при .

Задача 2: скважина вводится в работу в первоначально невозмущенном пласте с постоянным дебитом . Необходимо найти распределение давления в пласте и давления на контуре укрупненной скважины.

Задача 2 для функции сводится к решению уравнения теплопроводности при следующих граничных и начальных условиях:

.

Ван Эвердинген и Херст для понижения давления на контуре скважины получили выражение:

где .

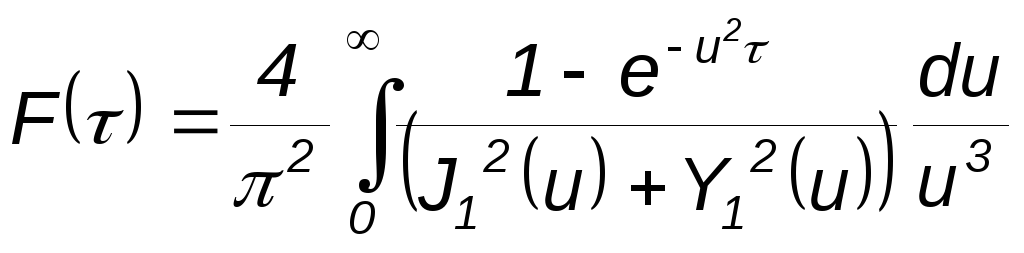Это решение названными авторами затабулировано.

Р.И. Медведский указал для этой функции приближение:

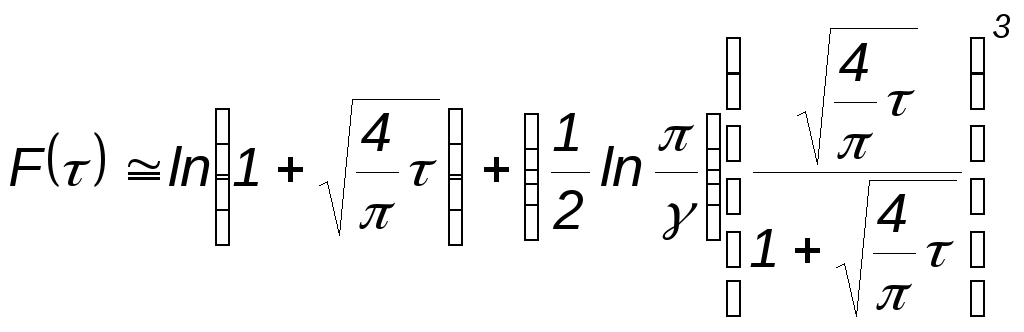
Асимптотически оно совпадает с точным как для малых так и для больших . Погрешность этой функции как установлено многочисленными проверками с табличными данными, полученными Ван Эвердингеном и Херстом, не превышает 2%, так что оно вполне приемлемо для практических целей.

Решения, полученные Ван Эвердингеном и Херстом, широко используется для прогноза показателей разработки нефтяных и газовых месторождений при активной водоносной зоне.

Замена залежи укрупненной скважиной, предложенное Ван Эвердингеном и Херстом, было шагом вперед, при этом не учитываются процессы происходящие внутри залежи, а именно:

• одновременно с подтоком воды из-за контура, нефть к скважинам вытесняется вследствие расширения поровой жидкости и сжатия скелета породы.

• пластовое давление в залежи не равно давлению на контуре залежи.

Следовательно, для увеличения точности предложенного Ван Эвердингеном и Херстом подхода следует учесть упругость пласта в пределах залежи и внутренние фильтрационные сопротивления при течении нефти к скважинам.

Лектор: Севастьянов А.А., канд.тех.наук

1