Курс лекций по разработке нефтяных месторождений (для студентов ТюмГНГУ, специальности РЭНМ) Часть 2. Предварительная редакция

ОБОСНОВАНИЕ ДЕБИТОВ ЖИДКОСТИ В УСЛОВИЯХ ЖЕСТКО ВОДОНАПОРНОГО РЕЖИМА 2

Оценка дебитов при однорядной системе размещения скважин 2

Оценка дебита для элемента пятиточечной системы разработки 3

Оценка дебита для элемента семиточечной системы разработки 4

Оценка дебитов при трехрядной системе размещения скважин 5

О ЗАВИСИМОСТИ ДЕБИТА СКВАЖИН ОТ ВРЕМЕНИ 7

Обоснование закона падения дебита нефти 8

Обобщенная характеристика вытеснения 9

ТЕОРИЯ БАКЛЕЯ И ЛЕВЕРЕТТА. 10

Смешанное вытеснение нефти водой. 10

МОДЕЛИ ПОРШНЕВОГО ВЫТЕСНЕНИЯ НЕФТИ ВОДОЙ В УСЛОВИЯХ СЛОИСТО-НЕОДНОРОДНОГО ПЛАСТА 13

Модель Стайлса 13

Метод Дикстра и Парсонса. 14

ПРИМЕР РАСЧЕТА ОСНОВНЫХ ПОКАЗАТЕЛЕЙ РАЗРАБОТКИ В ГОСПЛАНОВСКОЙ ФОРМЕ 17

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ УПРУГО РЕЖИМА 22

ОПРЕДЕЛЕНИЕ УПРУГОСТИ РЕЖИМА; ОБЪЕМНАЯ УПРУГОСТЬ НЕФТИ, ВОДЫ И ПЛАСТА 22

§ 1. Определение и наиболее характерные проявления упругого режима 22

§ 3. Объемная упругость пласта; учет совместного влияния упругости пласта и насыщающей его жидкости 29

§ 4. Коэффициент пьезопроводности пласта и основные безразмерные параметры теории упругого режима 33

§ 5. Замечания по поводу постановки основных задач теории упругого режима 34

ИССЛЕДОВАНИЕ НЕУСТАНОВИВШИХСЯ ПРОЦЕССОВ, ВЫЗВАННЫХ ПУСКОМ ИЛИ ОСТАНОВКОЙ СКВАЖИНЫ В ПРОСТЕЙШИХ УСЛОВИЯХ УПРУГО-ВОДОНАПОРНОГО РЕЖИМА 35

§ 1. Вводные замечания 35

§ 4. Особенности изменения формы пьезометрической воронки депрессии после остановки возмущающей скважины или после ее пуска с постоянным дебитом 37

§ 5. Перераспределение пластового давления и изменение дебита возмущающей скважины после ее пуска с постоянным забойным давлением 41

МЕТОД СУПЕРПОЗИЦИИ И ЕГО ИСПОЛЬЗОВАНИЕ ПРИ РЕШЕНИИ ЗАДАЧ ВЗАИМОДЕЙСТВИЯ СКВАЖИН И ПРИ УЧЕТЕ ВЛИЯНИЯ ИЗМЕНЕНИЯ ТЕМПА ДОБЫЧИ ЖИДКОСТИ ИЗ НИХ 45

§ 1. Общие замечания о методе суперпозиции 45

§ 2. Учет влияния остановки или изменения темпа добычи возмущающей скважины 46

ОЦЕНКА УПРУГОГО ЗАПАСА ЗАКОНТУРНОЙ ВОДЫ В ИССЛЕДОВАНИЯ ВАН ЭВЕРДИНГЕНА И ХЕРСТА 47

Обоснование дебитов жидкости в условиях жестко водонапорного режима Оценка дебитов при однорядной системе размещения скважин

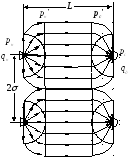
Для легкости восприятия примем фильтрующиеся жидкости цветными, то есть фазовые проницаемости, динамические вязкости для нефти и воды равны

Приводимые далее выражения справедливы при условии, что .

Внутренние сопротивления при течении жидкости вблизи нагнетательной скважины рассчитываются при условии, что плоско-радиальный поток сменяется плоско-параллельным на удалении от скважины . Это получается из предположения, что полупериметр окружности обращенной вовнутрь элемента равен расстоянию между скважинами в ряду, то если формирующемуся прямолинейно-параллельному фронту вытеснения

Таким образом, внутренние фильтрационные сопротивления вблизи нагнетательной скважины при условии плоско-радиального течения будут равны:

Внешние фильтрационные сопротивления между рядом нагнетательных скважин и первым рядом добывающих скважин будут равны

где

Внутренние сопротивления вблизи добывающих скважин первого ряда при изменении типа течения жидкости

Перепишем выражения для потерь давления

.

При условии движения реальных жидкостей в выражении изменятся фильтрационные сопротивления учитывающие динамические и фильтрационные свойства фаз, а также положение фронта вытеснения нефти водой.

Оценка дебита для элемента пятиточечной системы разработки

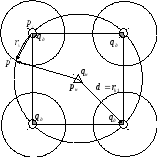
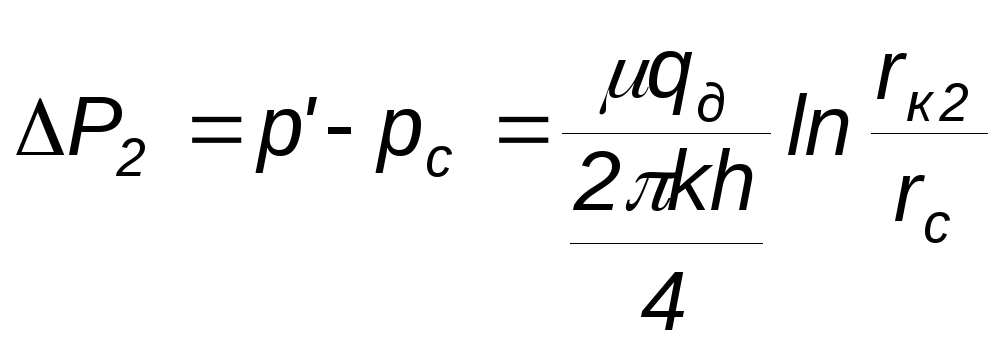
если принять , и

Оценка дебита для элемента семиточечной системы разработки

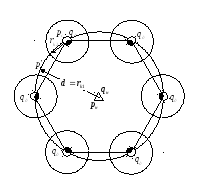
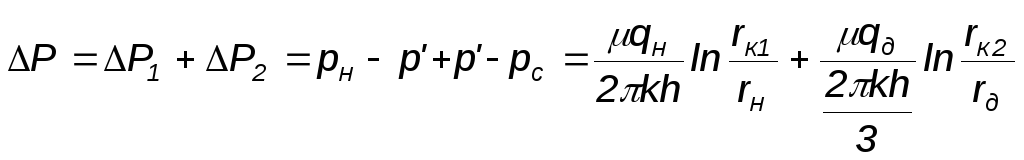
если принять , , также можно получить формулу для обоснования дебита исходя из условия

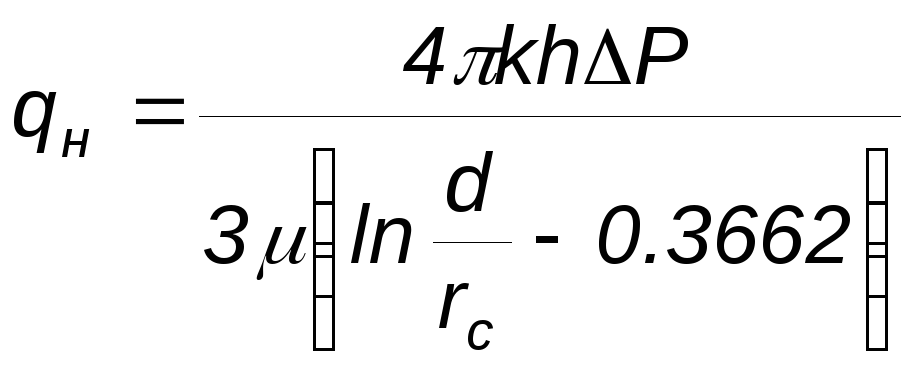
Оценка дебитов при трехрядной системе размещения скважин

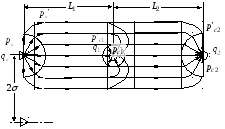
Приводимые далее выражения справедливы при условии, что .

Внутренние сопротивления при течении жидкости вблизи нагнетательной скважины рассчитываются при условии, что плоско-радиальный поток сменяется плоско-параллельным на удалении от скважины . Это получается из предположения, что полупериметр окружности обращенной вовнутрь элемента равен расстоянию между скважинами в ряду, то если формирующемуся прямолинейно-параллельному фронту вытеснения

Внешние фильтрационные сопротивления между рядом нагнетательных скважин и первым рядом добывающих скважин будут равны

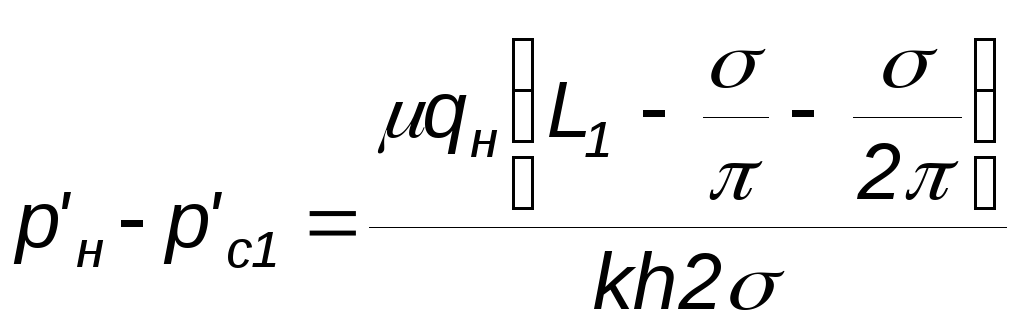
Внутренние сопротивления вблизи добывающих скважин первого ряда при изменении типа течения жидкости равны:

при условии, что или

Внешние сопротивления при течении жидкости между первым и вторым (стягивающим) рядами

Внутренние сопротивления вблизи добывающих скважин второго ряда при изменении типа течения жидкости

Перепишем выражения для потерь давления

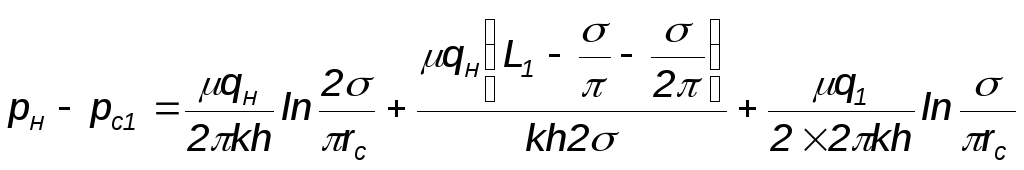
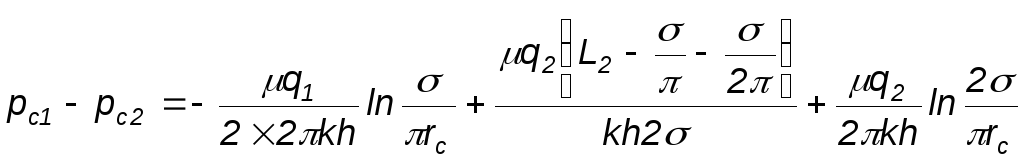
Для определения дебита скважин каждого ряда необходимо решить систему уравнений:

(1)

(2)

(3)

где ;

;

.

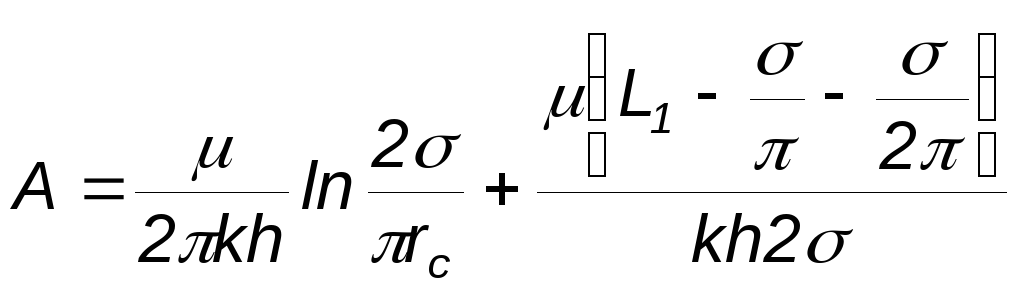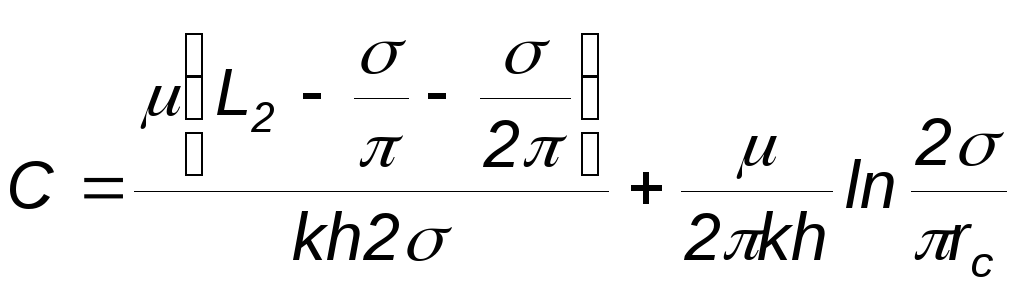Выразим из первого уравнения подставляя вместо выражение (3):

таким образом, равен:

(4)

Выразим из второго равенства

(5)

приравняем выражения (4) и (5)

и выразим

зная используя выражение (4) определим

О зависимости дебита скважин от времени

Промышленная добыча нефти началась задолго до того, как было установлено, что фильтрация нефти в пласте подчиняется законам подземной гидравлики. Тем не менее, необходимо было с открытием каждого месторождения решать важные задачи, такие как: следует ли на данном месторождении бурить следующую скважину, вкладывать деньги в обустройство месторождения и строительство нефтепровода. Эти и многие другие вопросы упирались в прогнозирование добычи нефти со скважины или их группы. При отсутствии теории прогноз проводился на основании обобщения опыта работы ранее пробуренных скважин. При большом их числе и длительном сроке работы необходимо было пользоваться методами статистики. Так, было установлено, что по большинству скважин, режим работы которых не нарушается частыми ремонтами, логарифм дебита нефти изменяется по отношению к первоначальному пропорционально времени, то есть:

.

(1)

Отсюда потенцированием получаем:

.

(2)

Такой вывод был сделан в работах американских инженеров С. Била и Х. Льюиса, а также бакинца С.И.Чарноцкого.

Аналогичная формула закона падения дебита во времени для скважины, эксплуатирующей залежь в режиме растворенного газа, получена теоретически С.Л.Лейбензоном в 1923 году в период его работы в Баку. В то время разработка всех месторождений велась на истощение, для добычи нефти из скважин применяли компрессорный газлифт. Компрессорные станции были тогда вместе с деревянными вышками характерными элементами промыслового пейзажа. Благодаря газлифту добыча на истощение велась долгие годы.

В последующем при разработке месторождений с закачкой воды было установлено, что падение дебита нефти по закону (2) характерно и в условиях прогрессирующего обводнения скважин. Такое положение было обосновано в работах Э.Б. Мухарского, В.Д. Лысенко [1] и И.Г.Пермякова [2], сделавших свои выводы на основе многочисленных данных по разработке нефтяных месторождений Урало-Поволжья (Башкортостан, Татарстан, Самарская и Саратовская области). Особенно много для популяризации закона (2) сделали В.Д. Лысенко и Э.Б.Мухарский, которые связали декремент (быстроту) затухания с потенциально извлекаемыми запасами скважины.

А именно, интегрируя (2) от 0 до получаем выражение для накопленной добычи:

.

(3)

При накопленная добыча, если снять экономические ограничения, стремится к потенциально возможной , тогда из (3) находим:

(4)

и (3) можно записать в виде:

,

(5)

которую широко использовали В.Д. Лысенко и Э.Б.Мухарский для расчета дебита скважин при проектировании разработки месторождений. Она же вошла в методику Госплана СССР.

В США одновременно с познанием законов подземной гидромеханики благодаря основополагающим работам М. Маскета не утратили интереса к статистическим зависимостям типа (1, 2), тем более, что в США период разработки месторождений на истощение из-за применения газлифта значительно длиннее, чем в нашей стране. В 1945 году Дж. Арпс [3] подверг статистической обработке материал по большому числу скважин с начала прошлого века, в результате чего было установлено, что темп падения дебита нефти связан с его текущей величиной зависимостью типа:

,

(6)

где и - неотрицательные постоянные, а (6) представляет собой уже дифференциальное уравнение. При этому уравнению удовлетворяет функция (3), поэтому выведенная Арпсом зависимость приводит к более общим формулам, чем (5).

Уравнение Арпса (6), судя по публикациям, применяется в США для оценки коммерческой ценности малых месторождений.

Зависимость (6), хотя и проверена на работе нескольких тысяч скважин, может быть всего лишь случайной находкой и на следующей тысяче скважин может не подтвердиться. Ситуация здесь примерно такая же, как в бросании жребия с использованием монеты – многократное выпадение одной стороны не гарантирует такого же исхода при следующем бросании.

Теоретическое обоснование зависимости (6), было сделано Р.И.Медведским в 1987г. и приводится в следующем параграфе.