-
Асимптоты графика функции: вертикальная, горизонтальная, наклонная. Геометрический смысл наклонной асимптоты.
ОПР1: Прямая x = X0 называется вертикальной асимптотой графика функции Y=f(x), если хотя бы одно из предельных значений lim f(x) или lim f(x) при x X0+ или X0- равно + или -.
ОПР2: Прямая y = A называется горизонтальной асимптотой графика функции Y=f(x) при x+ (x -) если lim f(x) =A.
ОПР3: Прямая Y=k x + b (k 0) называется наклонной асимптотой графика функции Y=f(x) при x+ (x - ), если функцию f(x) можно представить в виде f(x) = k x + b + (x), где (x) 0 при x+ (x - ).
Геометрический смысл наклонной асимптоты: Рассмотрим случай x+.
П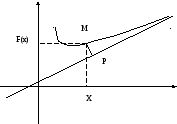
усть
M(x,
y)
– точка
графика функции Y=f(x)
и пусть прямая Y=k
x
+ b
является наклонной асимптотой графика
функции при x+.
Опустим перпендикуляры из точки М
на ось
абсцисс и на асимптоту. Пересечение
первого перпендикуляра с осью ОХ
назовем точкой N(x,
Y1),
а второго – точкой
P.
Тогда
|MN|=|y
- Y1|=|f(x)
– (k
x
+ b)|=|
(x)
| 0
при
x+.
d=|MP|=|MN|
cos
,
где
– угол
между асимптотой и осью ОХ,
и
lim
d=0.
Т. о., расстояние от точки M(x, y) графика функции до асимптоты стремится к 0 при x+, т. е. график функции неограниченно приближается к асимптоте при x+.
ТЕОР1: Для того, чтобы график функции Y=f(x) имел при x+ асимптоту Y=k x + b, необходимо и достаточно существование пределов lim (f(x)/x) =k и lim (f(x) - k x) =b при x+.
Док-во: Необходимость: Пусть график функции Y=f(x) имеет при x+ асимптоту Y=k x + b, т. е. для f(x) справедливо представление f(x) = k x + b + (x). Тогда при x+
lim (f(x)/x) = lim ((k x + b + (x)) /x) = lim (k + b/x + (x)/x) = k и lim (f(x) - k x) = lim (b +(x)) = b.
Достаточность: Пусть существуют пределы lim (f(x)/x) =k и lim (f(x) - k x) =b при x+. Из второго равенства, что разность f(x) - k x - b является бесконечно малой при x+. Обозначим эту бесконечно малую через (x), получим для f(x) представление: f(x) = k x + b + (x).
Для x - аналогично.
-
Понятие первообразной. Теорема и лемма о первообразной.
ОПР1: Функция F(x) называется первообразной для функции f(x) на промежутке X, если для любого x из этого промежутка выполняется условие F’(x)=f(x).
ЛЕММА: Функция, производная которой на промежутке Х равна 0, постоянна на этом промежутке.
Док-во: Пусть для xX f ’(x)=0, тогда для X1, X2X, X1<X2 выполняется формула конечных приращений Лагранжа. (f ’(x)=0 - непрерывна, дифференцирована) f(X2) – f(X1) = f ’()(X2 – X1), ( X1, X2), f ’() =0 f(X1) = f(X2) f(x) = C.
ТЕОР: Если F(x) – первообразная для f(x), на промежутке X, то любая другая первообразная этой функции на промежутке X представлена в виде F(x) +C, где C – произвольная постоянная.
Док-во: Пусть F(x) – первообразная для f(x) на X (xX) F’(x) = f(x). Пусть функция (x) – первообразная для f(x) (xX) ’(x) = f(x). Рассмотрим разность
((x) – F(x))’ = ’(x) – F’(x) = f(x) – f(x) = 0 ((x) – F(x))’ = 0 на X для xX эта функция является постоянной (x) = F(x) + C, где C – произвольная постоянная.