
Линейная зависимость
-
Указать, какие из сформулированных ниже утверждений верны. Система a1, a2, . . ., an линейно зависима тогда и только тогда, когда
(а) существует тривиальная линейная комбинация этой системы, равная нулю;
(б) существует нетривиальная линейная комбинация этой системы, равная нулю;
(в) любая нетривиальная линейная комбинация этой системы равна нулю;
(г) если существует нетривиальная линейная комбинация этой системы, не равная нулю.
-
Указать, какие из сформулированных ниже утверждений верны. Система a1, a2, . . ., an линейно независима, тогда и только тогда, когда
(а) любая линейная комбинация этой системы тривиальна;
(б) любая линейная комбинация этой системы, не равная нулю, тривиальна;
(в) любая линейная комбинация этой системы, равная нулю, тривиальна;
(г) любая нетривиальная линейная комбинация этой системы равна нулю.
-
Известно, что
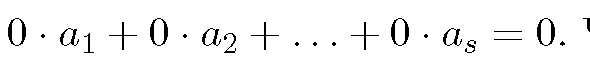 Что
можно сказать о системе a1,
a2,...,
as?
Что
можно сказать о системе a1,
a2,...,
as? -
Даны две системы строк:
![]()
Известно, что первая система линейно независима и каждая ее строка выражается через вторую систему. Тогда
(а) m≥ 15;
(б) m < 15;
(в) m может быть как меньше 15, так и больше 15. Выбрать правильный вариант. Ответ обосновать.
-
Даны три системы строк
![]()
Известно, что первая выражается через вторую, а вторая — через третью.
Тогда первая система строк
(а) линейно зависима;
(б) линейно независима;
(в) может быть как линейно зависимой, так и линейно независимой.
-
Известно, что
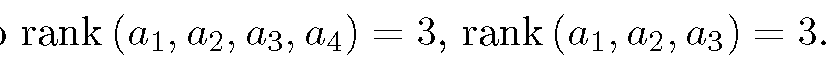 .
Доказать, что a4
выражается через a
, a2,
a
3.
.
Доказать, что a4
выражается через a
, a2,
a
3. -
Построить векторы a , a2, a 3 так, чтобы
(а) rank (a , a2, a 3) = 2, rank (a , a2) = rank (a2, a 3) = 1;
(б) rank (a , a2, a 3) = 2, rank (a , a2) = rank (a2, a 3) = rank (a ,a 3) = 1.
-
Даны четыре строки
![]()
Известно, что строка d не выражается через a, b, с. Тогда система a, b, с
(а) линейно независима;
(б) линейно зависима;
(в) ничего определенного о линейной зависимости этой системы сказать нельзя. Выбрать правильный вариант, ответ обосновать.
-
Дана система строк
![]() Доказать,
что найдется строка d = (s1,s2,s3),
которая не выражается через a,
b,
с.
Доказать,
что найдется строка d = (s1,s2,s3),
которая не выражается через a,
b,
с.
-
Доказать, что если три вектора a, b, с линейно зависимы и вектор с не выражается линейно через векторы a и b, то векторы a и b, различаются между собой лишь числовым множителем.
-
Система векторов a, b, с линейно независима. Доказать, что если вектор b выражается через каждую подсистему этой системы из двух векторов, то b = 0.
-
Дана линейно зависимая система из трех векторов a, b, с ∈ R3. Доказать, что найдется строка d ∈ R3, которая не выражается через систему строк a, b, с.
-
В каком случае система векторов обладает единственным базисом?
-
Привести пример системы из трех строк, который опровергает следующее утверждение: Если некоторая система из n строк линейно зависима, то в ней найдется линейно зависимая подсистема из n - 1 строк.
Перестановки
-
В перестановке (i1, i2,..., in) имеется k инверсий. Сколько инверсий имеется в перестановке (in, in-1,... ,i2, i1)?
-
Сколько инверсий образует число 1, стоящее на k-ом месте перестановки?
-
Сколько инверсий образует число n, стоящее на k-ом месте в перестановке чисел 1, 2, 3,..., n?
-
Чтобы получить одну нечетную перестановку из другой нечетной потребуется не менее двух транспозиций. Доказать.
-
Привести пример таких двух нечетных перестановок, что одну из другой нельзя получить с помощью двух транспозиций. Доказать, что в этом случае для этого требуется не менее четырех транспозиций.
-
Даны две перестановки различной четности. Доказать, что если одну из другой нельзя получить с помощью одной транспозиции, то для получения одной из другой потребуется не менее трех транспозиций.
-
Сколько различных перестановок можно получить из данной перестановки степени n путем применения ровно одной транспозиции. Тот же вопрос для транспозиций соседних элементов.
