Побудова алгоритму

Метод найменших квадратів полягає в наступному Нехай нам задано значення якоїсь функції у=f(x) у вузлах x₀,x₁,...,x_n. Будемо шукати поліном Р(x) степеня меншого за n, який би в точках х_i набував значень у_i не точно, а з деякою похибкою. Нехай

Р(x)=a₀+a₁x+a₂x²+...+a_mx^m , (m<n) (1)

такий, щоб справджувались рівності:

P(x_i)–y_i0, (i=0,1,...,n). (2)

При m=n маємо інтерполювання, що дає змогу використати формулу Лагранжа.

Знаходження коефіцієнтів полінома зводиться до розв’язання системи (2), розв’язати яку без додаткової умови неможливо, бо m<n. Принцип найменших квадратів полягає в тому, що найкращі значення коефіцієнтів поліному (1) ті, при яких сума квадратів відхилень поліному від значень функцій в даних точках найменша. Інакше кажучи, коефіцієнти знаходимо з умови перетворення в мінімум виразу:

(3)

Підставляючи (1) у (3), матимемо поліном другого степеня відносно a_k, (k=0,1,...,m):

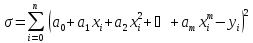(4)

З формули (4) бачимо, що поліном s не може бути менший від нуля, тому поліном існує. Як відомо з математичного аналізу, для знаходження тих значень коефіцієнтів a_k, при яких s перетворюється в мінімум, треба знайти частинні похідні по всіх коефіцієнтах a_k і прирівняти їх до нуля. Дістанемо систему m+1 рівнянь:

(5)

Систему (5) зручно записати в такій формі

, k=0,1,2,...,m.

Звідси одержуємо ітераційні методи побудови вільних членів та коефіцієнтів системи рівнянь:

1. Для поліному степеня m рівняння до першого формується так:

, , , , …,

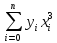2. Кожне рівняння містить невідоме: а_k, а_k–1, а_k–2 ,..., а₁ , а₀ .

3. Послідовність коефіцієнтів при невідомих в першому рівнянні має вид:

, , ,…,

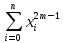4. Щоб одержати послідовність коефіцієнтів при невідомих в j+1-му рівнянні з послідовності коефіцієнтів при невідомих в j-му рівнянні потрібно вилучити перший коефіцієнт, перемістити всі коефіцієнти на одиницю вліво і приєднати справа коефіцієнт рівний сумі х_і з степенями на одиницю меншими ніж їх містить останній коефіцієнт, тобто, якщо ми мали послідовність коефіцієнтів: , , , …, то одержимо послідовність коефіцієнтів: , , …, , .

5. В останньому рівнянні коефіцієнт біля а₀ дорівнює n+1.

Визначник системи (5) не дорівнює нулю, тому вона має розв’язок, що становить сукупність значень коефіцієнтів a_k, які задовольняють умову (3) і перетворюють s в мінімум.

Слід зауважити, що значення s залежить, в значній мірі, від точності обчислення значень функції у(х_і). Якщо у(х_і)=у_і± D_і, то в s присутній доданок (у_і±D_і–р(х_і))²=(у_і–р(х_і))²±2D_і(у_і–р(х_і))+D_і². Отже, похибка D_і при обчисленні значення функції у(х_і) дає додатковий доданок 2½D_і(у_і–р(х_і))½+D_і² при обчисленні s. Тому, досить часто, якщо в якійсь точці відхилення ½у_і–р(х_і)½ значно перевищує відхилення в інших точках, то значенням функції в цій точці ігнорують. Його взагалі відкидають, як помилкове, або обчислюють заново.

Інструкція

Для складання поліномів методом найменших квадратів треба:

1. Користуючись формулою (3), скласти суму s в загальному вигляді.

2. Знайти частинні похідні по всіх a_i і прирівняти їх до нуля. Дістанемо систему рівнянь.

3. Скласти таблицю для обчислення коефіцієнтів знайденої системи.

4. Розв’язати систему і визначити a_k.

5. Скласти поліном і обчислити D_i і s.