ЛАБОРАТОРНЕ ЗАНЯТТЯ №4
«Інтерполяційний поліном Лагранжа»
Постановка задачі
Вважають, що на множині дійсних чисел X визначено деяку дійсну функцію y=f(x), якщо кожному числу x з цієї множини поставлено у відповідність одне дійсне число y з множини Y. На практиці часто трапляються випадки, коли формула задається складним виразом і знайти значення y для відповідних x досить важко. Крім того, часто аналітичний вираз функції y=f(x) взагалі невідомий, а відомі лише її значення в скінченій кількості точок (функція задана таблично). Ці значення можуть бути знайдені в результаті спостережень чи вимірювань в якому-небудь експерименті, або в результаті обчислень. Тому виникає потреба вихідну функцію y=f(x) наближено замінити (апроксимувати) деякою іншою функцією (x), в певному розумінні близькою до f(x) і такою, що простіше обчислюється чи досліджується. Тоді при всіх значеннях аргументу з множини X покладають f(x)(x). Функцію (x) називають апроксимуючою. Близькість функцій f(x) і (x) можна, зокрема, оцінювати в метричних просторах за допомогою відстані. По-різному вводячи відстань, дістають різні конкретні випадки задачі апроксимації.
Часто апроксимуючу функцію (x) беруть у вигляді лінійної комбінації функцій деякого класу, які утворюють скінчену чи зчисленну множину {i(x)}, причому будь-яка скінчена система елементів i(x) лінійно незалежна. Тобто (x) беруть у вигляді
(x) = 00(x) +11(x) + ... + nn(x), (1)
де – 0, 1,...,n сталі коефіцієнти. Функцію (x) в цьому випадку називають узагальненим многочленом. Надалі розглядатимемо наближення функцій узагальненими многочленами.
Нехай у точках x0, x1, ... ,xn (xixj, якщо ij) з відрізка [a,b] відомі значення функції y=f(x): y0=f(x0), y1=f(x1),..., yn=f(xn). Розглянемо один з випадів апроксимації, що називається інтерполюванням, або інтерполяцією. Суть його полягає в тому, що коефіцієнти 0,1,...,n многочлена (1) добирають так, щоб у точках x0,x1,...,xn значення функцій f(x) і (x) збігалися, тобто
,
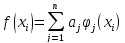i=0,1,...,n.
(2)
Точки x0,x1,...,xn називаються вузлами інтерполювання, а многочлен (x) – інтерполяційним многочленом. Формулу y=(x), знайдену для обчислення значень функції y=f(x), називають інтерполяційною. Задача інтерполювання матиме єдиний розв’язок, якщо при будь-якому розміщенні вузлів визначник системи (2) не дорівнюватиме нулю, тобто
.
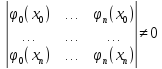Системи функцій, які задовольняють таку умову, називають системами Чебишова. На практиці систему {i(x)} часто беруть у вигляді послідовності цілих невід’ємних степенів змінної x, тобто i(x)=xi (i=0,1,2,...). Тут узагальнені многочлени є звичайними алгебраїчними многочленами. Інтерполювання в цьому випадку називається поліноміальним, або параболічним.
Інтерполяційний поліном Лагранжа
Нехай у точках x0, x1, ... , xn (xixj, якщо ij) з відрізка [a,b] задано значення функції y=f(x): yi=f(xi). Треба побудувати такий поліном Ln(x) = 0+1x+ ... +nxn (степеня, не вищого за n), який у вузлах x0, x1, ... , xn набуває тих самих значень, що й функція y=f(x), тобто
Ln(xi) = f(xi) (i=0, 1, ... , n). (3)
З умови (3) для знаходження коефіцієнтів i (i=0, 1, ... , n) дістаємо систему рівнянь:
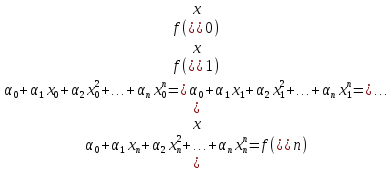(4)
Визначником цієї системи є визначник Ван дер Монда:
,
який,
як відомо, дорівнює
.
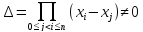Це означає, що функції 1, x,
x2,
..., xn
утворюють систему Чебишева. Отже, система
(4) має єдиний розв’язок при будь-яких
значеннях f(xi)
(i=0,
1,...,n).
Таким чином, коли серед вузлів немає
таких, що збігаються, то алгебраїчний
многочлен існує і єдиний.
Щоб дістати інтерполяційний многочлен у явному вигляді, не станемо розв’язувати систему (4), а побудуємо безпосередньо многочлен Ln(x), який задовольняє умову (3). Многочлен Ln(x) шукатимемо у вигляді лінійної комбінації деяких многочленів степеня n, причому коефіцієнтами цієї лінійної комбінації будуть задані значення функції y=f(x) у вузлах, тобто
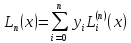(5)
де
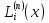(i=0,
1,..., n)
– поки що невідомі многочлени степеня
n.
З умови
(3) випливає, що многочлени
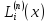мають задовольняти умову
,
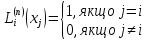тобто
.
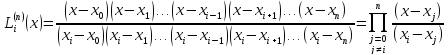Підставивши
вирази
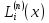у формулу (5), дістанемо вираз інтерполяційного
многочлена Ln(x):
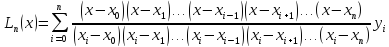(6)
Інтерполяційний
многочлен, записаний у вигляді (6),
називається інтерполяційним многочленом
Лагранжа. Многочлени
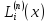називаються коефіцієнтами Лагранжа.
Запишемо формулу Лагранжа для випадку рівновіддалених вузлів. Нехай x1–x0= x2 –x1 = ... =xn–xn–1=h. Для спрощення зробимо заміну x=x0+th. Тоді x–xk=h(t–k) і інтерполяційний поліном Лагранжа матиме вид:
,
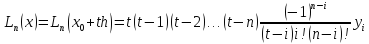де t=(x–x0)/h.