Лекція № 16-17

Тема: Системи звичайних диференціальних

рівнянь.

Задача інтегрування систем звичайних диференціальних рівнянь звучить так: знайти розв’язки системи диференціальних рівнянь:

(1)

Потрібно знайти функції , які перетворюють рівняння системи в тотожності, в області визначення . Зауважимо, що кількість рівнянь завжди рівна кількості шуканих функцій. Якщо ж кількість рівнянь менша кількості шуканих функцій, то система зветься системою рівнянь Монжа. Теорія систем рівнянь Монжа значно складніша від теорії яку ми розглядатимемо в цьому курсі.

Ми будемо розглядати окремі типи рівнянь (системи рівнянь які дозволяють знаходити розв’язки через елементарні функції та інтеграли).

Нехай систему рівнянь (1) можна розв’язати відносно старших похідних:

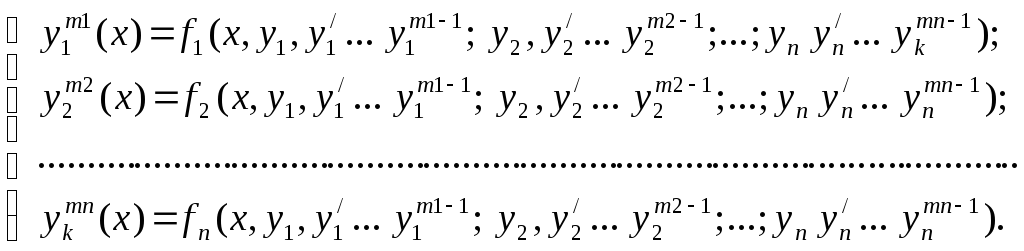(2)

Покажемо, що кожну систему диференціальних рівнянь (2) можна звести до системи диференціальних рівнянь першого порядку, яка містить рівнянь і n невідомих функцій.

Здійснимо позначення:

Тоді маємо:

Отримали сукупність звичайних диференціальних рівнянь першого порядку в яких є кількість невідомих рівнянь і n- невідомих функцій. Запишемо таку ж сукупність для другого рядка:

Об’єднуючи k- сукупностей окремих рівнянь отримаємо систему звичайних диференціальних рівнянь першого порядку, що містить рівнянь і стільки ж невідомих функцій. Якщо невідомі функції пере позначити то система рівнянь (2) перепишеться у вигляді:

(3)

Озн. Система звичайних диференціальних рівнянь записана в формі (2) зветься канонічною системою диференціальних рівнянь (форма Коші).

Озн. Система звичайних диференціальних рівнянь записана в виді (3) зветься системою диференціальних рівнянь.

Твердження 1: Рівняння виду: можна звести до нормальної диференціальної системи рівнянь першого порядку.

Дов: Позначимо:

Тоді:

Отже маємо:

Метод виключення інтегрування нормальної системи диференціальних рівнянь.

Суть методу полягає в тому, що нормальну систему диференціальних рівнянь (3), виключаючи одну за одною невідомі функції, зводять до рівнянь n- ого порядку відносно однієї із невідомих функцій. Знайшовши одну із функцій, знаходять усі інші невідомі функції.

Нехай маємо нормальну систему (3). Диференціюємо перше рівняння по х.

Замінюємо похідні їх виразами з інших рівнянь системи (3). Тоді матимемо рівняння:

Диференціюючи це рівняння і виконуючи ту саму процедуру, що і раніше, знаходимо:

Продовжуючи далі, матимемо:

Отже отримали систему: (4)

З перших n-1 рівнянь цієї системи знайдемо виразивши їх через:

(5)

Зауваження 1: Систему (4) можна розв’язати відносно якщо якобіан відмінний від нуля при розглядуваних значеннях

Підставляючи вирази із (5) в останнє рівняння системи (4) отримаємо рівняння n- ого порядку для визначення : Про інтегрувавши одержимо:

Диференціюючи цю функцію n-1 раз знайдемо похідні як функції від Підставляючи їх у (5), отримаємо невідомі функції:

Зауваження 2: Якщо умова зауваження (2) не виконується то розглянуті випадки не приведуть до рівняння n-ого порядку еквівалентної системи.

Приклад1:

Розв’язати систему диференціальних рівнянь:

Приклад2:

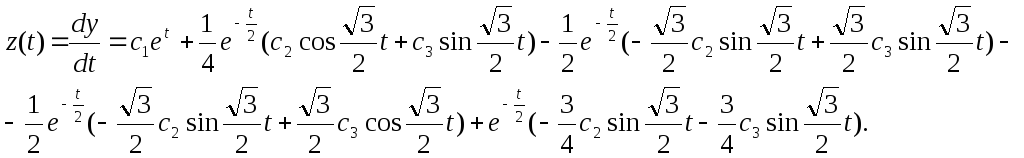
Загальний розв’язок лінійної однорідної системи диференціальних рівнянь із сталими коефіцієнтами.

Якщо в системі (3) функції лінійні відносно невідомих функцій то маємо лінійну нормальну систему диференціальних рівнянь першого порядку виду:

де - задані неперервні функції.

Якщо , то система зветься однорідною.

Якщо хоча б одне , то система зветься неоднорідною.

Нехай задано систему:

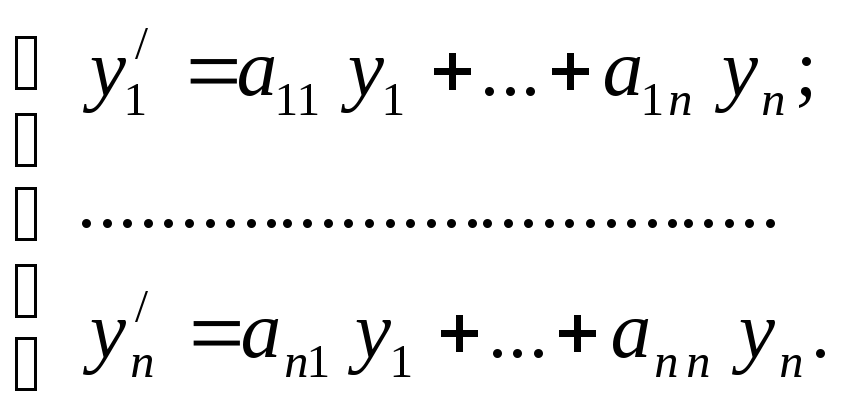(6)

де - сталі величини, .

Розв’язок (нетривіальний) системи шукаємо у вигляді:

.

Підставляючи функції та їх похідні в (6), після скорочення на і перенесення в одну частину рівняння, дістанемо:

(7)

Для того щоб ця система мала розв’язки необхідно і достатньо, щоб її детермінант дорівнював нулю.

Останнє рівняння звуть характеристичним рівнянням. З цього рівняння знаходимо , при яких система (7) має нетривіальні розв’язки . Очевидно, що ліва частина характеристичного рівняння є многочленом степеня n змінної . А такий многочлен має n коренів з врахуванням їх кратності.

Якщо всі n коренів різні, то послідовно для кожного з системи (7) знайдемо відповідний нетривіальний вектор Як відомо, вектори лінійно незалежні, бо всі власні значення різні .

Отже дістанемо n вектор-функцій розв’язків системи (6):

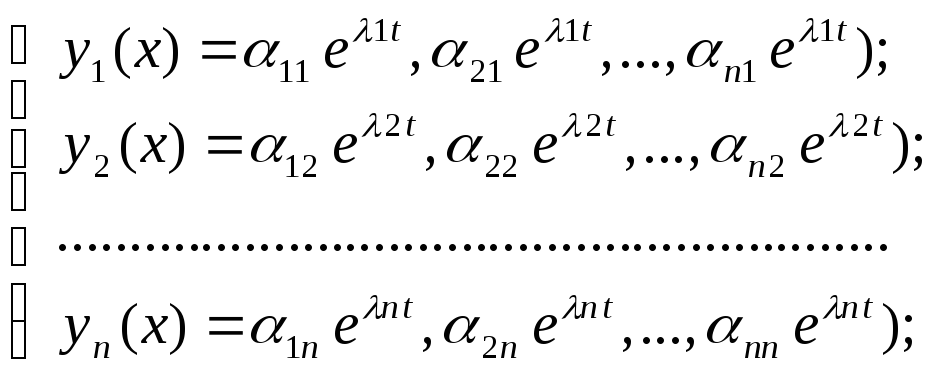
Ці вектор-функції утворюють лінійно незалежну систему на інтервалі бо її детермінант Вронського 0. Тоді загальний розвязок системи (6) при різних коренях характеристичного рівняння має вигляд:

, де - довільні сталі.

Або ще розв’язок можна записати так:

Приклад:

Знайти розв’язок системи лінійних рівнянь.

Тобто

Коренями будуть:

Для кореня складемо систему:

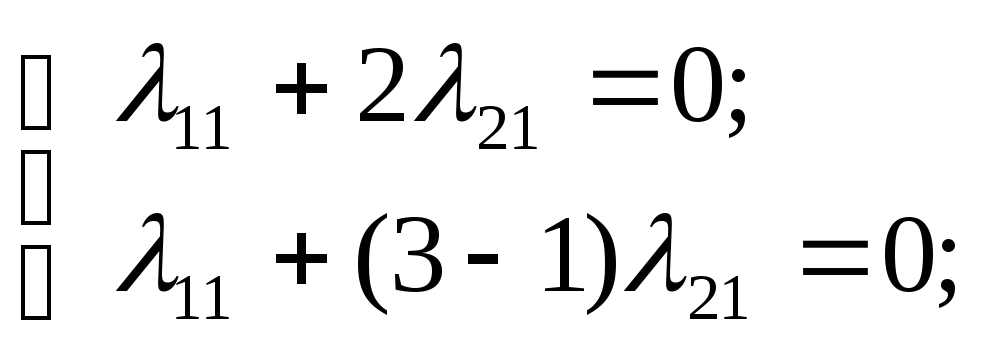
Якщо , то

Для кореня маємо:

Тоді розв’язок буде:

Приклад:

Знайти розв’язок системи: (самостійно).

Якщо корінь характеристичного рівняння системи (6) має кратність r, то переходимо від цієї системи до одного рівняння n-ого порядку відповідно функції

Утворене рівняння і система одне і те ж характеристичне рівняння. Тоді кореню кратності r відповідає розв’язок рівняння n-ого порядку.

, де - довільні сталі. Отже:

, де многочлен степеня r-1. Аналогічно виражаються і інші функції у вигляді .

Зрозуміло, що кожна з функцій задовольняє отриманому диференціальному рівнянню n-ого порядку. З многочленів виберемо такі, щоб відповідні їм функції були розв’язками системи (6). Для цього треба підставити у систему (6), скоротити на і прирівняти коефіцієнти при однакових степенях t.

Знайдені коефіцієнти залежатимуть від r довільних сталих.

Щоб отримати загальний розв’язок системи (6) треба взяти суму вказаних розв’язків (вектор-функції).

Приклад:

Знайти розв’язок системи:

Складемо характеристичне рівняння:

або Тоді: - двократний корінь.

Розв’язок системи треба шукати у вигляді:

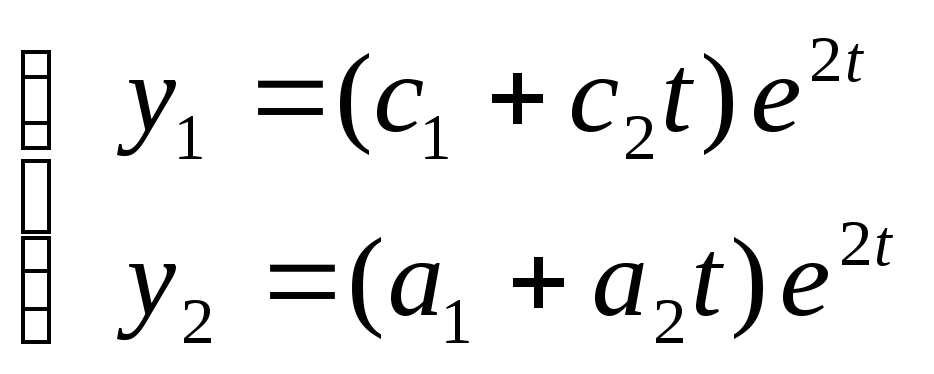
Підставимо ці значення у систему:

Прирівнявши коефіцієнти при однакових степенях t, дістанемо:

Друге рівняння має ті ж розв’язки;

Отже загальним розв’язком системи є: