Лекція № 10-11

Тема: Лінійні диференціальні рівняння n-го порядку.

Озн. Диференціальне рівняння виду:

(1) – наз. звичайним лінійним диференціальним рівнянням n-го порядку. Функції ,

є визначені і неперервні на деякому інтервалі (можуть бути сталими); наз. ще коефіцієнтами рівняння. f(x) – вільний член. Рівняння є лінійним відносно відомої функції ‘y’ і її похідних.

Якщо f(x) = 0, то рівняння звуть однорідним.

(2)

В противному випадку рівняння звуть неоднорідним.

Введемо таке позначення:

L[y] означає, що до функції ‘y’ застосовується усі операції записаного вище лінійного диференціального оператора n-го порядку.

Властивість 1: Якщо та є розв’язками однорідного диференціального рівняння

n-го порядку (2), то їх сума також є розв’язком рівняння (2).

Доведення:

В ході доведення ми показали адитивність оператора L, тобто .

Властивість 2: Якщо є розв’язком рівняння (2), а ‘c’ довільна відмінна від 0, то розв’язком буде .

Доведення:

В ході доведення ми показали однорідність оператора L, тобто

Зауваження:

Якщо - розв’язки рівняння (2), а - довільні сталі відмінні від нуля, то розв’язком рівняння (2) буде: .

В операторно му вигляді матимемо:

.

Очевидно, що у(х) = 0 є розв’язком рівняння (2), і цей розв’язок наз. тривіальним розв’язком.

Тема: Лінійна залежність та незалежність функцій

Введемо поняття лінійної залежності функцій аналогічно до відповідних понять для векторів.

Озн. Систему функцій наз. лінійно-незалежною на АВ, якщо тотожність

(с- const), виконуються тільки тоді, коли всі с= 0. В противному випадку цю систему функцій наз. лінійно-незалежну.

Приклади:

1) . Тоді запишемо:

Система є лінійно-залежною. Фактично, це означає, що ми можемо одну із функцій можемо представити у вигляді лінійної комбінації іншої.

2) Функції - лінійно-незалежні. Переконаємось в цьому. Нехай, ці функції лінійно-залежні, то або або . .

Не зменшуючи загальності вважаємо, що .

Поділимо обидві частини рівняння на .

; Продиференціюємо. Матимемо:

.

Отримали суперечність оскільки жоден із множників 0, а їх добуток рівний.

Озн. Систему з n-лінійно-незалежних на інтервалі АВ розвязків однорідного лінійного диференціального рівняння n-ого порядку наз. фундаментальною системою розв’язків цього рівняння. (щоб розв’язати однорідне рівняння (2) нам потрібно знайти його фундаментальну систему розв’язків.)

Теорема: Якщо функції мають в інтервалі АВ похідні (n -1) – порядку включно і є лінійно-незалежними, то:

Цей визначник (де термінал) позначається: і наз. детермінантом Вронського, або ще наз. Вронськіаном.

Доведення:

Оскільки система функцій лінійно-залежна, то: , причому хоча б одне із сталих ‘с’ відмінне від нуля.

Не зменшуючи загальності, ми завжди можемо поміняти індекс цієї сталої з n. Тоді запишемо ; , .

Про диференціюємо записане рівняння до (n-1) порядку.

……………………………….

Тоді визначник Вронського:

Оскільки останній стовпець визначника є лінійною комбінацією n – 1 - елемента інших стовпців.

Теорема доведена.

Приклад:

Система функцій 1, х, х... х - лінійно незалежна на АВ.

Перевірка: Знайдемо визначник Вронського для цих функцій. Маємо:

Приклад:

Функції e, e… e- лінійно-незалежні якщо k різні числа.

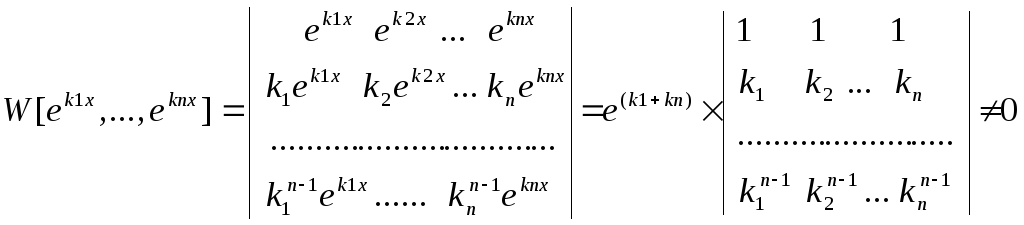
Приклад:

Функції , , , … , - є лінійно незалежні (доведення аналогічно).

Теорема 2:

Для того, щоб розв’язки лінійного однорідного диференціального рівняння (2) були лінійно-незалежні на АВ необхідно і достатньо, щоб детермінант Вронського

W [] 0, .

Доведення:

Якщо визначник Вронського W [] 0, то функції - лінійно-незалежні незалежно від того є вони розв’язками рівняння (2) чи ні (це слідує з теореми (1) ). Нехай ці функції є лінійно-незалежними на інтервалі АВ і є розв’язками рівняння (2). Покажемо, що в цьому випадку визначник Вронського не дорівнює нулю (0 ), для будь-якого x з АВ. Припустимо протилежне: існує точка в якій W [x] = 0, виберемо числа ,

, які є розв’язками системи.

Такі числа ми завжди можемо вибрати оскільки детермінант системи W [x] = 0. Згідно зауваження (1) функція є розв’язком рівняння (2) з нульовими початковими умовами.

Але ці умови задовольняє тривіальний розв’язок у = 0. За теоремою існування та єдиності задачі Коші, рівняння (2) за записаних вище умов має єдиний розв’язок. Тобто:

Звідси випливає (оскільки одночасно), що система функції є лінійно-незалежна. Прийшли до суперечності.

Теорема доведена.

Теорема 3:

Якщо функції є лінійно-незалежними на АВ розв’язками лінійного однорідного диференціального рівняння (2) n-того порядку то функція (x [АВ], - довільні сталі є загальним розв’язком рівняння (2)).

Доведення:

Дійсно які б ми не взяли сталі їх лінійна комбінація : , згідно зауваження (1) буде розв’язком рівняння (2). Нехай також довільним розв’язком цього рівняння буде функція U(x).

Покладемо U(x) = U, U= U, … , U.

Складемо для функцій „U” та чисел U, U, … , U таку систему:

Дана система складена для невідомих . Оскільки є лінійно-незалежні, то визначник Вронського для цієї системи чисел , що задовольняє нашу систему.

Підставимо ці числа в розв’язок рівняння (2), матимемо .

Даний розв’язок задовольняє ті ж самі початкові умови, що і функція U(x), за теоремою існування єдиності розв’язку задачі Коші для рівняння n-ого порядку, звідси слідує, що U(x) = y(x). А це означає, що є загальним розв’язком рівняння (2).

Отже щоб побудувати загальний розв’язок однорідного рівняння (2) потрібно знайти його фундаментальну систему розв’язків та взяти їх лінійну комбінацію, яка і буде загальним розв’язком рівняння (2).

Приклад:

Рівняння має два лінійно-незалежні розв’язки. . Тоді загальний розв’язок запишемо так: .