Лекція №9 Тема: Рівняння вищих порядків. Метод степеневих рядів.

Озн. Звичайне диференціальне рівняння 1-го порядку наз. рівнянням виду:

(1),

В якому функція F вважається неперервною як функція M+2 аргументів в деякій області M+2 вимірного векторного простору. Причому ліва частина рівняння, обов’язково повинна містити M-ту похідну невідомої функції і може не містити саму невідому функцію, аргумент, та всі похідні порядку меншого за М. Якщо зафіксуємо точку:

, що належить області даного рівняння, і припустимо, що в цій точці, та в деякому її околі, функція F є неперервною, та має неперервну похідну (відмінну від нуля), то за відомою теоремою мат. аналізу про неявну функцію в околі цієї точки рівняння (1), може бути розв’язним відносно старшої похідної:

(2).

При певних умовах накладених на функцію F ми можемо говорити, що справедливість теореми існування та єдиності розв’язку задачі Коші:

В рівнянні (2) виконуємо додаткові умови:

Метод степеневих рядів.

Не завжди можна знайти загальний інтеграл рівняння n-ого порядку (1). Часто тоді застосовують наближені методи , зокрема, метод степеневих рядів. Нехай рівняння (1) можна представити у вигляді (2). Відомо, що якщо функція F аналітична в околі початкових значень своїх аргументів , то і розв’язок рівняння y = y(x) є аналітичною в точці . Тому вважаємо, що інтеграл рівняння y = y(x), можна розвинути в ряд Тейлора або Маклорена.

В області збіжності такого ряду дістанемо точний розв’язок y = y(x), рівняння (2). А частинна сума ряду дасть наближений розв’язок.

Суть методу зводиться до того, що нам потрібно знайти коефіцієнти використовуючи рівняння y = y(x) або рівняння (2). Диференціюючи рівняння (2) легко визначають коефіцієнти через перші m з них. Решта коефіцієнтів залишаються невизначеними, і їх можна вважати довільними сталими.

В цьому випадку розв’язок запишемо так:

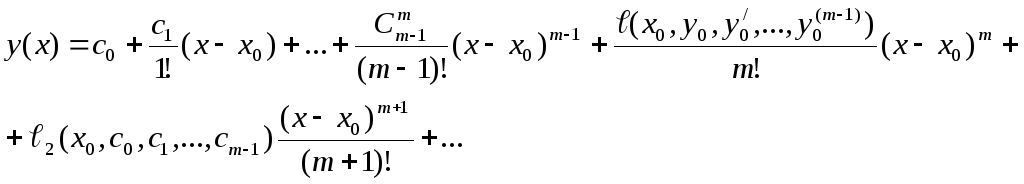
Безпосереднє обчислення коефіцієнтів ряду як правило викликає значні труднощі. Для їх знаходження часто використовують метод невизначених коефіцієнтів. Суть його полягає в тому, що розв’язок шукають у вигляді ряду:

Безпосередньо підставлять цей ряд у диференціальне рівняння і прирівнюють коефіцієнти при однакових степенях x. В результаті дістають систему рівнянь з невідомими ,

, з якої їх і знаходять.

Приклад: Розв’язати рівняння

Попробуємо розв’язок знайти у вигляді ряду Маклорена. Нехай при ;

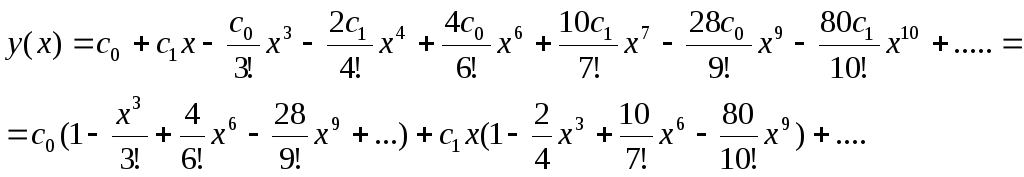
Перевіримо дані ряди на збіжність. Для цього використаємо ознаку Деламбера. Переконавшись, що кожен із рядів є збіжним в околі точки 0, можемо говорити, що отримали степеневий ряд який є розв’язком нашого рівняння.

Приклад: Знайти наближений розв’язок задачі.

Розглянемо частковий випадок рівняння (1) :

()

Тоді про інтегрувавши ліву і праву частину рівняння () попередньо до множивши на dx отримаємо:

Продовживши цей процес будемо мати:

()

Отримали загальний розв’язок рівняння (). Взявши за , а також зробивши пере позначення

Отримаємо:

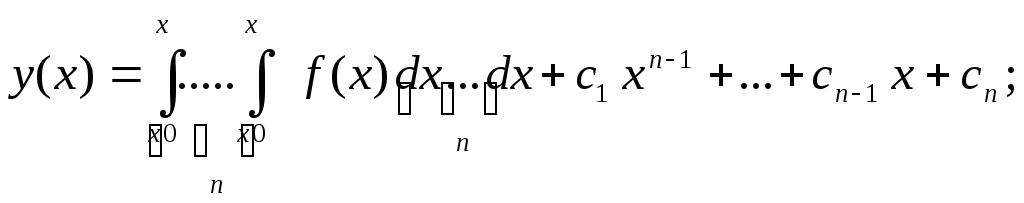
Формула () є розв’язком задачі Коші.

;

Перший доданок формули () є частковим розв’язком рівняння () який перетворюється при в нуль. Перетворимо його (перший доданок) звівши повторний інтеграл, до одного: При n = 2 будемо мати:

(змінимо порядок інтегрування).

;

Використавши метод математичної індукції ми легко доведемо, що для довільного n справджується:

- формула Коші для знаходження розв’язку задачі Коші.

Приклад: Розв’язати рівняння: