Лекція № 13

Тема: Лінійні однорідні рівняння вищого порядку

з сталими коефіцієнтами.

Нехай маємо лінійне однорідне диференціальне рівняння.

(1) , де - сталі. Знайшовши

яку-небудь фундаментальну систему розв’язків ми розв’яжемо це рівняння. Загальним розв’язком буде функція , де - довільні сталі.

Частинні розв’язки шукатимемо у вигляді , k – стала.

Тоді знаходимо похідні до n-го порядку.

Підставимо ці рівності у рівняння (1) здійснивши алгебраїчні перетворення.

Отримаємо: .

Оскільки не може бути рівним нулю, то:

(2)

Отже якщо k – корінь алгебраїчного рівняння (2), то розв’язок рівняння (1), і навпаки. Рівняння (2) звуть характеристичним рівнянням, що відповідає диференціальному рівнянні (1) з сталими коефіцієнтами. Відзначимо, що характеристичне рівняння дістаємо, коли в рівнянні (1) замінимо похідні різних порядків відповідними степенями k. Рівняння (2) має n – коренів з урахуванням кратності кожного з них. А тому різних коренів може бути не більше ніж n – штук.

Випадок простих коренів

Нехай різні корені рівняння (2). Тоді n – функцій є частинними розв’язками рівняння (1). Причому вони є лінійно-незалежними. Загальним розв’язком буде функція: , де - довільні сталі.

Приклад 1:

Розв’язати рівняння: .

Складемо відповідне характеристичне рівняння:

Розв’язавши його отримаємо .

Тоді загальний розв’язок матиме вигляд:

Нехай характеристичне рівняння має комплексний корінь . Тоді ми матимемо такий корінь . З курсу алгебри нам відомо, що якщо алгебраїчне рівняння з дійсними коефіцієнтами має комплексний корінь , то воно обов’язково і має комплексно-спряжений корінь. Матимемо тоді такий розв’язок:

. Використавши формулу Ейлера: .

Тоді наші розв’язки набудуть вигляду:

За теоремою (5) (Л. 10-11) маємо, що комплексному кореню відповідає 2 дійсних розв’язки.

Ці розв’язки є лінійно-незалежними. Комплексно-спряжене також має 2 дійсних корені, вони є ( з точністю до знака ) такими як і для кореня .

Отже парі комплексно-спряжених коренів і відповідає 2 дійсних частинних розв’язки рівняння (1).

Приклад 2:

Розв’язати рівняння:

Складаємо характеристичне рівняння:

Тоді загальний розв’язок матиме вигляд:

Випадок кратних коренів

Припустимо, що характеристичне рівняння має кратні корені. В цьому випадку ми дістанемо менше ніж n частинних розв’язків рівняння (1), а отже ми не можемо знайти фундаментальну систему розв’язків і загальний розв’язок. Потрібно знайти спосіб знаходження всіх частинних розв’язків рівняння (1), які б складали фундаментальну систему розв’язків. Ліву частину характеристичного рівняння (2) позначимо так:

.

Частинні розв’язки рівняння (1) будемо шукати у вигляді: ; де k – корінь характеристичного рівняння, U – невідома функція від х, яку знаходимо так, щоб виконувалась рівність: . Обчислюємо усі похідні функції y(x) до n-того порядку включно. Так використавши формулу Лейбніца:

;

Підставивши знайдені значення похідних у рівняння (1), а також урахувавши вигляд g(k), отримаємо:

(3)

Якщо є коренем характеристичного рівняння кратності 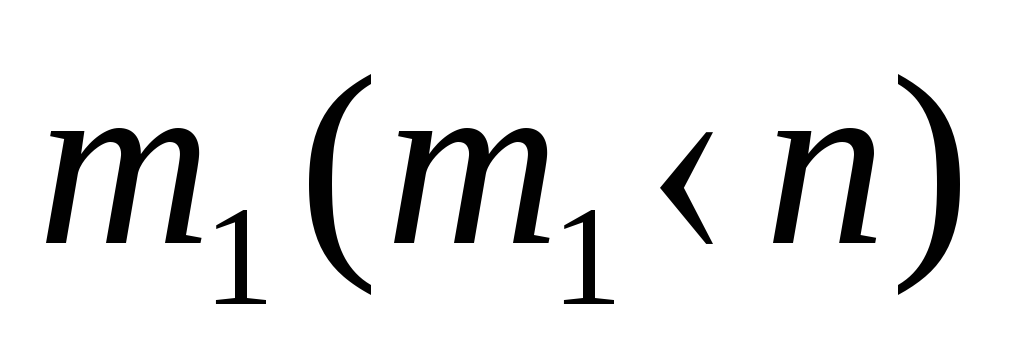, то як відомо з курсу алгебри . То як відомо з курсу алгебри:

. Тоді вираз (3) матиме вигляд:

Тоді функція буде розв’язком рівняння 1, якщо

Оскільки , а також кожен з коефіціентів при , то звідси слідує, що повинно виконуватись: .

Отже логічно за U брати такі функції: 1, х, х, ... , х.

Тоді частинними розв’язками рівняння (1), що відповідають кореню характеристичного рівняння кратності будуть функції: .

Аналогічно кореню кратності будуть відповідати такі частинні розв’язки . Отже в загальному випадку коли характеристичне рівняння має корінь кратності , кратності , ... , кратності , де

. Тоді відповідає система n – різних частинних розв’язків рівняння (1).

Оскільки така система є лінійно-незалежною, то ми маємо фундаментальну систему розв’язків лінійна комбінація яких дає загальний розвяок загальний розв’язок:

Якщо - комплексний корінь кратності m, то спряжене дорівнює теж корінь кратності m. В цій парі коренів відповідатимуть такі частинні розв’язки:

або що те саме ( використавши формулу Ейлера ) матимемо:

.

Тобто комплексному кореню кратності m відповідає 2m частинних розв’язків. Тоді в загальному розв’язку будемо мати:

Приклад 1:

Розв’язати рівняння: .

Складемо відповідне характеристичне рівняння:

Тоді загальний розв’язок буде:

Приклад 2:

Розв’язати рівняння: .

Складемо відповідне характеристичне рівняння:

В цьому випадку ми маємо комплексний корінь 2i. Загальний розв’язок матиме вигляд:

У формулу (3)(Л. 13) замість k підставимо , замість U підставимо Q(x). Позначивши через ліву частину характеристичного рівняння при матимемо:

Скоротивши на отримаємо:

(3)

Якщо не є коренем характеристичного рівняння, тобто , то очевидно, що степінь многочлена повинен збігатися з степенем многочлена .

Припустимо, що ; де - сталі які потрібно знайти. Підставивши многочлен в рівняння (3) та виконавши відповідні алгебраїчні перетворення прирівнявши коефіцієнти при однакових степенях х отримаємо систему

m + 1 рівнянь, розвязавши яку знаходимо невідомі коефіцієнти.

Зауваження:

Оскільки не дорівнює нулю, то система матиме єдиний розв’язок.

Приклад:

Розв’язати рівняння:

Розв’язок даного рівняння шукаємо у вигляді:

;

;

, де А і В – невідомі коефіцієнти. Для того щоб їх знайти підставимо у наше рівняння, попередньо знайшовши відповідні похідні.

;

Прирівнявши коефіцієнти при однакових степенях х отримаємо систему для знаходження невідомих А та В.

;

;

Припустимо, що , тобто - корінь характеристичного рівняння. Нехай цей корінь має кратність . Тоді за відомою теоремою, з курсу алгебри маємо:

.

Тоді рівняння (3) матиме вигляд:

(4)

Степінь многочленів лівої та правої частини рівності (4) повинні бути однаковими, тобто мати степінь m. Це означає, що r – похідна многочлена буде m-го степеня. Що означає, що матиме степінь . Тобто:

(5)

Ліва частина (4) містить похідні з r-тої по m-ту. При підстановці (5)-(4) та знаходженні всіх похідних, члени правої частини (5) починаючи з зникнуть.

Тому доцільно припустити, що коефіцієнти: - рівні нулю. Тоді:

.

Або винісши за дужки отримаємо, що: .

Отже, якщо - корінь характеристичного рівняння кратності r, то частинний розв’язок рівняння (1) шукаємо у вигляді:

, де r - находиться в межах від 0 до n. - многочлен того ж степеня, що і . Отже, щоб знайти коефіцієнти многочлена підставимо в задане рівняння замість “у” вираз . Скорочуємо на , прирівнюємо коефіцієнти при однакових степенях х. Із утвореної системи знаходимо невідомі коефіцієнти .

Приклад 1:

Розв’язати рівняння:

Розв’язок шукаємо у вигляді: ;

Маємо, що - двократний корінь характеристичного рівняння.

Шукаємо відповідні похідні та підставляємо їх значення в рівняння.

;

;

;

;

;

;

Приклад 2:

Розв’язати диференціальне рівняння:

Загальний розв’язок даного рівняння шукаємо у вигляді:

, де - частковий розв’язок рівняння.

, а - розв’язок часткового рівняння: .