2.2.2. Монотонные последовательности

Теорема 5. Всякая ограниченная сверху, монотонно возрастающая последовательность {x_n} имеет конечный предел

Доказательство. Пределом будет число b=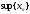. Докажем это. Берем произвольное  >0. Из определения точной верхней грани следует, что найдется N такое, что b- < x_N  b <b+ .

Все последующие члены последовательности будут располагаться в этой -окрестности числа b в силу монотонности последовательности, ч.т.д.

Рис. 2.2

Замечание 1. Аналогично доказывается, что всякая ограниченная снизу монотонно убывающая последовательность сходится.

Замечание 2. Если {[a_n,b_n]} система вложенных стягивающихся к нулю отрезков и с[a_n,b_n], то .

Доказательство:

. Аналогично,

.

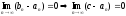Пример. Число e . Число Эйлера или неперово число.

Индукцией по n доказывается формула (Бином Ньютона):

.

Используя формулу бинома Ньютона для последовательности x_n= получим:

+…+…+=

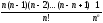Для n+1 будет выполнено, соответственно,

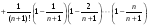
При переходе от n к n+1 каждое слагаемое в этой сумме увеличивается и общее число слагаемых увеличивается на один, поэтому x_n<x_n+1. Далее, каждая скобка <1 и , поэтому

. Монотонно возрастающая ограниченная последовательность сходится к некоторому числу, которое обозначается e.

Это трансцендентное число называется числом Эйлера e=2.718281828459045…

2.3. Некоторые свойства последовательностей, связанные со свойством непрерывности вещественных чисел

Дальнейшие свойства сходящихся и ограниченных последовательностей. Подпоследовательность.

2.3.1.Подпоследовательность. Теорема Больцано-Вейерштрасса

Определение. Дана последовательность {x_n} и последовательность натуральных чисел {n_k}, 1n₁<n₂<…<n_k<n_k+1<…, тогда числовая последовательность {y_k}, называется подпоследовательностью последовательсти {x_n}.

Пример: x_n= sin n, n_k=2k, = sin 2k.

Замечание. Отметим, что из условия n_k < n_k+1 следует, что

k n_k (доказывается индукцией по k) .

Теорема 1. Если (a - число или символ), то для любой ее подпоследовательности {y_k}, ,будет выполнено: .

Доказательство: Вне любой окрестности a содержится лишь конечное число членов {x_n}, следовательно, и конечное число подпоследовательности {}, ч.т.д.

Теорема 2. (Больцано, Вейерштрасс) Из любой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.

Доказательство. Пусть последавательность лежит на

[a,b] {x_n}.

Разделим отрезок [a,b] пополам, обозначим [a₁,b₁] тот из полученных двух отрезков, который содержит бесконечно много членов последовательности {x_n}. Возьмем какой-нибудь член последовательности, лежащий в [a₁,b₁], его индекс обозначим n_1.

Разделим отрезок [a₁,b₁] пополам, обозначим через [a₂,b₂] тот из полученных двух отрезков, который содержит бесконечно много членов последовательности {x_n}. Возьмем какой-нибудь член последовательности, лежащий в [a₂,b₂] и имеющий индекс больший, чем n₁, его индекс обозначим n_2. Продолжая этот процесс, мы построим подпоследовательность 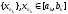. Система отрезков [a_k,b_k] представляет собой систему вложенных, стягивающихся к нулю отрезков (b_k-a_k=(b-a)/2^k). Общую точку обозначим c. Так как c[a_k,b_k], то . Откуда следует, что (Следствие 2 из Теоремы 4 §2).

Определение. Предел подпоследовательности называется частичным пределом (в том числе ). Просто договоримся частичным пределом не считать.

Замечание 1. Частичных пределов у последовательности может быть много.

Пример: Последовательность всех рациональных чисел {r_n} имеет своим частичным пределом любое вещественное число.

Замечание 2. Для того, чтобы a (число или символ) было частичным пределом последовательности {x_n} необходимо и достаточно, чтобы любая окрестность a содержала бесконечно много членов последовательности {x_n}.

Следствие. Если некоторая окрестность a содержит конечное число членов последовательности, то a не является частичным пределом.

Замечание 3. У любой последовательности существует хотя бы один частичный предел (конечный или бесконечный).

Доказательство: Рассмотреть два случая: Ограниченная последовательность. В этом случае утверждение теоремы является следствием теоремы Больцано-Вейерштрасса. В случае неограниченной последовательности для выделения подпоследовательности имеющей пределом  используется определение предела последовательности, имеющей несобственный предел. Например, пусть , тогда. Условие n_k> n_k-1 можно обеспечить, используя то, что в любой окрестности + имеется бесконечно много членов последовательности.