3.5.7.Непрерывность элементарных функций

1) Непрерывность функции a^x, a>0.

Справедливо равенство .

a) Если a>1, обозначим , a=(_n+1)ⁿ > n_n, _n<a/n , следовательно _n – б.м..

Замечание. Отметим, что точно также можно доказать равенство . Именно, 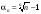, n=(_n+1)ⁿ > ,

_n< , следовательно _n – б.м..

b) Если a <1,то , b > 1.

Докажем, что (непрерывность в 0 функции a^x ).

1 a> 1.

Докажем вначале, что 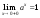. Пусть {x_k} последовательность типа Гейне для , то есть, x_k0, x_k>0. Можно считать, что . Для последовательности целых частей 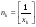будут выполнены неравенства . Откуда, в частности, следует, что n_k+ и далее, переходя к пределу при k , получим требуемое равенство (определение одностороннего предела по Гейне). Аналогично рассматривается случай x 0 - 0. Из существования и равенства односторонних пределов следует доказываемое утверждение: .

2 Если a<1, то b^x=1/a^x,где b=1/a > 1.

2) Функция a^x непрерывна в точке x_{0 .} Это следует из равенства .

3). Функция y=log_ax непрерывна, как обратная к непрерывной строго монотонной функции x=a^y .

4). Степенная функция y=x^. Докажем непрерывность при x>0. Имеем x^=e^{ ln x}, далее следует воспользоваться теоремой о непрерывности суперпозиции. Если допускает отрицательные значения для функции y=x^ , то для доказательства непрерывности этой функции при функцию можно представить в виде: . Непрерывность в нуле рекомендуется попробовать доказать самостоятельно (непосредственно по определению).

5). . Другими словами, или

Доказательство. Функция 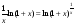непрерывна, как суперпозиция непрерывной и имеющей предел функции: 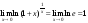. Аналогично доказывается, что

6) 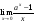= ln a . Другими словами, или .

Доказательство. Обозначим a^x - 1=y, тогда x ln a=ln(1+y),

Стремление к нулю x 0 эквивалентно стремлению к нулю y 0,

.

Пример 1 (Следствие из предыдущего примера). Таким образом, или .

Пример 2. Вычислить предел .

.

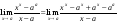Отдельно вычислим пределы и

===

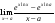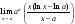=====a^a ,

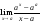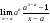==a^aln a .

=a^a(ln a + 1).

7) . Таким образом,  или .

Доказательство. Обозначим (1+x)^ - 1=y, тогда  ln(1+x) = ln(1+y).

.

Пример 3. Вычислить предел .

.

Отдельно вычислим пределы и

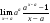==a^a ln a,

=-= =

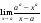==-a^a.

= a^a(ln a - 1).

8) Вычислить предел .

тогда

Поэтому .

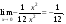
9) Непрерывность .

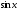|sin x –sin x₀|=2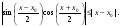

Непрерывность cos x следует из свойств непрерывных функция: cos x = sin(x+/2).

Непрерывность тригонометрических функция tg x, ctg x, arcsin, arcos, arctg, arcctg в своих областях определения следует из свойств непрерывных функций. Например, tg x непрерывен для всех кроме точек, в которых имеется разрыв второго рода.

10) f=const, многочлен P_n(x)=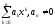является непрерывными функциями всюду, рациональная функция

непрерывна всюду, кроме нулей знаменателя.

3.5.8.Равномерная непрерывность

Функция f(x), определенная на Х называется равномерно непрерывной на Х, если

x,xX,|x-x|<: |f(x)-f(x)|<.

Непосредственно из определения следует, что всякая равномерно непрерывная функция на Х непрерывна в любой точке этого множества. Здесь предполагается выполненным предусловие непрерывности. Именно, если 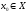, то определена хотя бы в проколотой окрестности точки , быть может, односторонней. Обратное, вообще говоря, неверно. То есть, непрерывная на функция не обязана быть равномерно непрерывной на этом множестве. Примером может служить функция 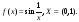Однако, справедлива теорема

Теорема ( Кантор). Всякая непрерывная на [a,b] функция f равномерно непрерывна на [a,b].

Доказательство. От противного.

₀>0>0 u,v [a,b],|u-v|<:|f(u) - f(u)|₀. Для =1/n  u_n,v_n,| u_n-v_n|<1/n:

|f(u_n) - f(v_n)|₀. (1)

По теореме Больцано-Вейрштрасса  = x₀[a,b], тогда и 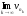= x₀. В силу непрерывности функции,

. Таким образом,

, что противоречит (1).

Приведем достаточное условие отсутствия равномерной непрерывности функции.

Теорема. Пусть функция непрерывна на и существуют две последовательности из области , сходящиеся к некоторому общему значения и такие, что . Тогда функция не является равномерно непрерывной на .

Доказательство. Для определенности будем считать, что . Выпишем отрицание равномерной непрерывности:

₀>0>0 u,v X,|u-v|<:|f(u) - f(u)|₀ (2)

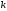Возьмем и для произвольного выберем так, чтобы

а) и

б)

Выполнение первого условия для достаточно больших k следует из равенства пределов . Что касается второго условия, то оно может быть получено из условия из которого и следует выполнение условия б) для достаточно больших номеров. Таким образом, утверждение (2) доказано.

Пример. Воспользуемся доказанной теоремой, чтобы доказать, что функция не является равномерно непрерывной на . В качестве требуемых последовательностей выберем последовательности: , то есть, , а выберем так, что , то есть Указанные последовательности удовлетворяют условиям теоремы и требуемое утверждение доказано.