3.5.2.Простейшие свойства непрерывных функций

1) Сумма, разность и произведение двух непрерывных функций в точке является непрерывной функцией в этой точке.

Следствие: Сумма, разность и произведение двух непрерывных функций на множестве является непрерывной функцией на этом множестве.

2) Сохранение знака непрерывной функции:

f(x₀)>0U(x₀):.

3) Если f(x) непрерывна в точке x₀, g(x) непрерывна в x₀, g(x₀)0, то функция непрерывна в x₀.

4) Функция |f(x)| непрерывна, если непрерывна f(x).

5) Суперпозиция непрерывных функций есть непрерывная функция.

Если f(x) определена в окрестности x₀ и непрерывна в x₀,

g(x) определена в окрестности t₀ и непрерывна в t₀, g(t₀)=x₀. Тогда в некоторой окрестности тоски t₀ определена суперпозиция F(t)=f(g(t)) и F(t) непрерывна в t_0.

Все перечисленные свойства являются непосредственным следствием соответствующих свойств пределов функций.

Классификация точек разрыва

Если f(x) не является непрерывной в точке x₀ , то x₀ – точка разрыва. В этом случае говорят, что функция разрывная (разрывна) в точке x₀ , или , функция претерпевает разрыв в точке x₀ .

Определение. Если существуют конечные пределы

f(x₀ - 0)f(x) и f(x₀+0)f(x)

и f(x) разрывна в точке x₀ , то такой разрыв называется разрывом первого рода. Если при этом , то разрыв называется устранимым.

Разрыв не первого рода называется разрывом второго рода.

Различают конечные и бесконечные разрывы второго рода.

Аналогично классифицируются разрывы для функции, определенной в полуокрестности точки. Например, пусть функция f(x) определена на отрезке [a,b]. Если существует конечный предел f(a+0) и , то разрыв называется разрывом первого рода

Пример 1. Функция имеет устранимый разрыв первого рода в точке .

Рис. 3.4

График функции

Пример 2. Функция имеет разрыв второго рода в точке

Рис. 3.5

Пример 3. Функция = sign x имеет не устранимый разрыв первого рода в точке

Пример 4. Функция = sign x имеет устранимый разрыв первого рода в точке справа.

Пример 5. Функция = sign x имеет устранимый разрыв первого рода в точке слева.

Рис. 3.6

3.5.3. Ограниченность непрерывной функции. Теоремы Вейерштрасса

Лемма. Если {x_n}[a,b] и x_n=x₀, то x₀[a.b].

Доказательство. Теорема о переходе к пределу в неравенствах: .

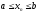Теорема 1 (Первая теорема Вейерштрасса). Непрерывная на [a,b] функция f ограничена на [a,b].

Доказательство (От противного). Ограниченность: Mx[a,b]:|f(x)|M. Отрицание Mx[a,b]:|f(x)|>M. В частности, n x_n[a,b]:|f(x_n)|>n. По теореме Больцано-Вейерштрасса найдется сходящаяся подпоследовательность {} x₀, x₀[a,b]. Тогда, с одной стороны |f()|>n_k, с другой стороны f()f(x₀).

Теорема 2. Непрерывная на [a,b] функция f(x) достигает своих точных верхней и точной нижней граней.

Доказательство. Пусть M= f(x), тогда, беря в качестве . Выберем сходящуюся подпоследовательность x₀, x₀[a,b], . Переходя к пределу в этих неравенствах при k получим требуемое равенство f(x₀)=M.

Рис. 3.7

3.5.4.Теорема о промежуточных значениях непрерывной функции

Теорема. Если непрерывная на [a,b] функция f(x) принимает на концах промежутка [a,b] значения разных знаков, то c(a,b): f(c)=0.

Доказательство. Пусть, например, A=f(a)< 0, B=f(b)> 0. Далее производится последовательное деление отрезка пополам так, что f(a_n)< 0< f(b_n). Общий шаг этого процесса. Дано: f(a_n)< 0< f(b_n). Обозначим середину отрезка [a_n, b_n] через c_n=.

Рис. 3.8

Если , то нужная точка найдена.

Если , то полагаем .

Если , то полагаем .

Этот процесс может оборваться на некотором шаге и, таким образом, нужная точка c будет найдена. В противном случае в результате этой процедуры будет построена последовательность вложенных, стягивающихся к нулю отрезков {[a_n, b_n]} , таких, что f(a_n)<0< f(b_n). Пусть c – общая точка для этих отрезков: a_n c b_n.

Тогда из условия b_n - a_n 0 следует, что 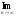a_n=c=b_n , далее из условия f(a_n)< 0< f(b_n) получим, что f(c) 0 f(c).

Следствие 1. Если f непрерывна на [a,b], f(a)f(b). Тогда для M из промежутка f(a), f(b) c[a,b]:f(c)=M.

Доказательство: Пусть, например, A=f(a)<B=f(b), доказанную теорему применяем к функции F(x)=f(x) – M .

Рис. 3.9

Следствие 2. Пусть f(x) непрерывна на отрезке X и , тогда множеством значений этой функции будет отрезок [m,M].

Действительно, по второй теореме Вейерштрасса точные верхние грани достигаются. Таким образом, существуют такие, что и . К точкам применяем следствие 1.

Рис. 3.10