9. Экстремум функции двух переменных

Понятия max, min, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной переменной. Пусть функция Z= f(x; у) определена в некоторой области D и т. М принадлежит к этой области. Точка М называется точкой max функции Z= f(x; у), если существует такая δ-окрестность точки , что для каждой точки из этой окрестности выполняется неравенство . Аналогичным образом определяется и точка min, только знак неравенства при этом изменится . Значение функции в точке max (min) называется максимумом (минимумом). Максимум и минимум функции называются экстремумами.

9. Необходимые и достаточные условия экстремума

Теорема: (Необходимые условия экстремума). Если в точке М дифференцируемая функция Z= f(x; у) имеет экстремум, то ее частные производные в этой точке равны нулю: ,.

Доказательство: зафиксировав одну из переменных x или y, превратим Z= f(x; у) в функцию одной переменной, для экстремума которой вышеописанные условия должны выполняться. Геометрически равенства и означают, что в точке экстремума функции Z= f(x; у), касательная плоскость к поверхности, изображающую функцию f(x,y)=Z параллельна плоскости OXY, т.к. уравнение касательной плоскости есть Z=Z_0. Точка, в которой частные производные первого порядка функции Z= f(x; у) равны нулю, т.е. ,, называются стационарной точкой функции. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например Z=|-| имеет max в точке O(0,0), но не имеет в этой точке производных.

Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Например, при Z=xy точка O(0,0) является критической. Однако экстремума в ней функция Z=xy не имеет. (Т.к. в I и III четвертях Z>0, а в II и IV – Z<0). Таким образом для нахождения экстремумов функции в данной области необходимо подвергнуть каждую критическую точку функции дополнительному исследованию.

Теорема: (Достаточное условие экстремумов). Пусть в стационарной точке и некоторой окрестности функция f(x; у) имеет непрерывные частные производные до 2^ого порядка включительно. Вычислим в точке значения , и . Обозначим

Тогда:

1. если , то f(x; у) в точке 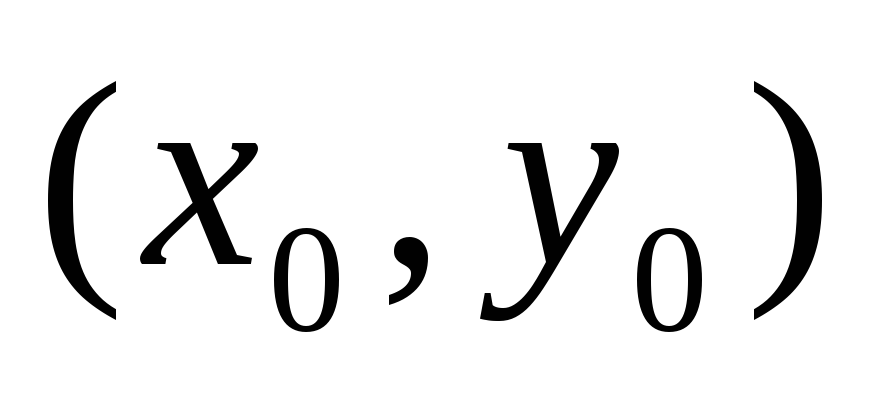имеет экстремум max, если А<0 и min, если А>0.

2. если , то f(x; у) в точке экстремума не имеет.

В случае если , экстремум в точке может быть, а может и не быть. Необходимы дополнительные исследования.

II. Неопределенный интеграл

1. Понятие неопределенного интеграла

В дифференцируемом исчислении мы решали задачу как по данной функции f(x) найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную (или дифференциал). Искомую функцию F(x) называют первообразной функции f(x).

F(x) – называется первообразной функции f(x) на интервале (a, b), если для любого выполняется равенство (или.

Например, первообразной функции является функция , так как .

Очевидно, что первообразными будут также любые функции , где С – постоянная, поскольку .

Теорема 1. Если F(x) является первообразной функции f(x) на , то множество всех первообразных для f(x) задается формулой , где С – постоянное число.

Док-во. Функция - первообразная f(x). Действительно, . Пусть некоторая другая отличная от первообразная функции , т.е. =. Тогда для любого имеем , а это означает, что , где С - . Следовательно, .

Множество всех первообразных функций для называется неопределенным интегралом от функции и обозначается символом . Таким образом =.

Здесь - называется подынтегральной функцией, - подынтегральным выражением, x – переменной интегрирования, - знаком неопределенного интеграла. Операция нахождения неопределенного интеграла – интегрированием этой функции.