
- •Часть II
- •I.Функции нескольких переменных
- •Функция двух переменных
- •Предел функции
- •Непрерывность функции двух переменных
- •Производные и дифференциалы функции нескольких переменных
- •Частные производные высших порядков
- •Дифференцируемость и полный дифференциал функции
- •Дифференциалы высших порядков
- •Производная сложной функции. Полная производная
- •8.Инвариантность формы полного дифференциала
- •Дифференцирование неявной функции
- •Производная по направлению
- •Градиент
- •Экстремум функции двух переменных
- •Необходимые и достаточные условия экстремума
- •II. Неопределенный интеграл
- •Понятие неопределенного интеграла
- •2. Свойства неопределенного интеграла
- •3. Таблица основных неопределенных интегралов
- •4. Основные методы интегрирования
- •5. Интегрирование рациональных функций.
- •6. Интегрирование тригонометрических функций
- •7. Интегрирование иррациональных функций
- •III. Определенный интеграл
- •Определение определенного интеграла
- •Геометрический смысл определенного интеграла
- •3) Работа переменной силы
- •Формулы Ньютона-Лейбница
- •Основные свойства определенного интеграла
- •Вычисление определенного интеграла
- •Несобственные интегралы
- •7. Применение определенных интегралов для расчета геометрических и физических величин различного рода
- •7.1. Вычисление площадей плоских фигур
- •7.2 Вычисление длины дуги плоской кривой
- •7.3 Вычисление объема тела
- •8. Приближенное вычисление определенного интеграла
- •8.1. Формулы прямоугольников
- •8.2. Формула трапеций
- •8.3. Формула парабол (Симпсона)
- •IV. Кратные интегралы
- •4.1. Двойной интеграл. Основные понятия
- •4.2. Геометрический смысл двойного интеграла
- •4.3. Основные свойства двойного интеграла
- •4.4.Вычисление двойного интеграла
- •4.5. Приложения двойного интеграла
- •Статические моменты и центр тяжести плоской фигуры
- •4.6. Тройной интеграл. Основные понятия
- •4.7. Вычисление тройного интеграла.
- •4.8. Приложения тройного интеграла
- •V. Числовые ряды
- •5.1. Основные понятия
- •5.2. Необходимый признак сходимости числового ряда
- •5.3. Достаточные признаки сходимости знакопостоянных рядов
- •5.4. Признак Даламбера
- •5.5. Радикальный признак Коши
- •5.6. Интегральный признак Коши. Обобщенный гармонический ряд
- •5.7. Знакочередующиеся и знакопеременные ряды Признак Лейбница
- •5.8. Абсолютная и условная сходимость числовых рядов
- •VI.Степенные ряды
- •1 Функциональные ряды
- •1.1 Основные понятия
- •2. Некоторые приложения степенных рядов
- •2.1. Приближенное вычисление значений функций
- •2.2. Приближенное вычисление определенных интегралов
- •VII. Ряды Фурье
- •7.1. Основные понятия
- •7.2. Тригонометрический ряд Фурье
- •7.3 Разложение в ряд Фурье 2π-периодических функций. Теорема Дирихле
- •7.4. Разложение в ряд Фурье четных и нечетных функций
- •7.5. Разложение в ряд Фурье функций произвольного периода
- •VIII. Дифференциальные уравнения (д.У.)
- •8.1. Общие сведения на основании понятия о д.У.
- •8.2. Дифференциальное уравнение первого порядка
- •3. Линейные уравнения
- •Метод Бернулли
- •8.3.Дифференциальные уравнения высших порядков
- •1.Решение путем понижения порядка уравнения.
- •2.Линейные дифференциальные уравнения высших порядков.
- •8.4. Решение ду второго порядка с постоянными коэффициентами.
- •1.Решение лоду второго порядка с постоянными коэффициентами.
- •2. Решение лоду n –го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения (лнду)
- •1.Структура общего решения лнду второго порядка.
- •2.Метод вариации произвольных постоянных.
- •3.Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.
- •4.Решение лнду n- го порядка с постоянными коэффициентами и правой специальной частью.
- •Системы дифференциальных уравнений
- •Решение нормальных систем.
- •2.Системы линейных ду с постоянными коэффициентами.
-
Линейные неоднородные дифференциальные уравнения (лнду)
1.Структура общего решения лнду второго порядка.
Рассмотрим ЛНДУ второго порядка
![]() (20)
(20)
Где
![]()
![]() - заданные непрерывные на (a,b)
функции ,уравнение
- заданные непрерывные на (a,b)
функции ,уравнение
![]() левая часть которого совпадает с левой
частью нашего уравнения называется
соответствующим ему однородным
уравнением .
левая часть которого совпадает с левой
частью нашего уравнения называется
соответствующим ему однородным
уравнением .
Теорема : Общим решением
уравнения (20) (y) является
сумма его произвольного частного решения
y* и общего решения
![]() соответствующего однородного уравнения
т.е.
соответствующего однородного уравнения
т.е.![]() .
Доказательство этой теоремы опустим.
.
Доказательство этой теоремы опустим.
2.Метод вариации произвольных постоянных.
Рассмотрим ЛНДУ (20) .Его общим решением,
согласно только, что приведенной теоремы
является соотношение
![]() .
Чаcтное решение y*
уравнения (20) можно найти ,если известно
общее решение
.
Чаcтное решение y*
уравнения (20) можно найти ,если известно
общее решение
![]() соответствующего
однородного уравнения
соответствующего
однородного уравнения
![]() ,
методом вариации произвольных постоянных
(метод Лагранжа), состоящий в следующем.
Пусть
,
методом вариации произвольных постоянных
(метод Лагранжа), состоящий в следующем.
Пусть
![]() - общее решение однородного уравнения.
- общее решение однородного уравнения.![]() Заменим
в общем решении постоянные
Заменим
в общем решении постоянные
![]() и
и
![]() неизвестными
функциями
неизвестными
функциями
![]() и
и
![]() и
подберем их так, чтобы функция
и
подберем их так, чтобы функция
![]() была
решением уравнения (20).Найдем производную
была
решением уравнения (20).Найдем производную
![]()
Подберем функции
![]() и
и
![]() так, чтобы
так, чтобы
![]() ,
(21), тогда
,
(21), тогда
 , а
, а
![]() .
.
Подставляя выражения для y*
,![]() и
и
![]() в уравнение (20) получим
в уравнение (20) получим
 или…
или…
Поскольку
![]() и
и
![]() - решение соответствующего однородного
уравнения, то выражения в квадратных
скобках равны нулю, и поэтому
- решение соответствующего однородного
уравнения, то выражения в квадратных
скобках равны нулю, и поэтому
![]()
![]() (22)
(22)
Таким образом, функция y*
будет частным решением уравнения (20)
если
![]() и
и
![]()
удовлетворяют системе уравнений (21) и (22).
 (23)
(23)
Определитель системы
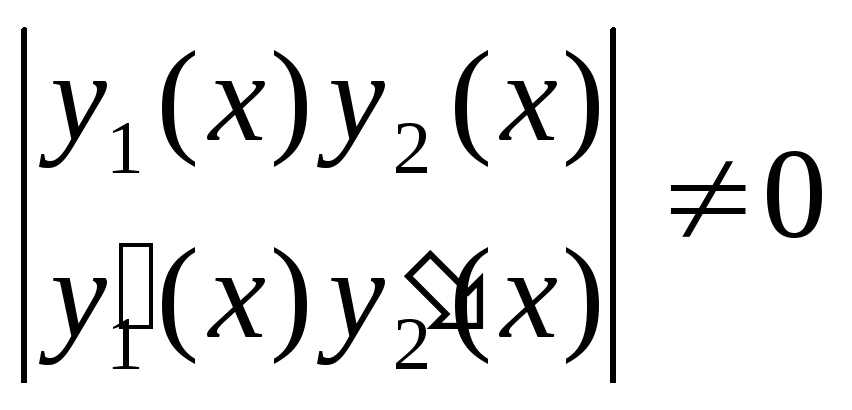 ,так как это определитель для фундаментальной
системы частных решений
,так как это определитель для фундаментальной
системы частных решений
![]() и
и
![]() однородного уравнения .Поэтому система
(23) должна иметь единственное решение
однородного уравнения .Поэтому система
(23) должна иметь единственное решение
![]() и
и
![]() ,
где
,
где
![]() и
и
![]() -
некоторые функции от x.
Интегрируя эти функции находим
-
некоторые функции от x.
Интегрируя эти функции находим
![]() и
и
![]() ,
а затем , в соответствии с формулой для
у* составляем частное решение уравнения
(20).
,
а затем , в соответствии с формулой для
у* составляем частное решение уравнения
(20).
Пример :
![]() ;
;
Найдем общее решение
![]() соответствующего однородного уравнения
соответствующего однородного уравнения
![]() .
Имеем
.
Имеем

![]()
Следовательно,
![]() .Теперь
найдем частное решение у* исходного
уравнения .Оно, как говорилось выше,
ищется в виде
.Теперь
найдем частное решение у* исходного
уравнения .Оно, как говорилось выше,
ищется в виде
![]() .Для
нахождения
.Для
нахождения
![]() и
и
![]() составим
систему уравнений
составим
систему уравнений

Решаем ее

 ;
;

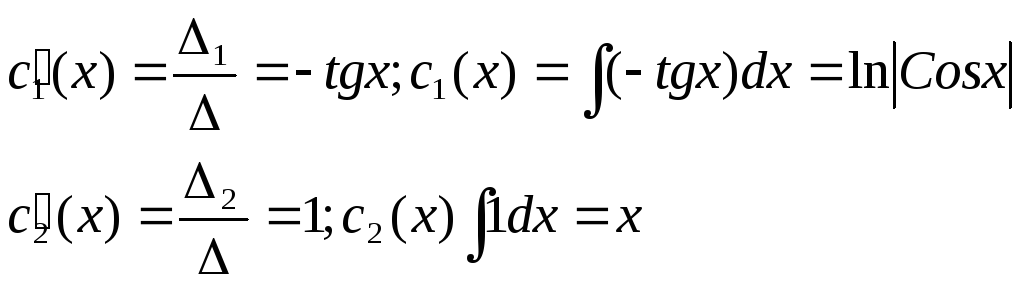
Запишем частное решение данного уравнения
![]() .Следовательно,
общее решение данного уравнения имеет
вид
.Следовательно,
общее решение данного уравнения имеет
вид
![]() .
.
При нахождении частных решений ЛНДУ может оказаться полезной следующая теорема:
Теорема: Если правая часть
уравнения (20) представляет собой сумму
двух функций
![]() ,
а
,
а
![]() и
и
![]() -
частные решения уравнений
-
частные решения уравнений
![]() и
и
![]() соответственно, то функция
соответственно, то функция
![]() является частным решением данного
уравнения.
является частным решением данного
уравнения.
3.Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.
Рассмотрим ЛНДУ второго порядка с постоянными коэффициентами т.е. уравнение
![]() (24)
(24)
Где p и g –
некоторые числа согласно вышеприведенной
теореме.
![]() Общее
решение этого уравнения представляет
собой сумму общего решения
Общее
решение этого уравнения представляет
собой сумму общего решения
![]() соответствующего
однородного уравнения и частного решения
у* неоднородного. Частное решение может
быть найдено методом вариации произвольных
постоянных.
соответствующего
однородного уравнения и частного решения
у* неоднородного. Частное решение может
быть найдено методом вариации произвольных
постоянных.
Однако, для уравнений с постоянными
коэффициентами существует более простой
способ нахождения у* ,если правая часть
![]() уравнения имеет «специальный вид»:
уравнения имеет «специальный вид»:![]()
I .
![]() или II.
или II.
![]()
Cуть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части f(x) уравнения (24) записывают ожидаемую форму частного решения с неопределенными коэффициентами , затем подставляют его в уравнение (24) и из полученного тождества находят значение коэффициентов.
Вариант 1. Правая часть имеет вид
![]() ,
где
,
где
![]() -
многочлен степени n.
-
многочлен степени n.
Уравнение (24) запишется в виде
![]() (25)
(25)
В этом случае частное решение y*
ищется в виде
![]() .
Здесь r – число равное
кратности
.
Здесь r – число равное
кратности
![]() ,
как корня характеристического уравнения.
,
как корня характеристического уравнения.
![]() (т.е. r – число, показывающее,
сколько раз
(т.е. r – число, показывающее,
сколько раз
![]() является корнем уравнения
является корнем уравнения
![]() ),
а
),
а
![]() - многочлен степени n ,
записанный с неопределенными коэффициентами
- многочлен степени n ,
записанный с неопределенными коэффициентами
![]()
а) Пусть
![]() не является корнем характеристического
уравнения
не является корнем характеристического
уравнения
![]() т.е.
т.е.
![]() .
Следовательно,
.
Следовательно,
![]()
После подстановки функции y*
и ее производных в уравнение (25) и
сокращения на
![]() ,
получим :
,
получим :![]() (26)
(26)
Слева многочлен степени n
с неопределенными коэффициентами,
справа – многочлен степени n
, но с известными коэффициентами.
Приравнивая коэффициенты при одинаковых
степенях, получим систему (n
+ 1) алгебраических уравнений для
определения коэффициентов
![]() .
.
б) Пусть
![]() является однократным (простым) корнем
характеристического уравнения
является однократным (простым) корнем
характеристического уравнения
![]() ,т.е.
,т.е.
![]() .
В этом случае искать решение в форме
.
В этом случае искать решение в форме
![]() нельзя
, т.к.
нельзя
, т.к.
![]() ,
и уравнение (26)принимает вид
,
и уравнение (26)принимает вид
![]() .
.
В левой части многочлен степени (n-1) , а в правой многочлен степени n .Чтобы получить тождество многочленов в решении у* нужно иметь многочлен тоже степени
(n-1), поэтому частное
решение у* следует искать в виде
![]() (в
частном решении положить (r
= 1)).
(в
частном решении положить (r
= 1)).
в) Пусть
![]() является двукратным корнем
характеристического уравнения
является двукратным корнем
характеристического уравнения
![]() ,
т.е.
,
т.е.
![]() .
В этом случае
.
В этом случае
![]() ,
а поэтому уравнение (26) принимает вид
,
а поэтому уравнение (26) принимает вид
![]() .
Слева стоит многочлен степени n-2.
Понятно, что чтобы иметь слева многочлен
степени n ,частное решение
у* следует искать в виде
.
Слева стоит многочлен степени n-2.
Понятно, что чтобы иметь слева многочлен
степени n ,частное решение
у* следует искать в виде
![]() ( т.е. в частном решении уравнения надо
положить r =2).
( т.е. в частном решении уравнения надо
положить r =2).
Вариант 2. Правая часть уравнения (24) имеет вид
![]() , где
, где
![]() -
многочлены степени n и m
соответственно,
-
многочлены степени n и m
соответственно,
![]() -
действительные числа. Уравнение (24)
запишется в виде
-
действительные числа. Уравнение (24)
запишется в виде
![]() (27)
(27)
Можно показать, что в этом случае частное решение у* последнего уравнения следует искать в виде
![]() (28)
, где
(28)
, где
r – число , равное кратности
![]() , как корня характеристического уравнения
, как корня характеристического уравнения
![]() ,
,
![]() -
многочлены степени
-
многочлены степени
![]() с
неопределенными коэффициентами,
с
неопределенными коэффициентами,
![]() -
наивысшая степень многочленов
-
наивысшая степень многочленов
![]() ,т.е.
,т.е.
![]() =
max (n, m).
=
max (n, m).
Примечания:
-
При подстановке функции (28) в (27) приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения .
-
Формула (28) сохраняется и в случаях, когда
 .
. -
Если правая часть уравнения (24) есть сумма вида I или II то для нахождения у* следует использовать теорему о наложении решений.
Пример:
![]()
Найдем общее решение
![]() ЛОДУ
ЛОДУ
![]() ,
его характеристическое уравнение
,
его характеристическое уравнение
![]() имеет корень
имеет корень
![]() кратности 2. Значит
кратности 2. Значит
![]() .
Находим частное решение исходного
уравнения .В нем правая часть
.
Находим частное решение исходного
уравнения .В нем правая часть
![]() есть формула вида
есть формула вида
![]() ,
причем
,
причем
![]() не является корнем характеристического
уравнения
не является корнем характеристического
уравнения
![]() .
Поэтому , частное решение ищем как
частное решение уравнения (25) в виде
.
Поэтому , частное решение ищем как
частное решение уравнения (25) в виде
![]() ,т.е.
,т.е.
![]() ,
где A и B –
неопределенные коэффициенты .Тогда
,
где A и B –
неопределенные коэффициенты .Тогда
 .
Подставив
.
Подставив
![]() в исходное уравнение получим
в исходное уравнение получим
![]() ,
или
,
или
![]() .
Приравнивая коэффициенты при одинаковых
степенях
.
Приравнивая коэффициенты при одинаковых
степенях
![]() получаем систему уравнений
получаем систему уравнений
 ,
отсюда А=1,В=-2.
,
отсюда А=1,В=-2.
Поэтому частное решение данного уравнения
имеет вид
![]() .
Следовательно,
.
Следовательно,
![]() - искомое общее решение уравнения.
- искомое общее решение уравнения.
