2. Некоторые приложения степенных рядов

2.1. Приближенное вычисление значений функций

Пусть требуется вычислить значение функции при с заданной точностью . Если функцию в интервале можно разложить в степенной ряд и , то точное значение равно сумме этого ряда при , т.е. , а приближенное – частичной сумме , т.е. Точность этого равенства увеличивается с ростом , абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е. , где Таким образом, ошибку можно найти, оценив остаток ряда.

Для рядов лейбницевского типа . В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммировался. И в качестве оценки берут величину остатка этого нового ряда.

2.2. Приближенное вычисление определенных интегралов

Бесконечные ряды применяются для вычисления неопределенных и определенных интегралов в случае, когда первообразная не выражается в конечном виде через элементарные функции, либо нахождение первообразной сложно.

Пусть требуется вычислить с точностью до . Если подинтегральную функцию можно разложить в ряд по степеням x и интервал сходимости включает в себя отрезок , то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычисления определяют так же, как и при вычислении значений функции.

Пример. Вычислить интеграл 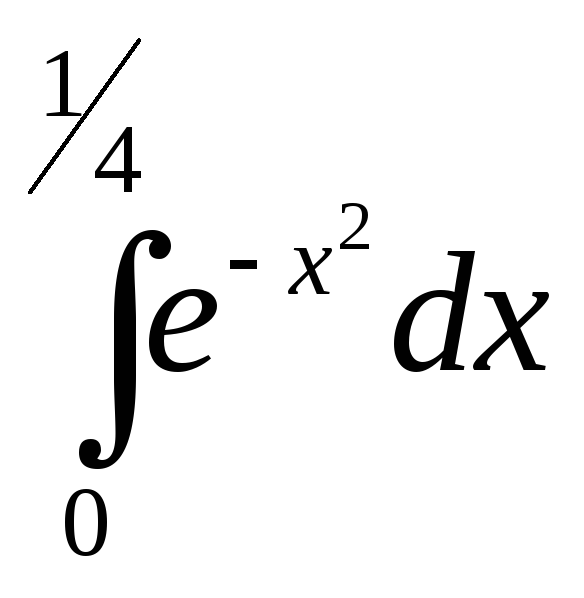с точностью до

Решение. Разложим подынтегральную функцию в ряд Макларена, заменяя x на (–x²) . Интегрируя обе части равенства на отрезке , лежащем внутри интервала сходимости , получим Получили ряд Лейбницевского типа. Так как , а , то с точностью до 0,001 имеем: .

VII. Ряды Фурье

7.1. Основные понятия

При изучении процессов, имеющих периодический характер, т.е. процессов, которые через определенный промежуток времени повторяются, более целесообразно разлагать функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд.

Напомним, что функция , определенная на множестве D, называется периодической с периодом T>0, если при каждом значение и выполняется равенство .

Для построения графика периодической функции периода T достаточно построить его на любом отрезке длины T и периодически продолжить его на всю область определения.

Отметим основные свойства периодической функции:

1. Алгебраическая сумма периодических функций, имеющих один и тот же период T есть периодическая функция с периодом T.

2. Если функция имеет период T, то функция имеет период : действительно, .

3. Если функция имеет период T и интегрируема на отрезке , то при любых и b.

Доказательство: пусть , тогда .

С другой стороны .

Но . Подставляя полученный результат, получим ч.т.д.

В частности, . Простейшими периодическими функциями являются тригонометрические функции и . Период этих функций равен 2π, т.е. . Простейшим периодическим процессом является простое гармоническое колебание, описываемое формулой

(1)

, где А – амплитуда колебаний, ω – частота, φ₀ – начальная фаза.

Функцию такого вида называют простой гармонической. Основным периодом этой функции является , т.е. одно полное колебание совершается за промежуток времени (а ω показывает, сколько колебаний совершает точка в течении 2π единиц времени).

Проведем преобразование этой функции (2), где

, .

Отсюда видно, что простое периодическое колебание описывается функциями и .

Сложное гармоническое колебание, возникающее в результате наложения конечного (или бесконечного) числа простых гармоник, также описывается функциями типа и.Так,функция или, что равносильно, функция задает сложное гармоническое колебание. Так как период первой гармонии есть , второй , третьей и т.д., а период функции (нулевая гармония) есть любое число, то функция имеет период, равный 2π, т.е. .

Понятно, что при наложении простых гармоник получаем периодическую функцию, описывающую сложное периодическое колебание (периодический процесс). Возникает вопрос: всякую ли периодическую функцию, описывающую периодический процесс, можно представить в виде суммы простых гармоник вида (1) и (2). Если да, то как найти неизвестные параметры каждой из этих гармоник? Ответим сначала на второй, а затем и на первый вопрос.