7.1. Вычисление площадей плоских фигур

Как уже говорилось выше площадь криволинейной трапеции, расположенной выше оси абсцисс , равна определенному интегралу или . Формула получена путем применения первого способа – метода сумм. Покажем, что именно это можно получить, используя приращение . При этом получит приращение , представляющее площадь элементарной криволинейной трапеции. в этом случае есть главная часть приращения при и, очевидно он равен произведению , как площади прямоугольника с высотой и с основанием .

Интегрируя полученное соотношение в пределах от до , получим . Если криволинейная трапеция расположена ниже оси , то ее площадь может быть найдена по формуле . Эти формулы можно объединить в одну . Площадь фигуры, ограниченной двумя кривыми и (рис.1) при условии и прямыми ; можно найти, используя соотношение: . Если плоская фигура имеет сложную форму, то прямыми, параллельными оси ее следует разбить на части так, ч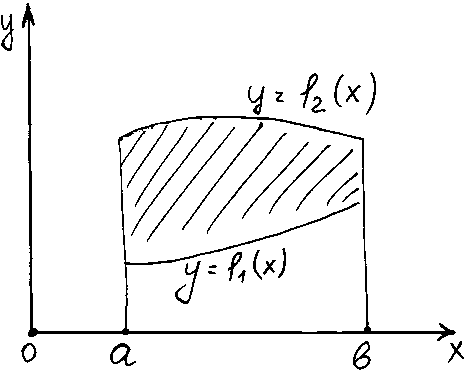тобы можно было применить выше записанные соотношения (рис.2). Если (Рис. 3.) криволинейная трапеция ограничена прямыми , , осью и кривой , то ее площадь находится по формуле . И, наконец, если криволинейная т

Рис.3.

рапеция ограничена кривой, з

Рис.1.

аданной п араметрически: , прямыми , и осью , то площадь ее находится по формуле: , где α и β определяются из равенств и .

7.2 Вычисление длины дуги плоской кривой

П

Рис.2.

Рис.4.

усть дана плоская кривая АВ, уравнение которой , где (рис.4). Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена стремится к нулю. Покажем, что если функция и ее производная непрерывны на отрезке , то кривая АВ имеет длину, равную . Применим способ №1. Для чего разобьем отрезок на n частей , каждой точке соответствуют точки , на кривой АВ. Проведем хорды , … длины которых обозначим соответственно через ∆L_1, ∆L₂…∆L_n. Получим ломаную линию M₀M₁…M_n, длина которой равна . Длину хорды (или звена ломаной) найдем по теореме Пифагора из треугольника с катетами ∆x_i и ∆y_i: , где , . По теореме Лагранжа о конечном приращении функции . Поэтому , а длина ломаной линии M₀M₁…M_n равна (1).

Длина ℓ кривой АВ по определению равна ℓ . Заметим, что при также и ( и, следовательно, ). Функция непрерывна на отрезке , так как по условию непрерывна функция . Следовательно, существует предел интегральной суммы, когда : ℓ . Таким образом,

ℓ или ℓ (2).

Если уравнение кривой задано в параметрической форме , где x(t) и y(t) – непрерывные функции с непрерывными производными и , , то длина ℓ находится по формуле: ℓ . Это соотношение получается из (2) путем подстановки , , .

Пример: Найти длину окружности радиуса R.

Если уравнение окружности записать в параметрической форме , то ℓ.

7.3 Вычисление объема тела

а) Вычисление объема тела по известным площадям параллельных сечений.

П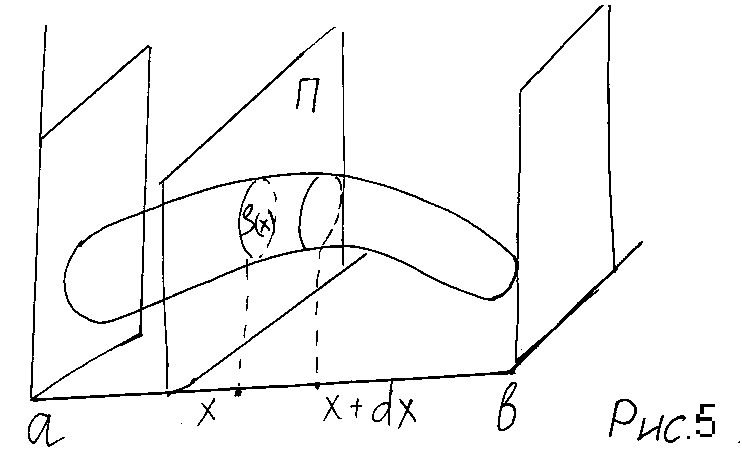усть требуется найти объем тела V при известной площади S сечений этого тела относительно плоскости, перпендикулярной некоторой оси, например, ох; . Применим метод 2.

Через произвольную точку проведем плоскость , перпендикулярную оси ох. Обозначим через площадь сечения тела этой плоскостью. считаем известной и изменяющейся непрерывно при изменении . Через v обозначим объем части тела, лежащие левее плоскости . Будем считать, что на отрезке величина v есть функция от , т.е. v = v (x)( v ()=0, v ()=v. Теперь найдем дифференциал функции v = v (x). Он представляет собой слой тела, заключенного между параллельными плоскостями, пересекающими ось в точках и , который можно приближено принять за цилиндр с основанием и высотой (рис.5). поэтому дифференциал объема . Тогда для нахождения полного объема это соотношение надо проинтегрировать в пределах от до .

- полученная формула называется формулой объема тела по площади параллельных сечений.

Пример: Найти объем эллипсоида . Если эллипсоид рассечен плоскостью, параллельной плоскости и на расстоянии от нее получим эллипс (см. рис. 6).

.

Площадь этого эллипса равна . Поэтому объем эллипсоида

б) Объем тела вращения

Пусть вокруг оси вращается криволинейная трапеция, ограниченная непрерывной линией отрезком и прямыми и . Полученная от вращения фигура, называется телом вращения. Сечение этого тела - плоскостью, перпендикулярной оси , проведенной через произвольную точку, есть круг радиуса . Следовательно, . Поскольку - выражение для объема тела вращения вокруг оси . Если криволинейная трапеция ограничена графиком непрерывной функции и прямыми при условии , то для объема тела, образованного вращением этой трапеции относительно оси , по аналогии с полученным выше можно записать:

в) Вычисление координат центра тяжести плоской фигуры

П

Рис. 8.

усть дана материальная плоская фигура (пластина), ограниченная кривой и прямыми (рис. 8). Будем считать, что плотность пластины есть величина . Тогда масса всей пластины равна , т.е. Выделим элементарный участок пластины в виде бесконечно малой узкой вертикальной полосы и будем считать его прямоугольником. Его масса равна . Центр тяжести прямоугольника лежит на пересечении диагоналей прямоугольника. Это точка отстоит от оси на расстоянии , а от оси на расстоянии . Тогда для элементарных статистических моментов относительно осей и получим следующие соотношения: и . Отсюда ; . Если обозначим координаты центра тяжести плоской фигуры то получим, что ;, т.е. или и .