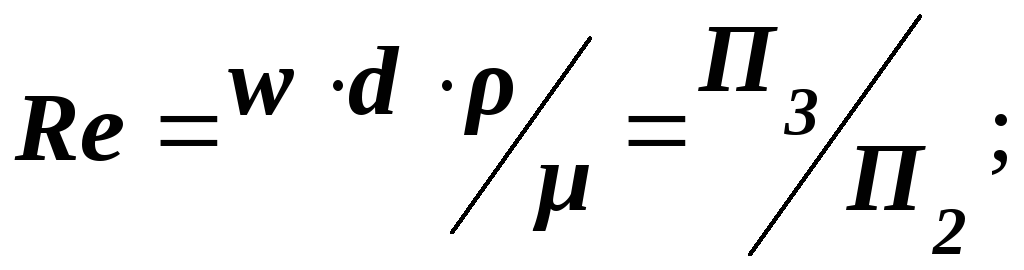Установление вида критериев на основе принципа однородности размерностей
Если функцию f(x1, x2, … xn) = 0 (4.19)
разложить в степенной ряд, то получим:
(4.20)
Все члены равенства (4.20) имеют одну и ту же размерность, а оно является однородной функцией относительно размерностей. В этом состоит принцип однородности размерностей.
Если все члены равенства (4.20) разделить, например, на первый член, то получим:
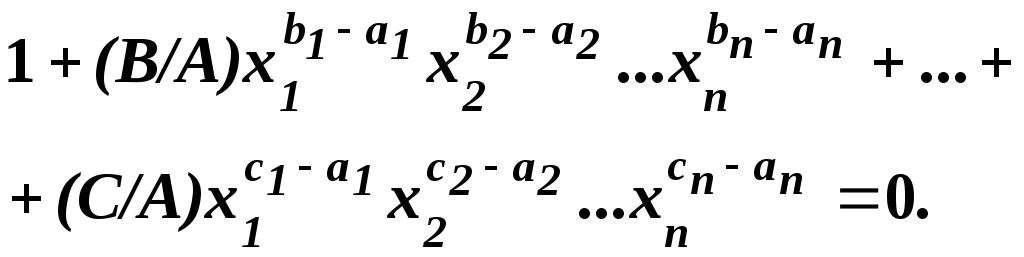(4.21)
В уравнении (4.21) все члены безразмерны, поэтому для любого члена этого уравнения справедливо соотношение:
(4.22)
где квадратные скобки служат для указания размерностей заключенных в них переменных, а степени αi1, αi2, … αin могут принимать следующие значения:
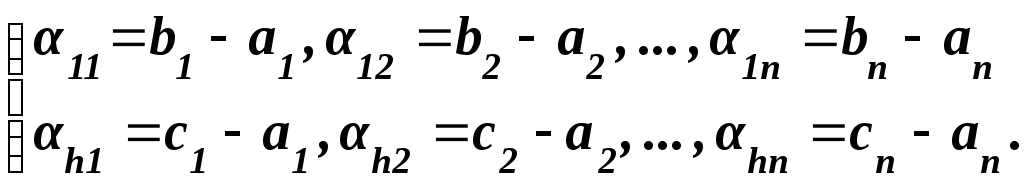(4.23)
Уравнение (4.23), вытекающее из принципа однородности размерностей, позволяет находить вид безразмерных критериев, с помощью которых можно описать изучаемую систему.
Запишем размерности названных выше величин в системе LMT (длина, масса, время):
– коэффициент массопередачи, LT-1;
l – характерный линейный размер обтекаемого тела, L;
ρ – плотность, ML-3;
D – коэффициент диффузии вещества, L2T-1;
– вязкость, ML-1T-1;
W –скорость потока, LT-1;
Для нашей задачи получаем:
(4.24)
Здесь П – некоторая безразмерная величина. Условие безразмерности П сводится к тому, что суммы показателей при первичных размерностях в левой части уравнения (4.24) должны быть равны нулю:
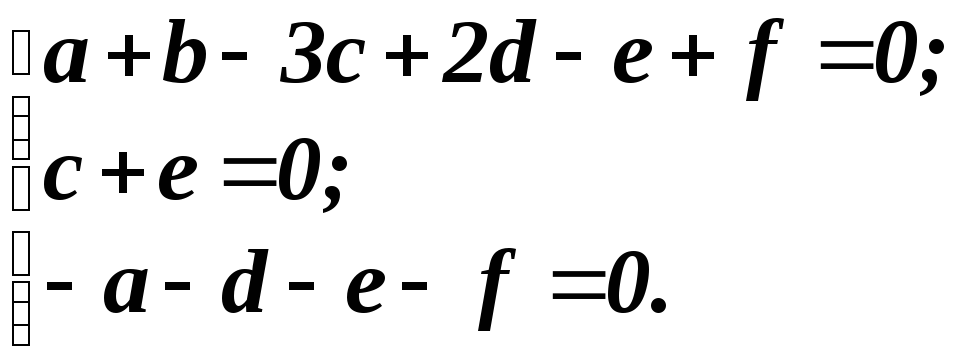
Здесь первое уравнение относится к показателю степени при L, второе – при M, третье – при T.
Выбрав за свободные переменные d, e и f, найдем, что:
a = – d – e – f;
b = – d – e;
c = – e.
Подставляя a, b и c в уравнение (4.24), предварительно заменив в нем члены на исходные переменные, получим:
β –d –e –f l–d –e ρ–e Dd μe W f = П. (4.25)
Сгруппируем в равенстве (4.25) члены с показателями d, e и f. Тогда:
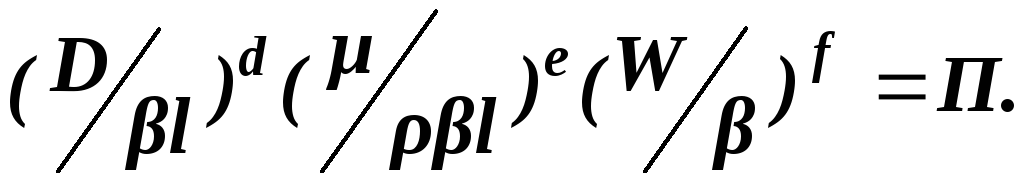(4.26)
Так как d, e и f – произвольные величины, то П может быть безразмерной величиной только в том случае, если каждое из выражений в скобках безразмерно.
Таким образом, мы получаем три безразмерных комплекса:
Установление вида критериев на основе модифицированной π-теоремы
Выберем в качестве первичных переменных , l и ρ. Вторичными переменными в данном случае будут D, и W. Общее число рассматриваемых переменных равно шести, число первичных – трем, следовательно, необходимо найти три безразмерных критерия: П1 , П2 , П3. Для их отыскания записываем отношения одной из вторичных переменных к произведению первичных переменных, причем каждую из первичных переменных берем в некоторой неизвестной степени. Затем вместо переменных в эту дробь подставляем их размерности, а неизвестные показатели степени находим, основываясь на том, что сам искомый критерий должен быть безразмерным.
В нашем случае:
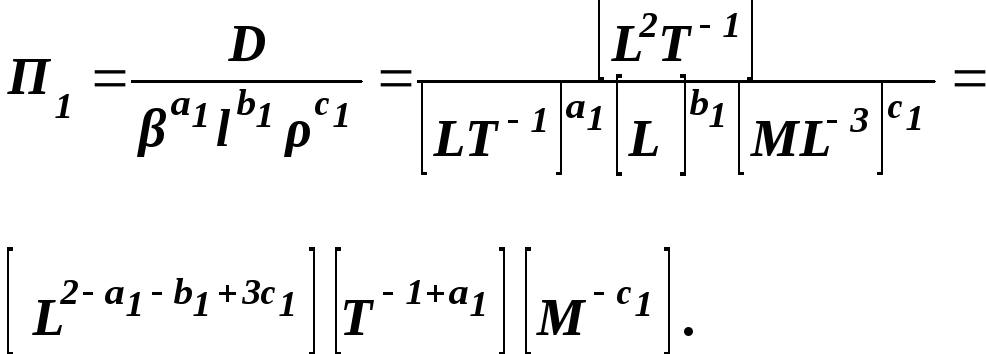(4.27)
Очевидно, что c1 = 0, a1 = 1, b1 = 1.
Таким образом:
(4.28)
Аналогично можно записать:
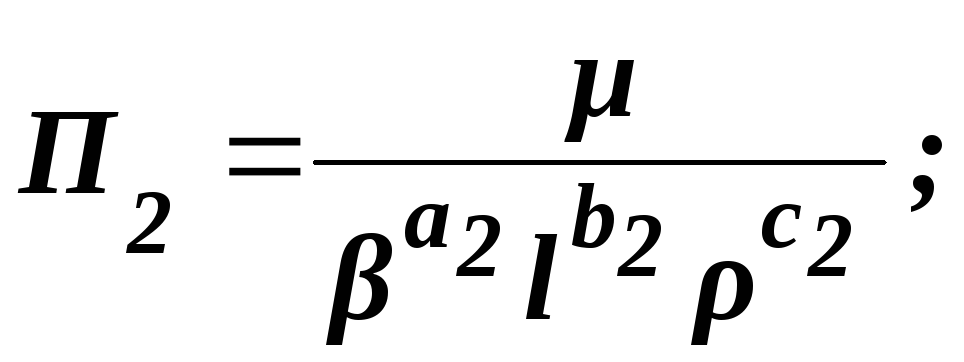(4.29)
|
|
(4.30) |
и найти, что:
|
|
(4.31) |
Заметим, что при решении практических задач вместо названных критериев пользуются широко известными критериями Нуссельта, Рейнольдса и Прандтля:
|
|
(4.32) |
|
|
|
|
|
(4.33) |
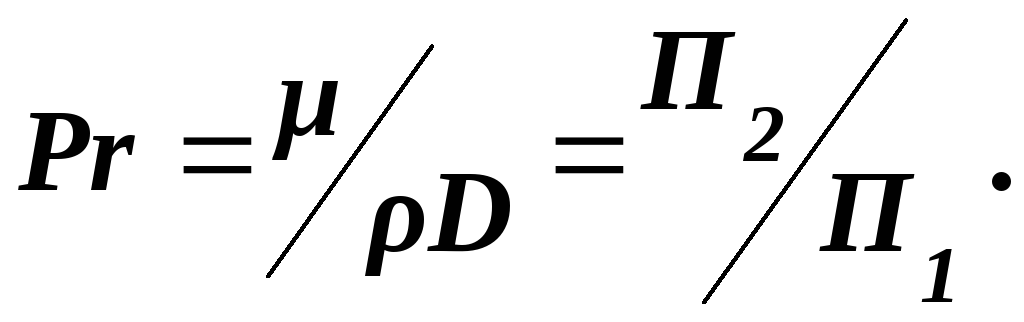(4.34)