2.4.3 Вираження мішаного добутку через координати.

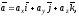
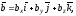
Нехай задані вектори 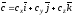. Знайдемо їхній мішаний добуток, використовуючи вираження в координатах для векторного і скалярного добутку :

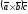
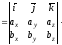
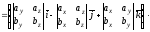
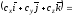
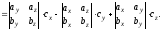(4.1)

Отриману формулу можна записати коротше:

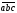
(4.2)

тому що права частина рівності (4.1) являє собою розкладання визначника третього порядку по елементах третього рядка.

Отже, мішаний добуток векторів дорівнює визначникові третього порядку, складеному з координат векторів, що перемножуються.

2.4.4. Деякі застосування мішаного добутку.

Визначення взаємної орієнтації векторів у просторі

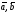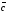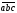
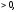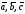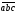
Визначення взаємної орієнтації векторів і засновано на наступних розуміннях. Якщо то - права трійка; якщо те 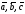- ліва трійка.

Встановлення компланарності векторів

Якщо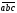=0 дорівнює нулеві

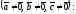
Вектори 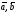і 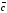компланарні тоді і тільки тоді, коли їхній мішаний добуток

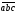
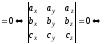вектори 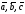- компланарні.

Визначення об'ємів паралелепіпеда і трикутної піраміди

Неважко показати, що об’єм паралелепіпеда, побудованого на векторах 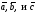обчислюється по формулі

,

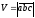а об’єм трикутної піраміди, побудованої на цих же векторах, дорівнює

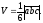
Приклад 4.1. Вершинами піраміди служать точк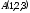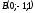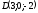и , , , . Знайти об'єм піраміди.

○ Знаходимо вектори :

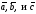Знаходимо :

=

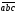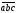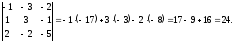
Отже, ●