- •Змістовий модуль 2 елементи векторної алгебри
- •Тема 2.1. Вектори.
- •2.1.1. Основні поняття .
- •2.1.2. Лінійні операції над векторами.
- •2.1.3. Проекція вектора на вісь.
- •2.1.4. Розкладання вектора по ортах координатних осей. Модуль вектора. Направляючі косинуси.
- •2.1.5. Дії над векторами, заданими проекціями.
- •Тема 2.2. Скалярний добуток вектора і його властивості.
- •2.2.1. Означення скалярного добутку.
- •2.2.2. Властивості скалярного добутку.
- •2.2.3. Вираження скалярного добутку через координати.
- •2.2.4. Деякі застосування скалярного добутку.
- •Тема 2.3. Векторний добуток вектора і його властивості.
- •2.3.1. Означення векторного добутку.
- •2.3.2. Властивості векторного добутку.
- •2.3.3. Вираження векторного добутку через координати.
- •2.3.4. Деякі застосування векторного добутку.
- •Тема 2.4. Мішаний добуток і його властивості.
- •2.4.1. Визначення мішаного добутку, його геометричний зміст.
- •2.4.2. Властивості мішаного добутку.
- •2.4.3 Вираження мішаного добутку через координати.
- •2.4.4. Деякі застосування мішаного добутку.
2.1.4. Розкладання вектора по ортах координатних осей. Модуль вектора. Направляючі косинуси.
Розглянемо
в просторі прямокутну систему координат
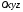 Виділимо
на координатних осях
Виділимо
на координатних осях
 ,
,
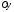 й
й
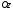 одиничні вектори (орти), що позначаються
одиничні вектори (орти), що позначаються
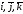 відповідно (див. рис.
11).
відповідно (див. рис.
11).
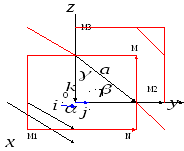
рис. 11.
Виберемо
довільний
вектор
 простору
і
сполучимо його початок з початком
координат:
простору
і
сполучимо його початок з початком
координат:
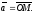
Знайдемо
проекції вектора
 на координатні осі.
на координатні осі.
Проведемо
через кінець вектора
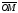 площини, паралельні координатним
площинам. Точки перетину – цих площин
з осями позначимо відповідно - через
площини, паралельні координатним
площинам. Точки перетину – цих площин
з осями позначимо відповідно - через
 і
і
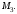 Одержимо прямокутний паралелепіпед,
однією з діагоналей якого є вектор
Одержимо прямокутний паралелепіпед,
однією з діагоналей якого є вектор
 .
Тоді
.
Тоді
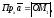
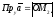
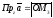 .
По означенню суми декількох векторів
знаходимо
.
По означенню суми декількох векторів
знаходимо

А тому що
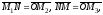 то
то
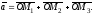 (1.1)
(1.1)
Але
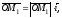
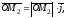
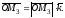 (1.2)
(1.2)
Позначимо проекції вектора
 на осі
на осі
 і
і
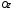 відповідно через
відповідно через
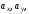 і
і
 тобто
тобто
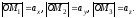 Тоді з рівності (1.1) і (1.2)
одержуємо
Тоді з рівності (1.1) і (1.2)
одержуємо
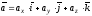 (1.3)
(1.3)
Ця
формула є основною у векторному численні
і називається розкладанням вектора по
ортах координатних осей. Числа
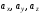 називаються координатами вектора
називаються координатами вектора
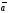 ,
тобто координати вектора є його проекції
на відповідні координатні осі.
,
тобто координати вектора є його проекції
на відповідні координатні осі.
Векторну
рівність (1.3)
часто записують у символічному виді:
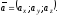
Рівність
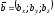 означає, що
означає, що

Знаючи
проекції вектора
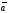 ,
можна легко знайти вираз для модуля
вектора. Спираючись на теорему про
довжину діагоналі прямокутного
паралелепіпеда, можна записати
,
можна легко знайти вираз для модуля
вектора. Спираючись на теорему про
довжину діагоналі прямокутного
паралелепіпеда, можна записати
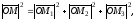 тобто
тобто
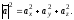 (1.4)
(1.4)
Звідси
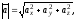
тобто модуль вектора дорівнює квадратному кореневі із суми квадратів його проект цій на осі координат.
Нехай
кути вектора
 з осями
з осями
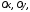 і
і
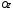 відповідно рівні
відповідно рівні
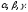 По властивості проекції вектора на
вісь, маємо
По властивості проекції вектора на
вісь, маємо
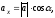
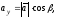
 (1.5)
(1.5)
Або, що те ж саме,
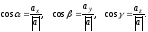
Числа
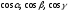 називаються направляючими косинусами
вектора
називаються направляючими косинусами
вектора
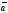 .
.
Підставимо вираз (1.5) у рівність (1.4), одержуємо
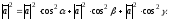
Скоротивши
на
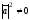 , одержимо співвідношення
, одержимо співвідношення
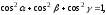
тобто сума квадратів направляючих косинусів ненульового вектора дорівнює одиниці.
Легко
помітити, що координатами
одиничного
вектора
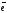 є
числа
є
числа
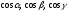 тобто
тобто

Отже, задавши координати вектора, завжди можна визначити його модуль і напрямок, тобто сам вектор.
2.1.5. Дії над векторами, заданими проекціями.
Нехай
вектори
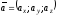 і
і
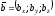 задані своїми проекціями на осі координат
задані своїми проекціями на осі координат
 або, що те ж саме
або, що те ж саме
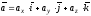 ,
,
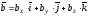
Лінійні операції над векторами
Тому що лінійні операції над векторами зводяться до відповідних лінійних операцій над проекціями цих векторів, то можна записати:
-
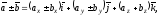 або
коротко
або
коротко
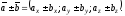
Тобто при додаванні (відніманні) векторів їхні однойменні координати додаються (віднімаються).
-
 або
коротше
або
коротше
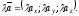
Тобто при множенні вектора на скляр координати вектора збільшуються на цей скляр.
Рівність векторів
З
означення вектора як напрямленого
відрізка, який можна пересувати в
просторі паралельно самому собі,
випливає, що два
вектори
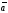 і
і
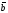 рівні тоді
і тільки тоді, коли виконуються рівності:
рівні тоді
і тільки тоді, коли виконуються рівності:
 тобто
тобто
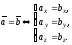
Колінеарність векторів
З'ясуємо
умови колінеарності векторів
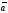 і
і
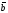 ,
заданих своїми координатами. Оскільки
,
заданих своїми координатами. Оскільки
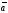 ║
║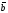 , то можна записати
, то можна записати
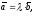 де
де
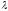 -
деяке число. Тобто
-
деяке число. Тобто
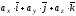
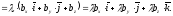
Звідси
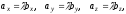
тобто
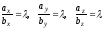 або
або

Таким чином, проекції колінеарних векторів пропорційні. Вірно і зворотне твердження: вектори, що мають пропорційні координати, колінеарні.
Координати точки
-
Нехай у просторі задана прямокутна декартова система координат
 Для будь-якої точки
Для будь-якої точки
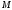 координати вектора
координати вектора
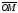 називаються координатами
точки
називаються координатами
точки
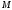 .
. -
Вектор
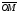 називається радіусом-вектором
точки
називається радіусом-вектором
точки
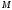 , позначається
, позначається
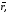 тобто
тобто
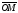

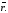 Отже, координати точки – це координати
її радіуса-вектора
Отже, координати точки – це координати
її радіуса-вектора
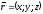 або
або
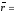
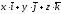 .
.
Координати
точки
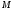 записуються у виді
записуються у виді

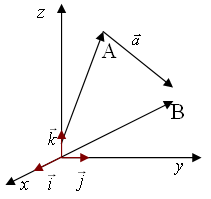
рис. 12.
Координати вектора
Знайдемо
координати вектора
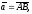 якщо відомі координати точок
якщо відомі координати точок
 і
і
 .
Маємо (див. рис.
12.):
.
Маємо (див. рис.
12.):
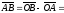

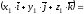
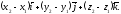
Отже,
координати вектора дорівнюють різниці
відповідних координат його кінця і
початку: