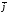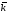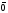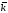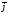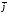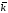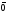- •Змістовий модуль 2 елементи векторної алгебри
- •Тема 2.1. Вектори.
- •2.1.1. Основні поняття .
- •2.1.2. Лінійні операції над векторами.
- •2.1.3. Проекція вектора на вісь.
- •2.1.4. Розкладання вектора по ортах координатних осей. Модуль вектора. Направляючі косинуси.
- •2.1.5. Дії над векторами, заданими проекціями.
- •Тема 2.2. Скалярний добуток вектора і його властивості.
- •2.2.1. Означення скалярного добутку.
- •2.2.2. Властивості скалярного добутку.
- •2.2.3. Вираження скалярного добутку через координати.
- •2.2.4. Деякі застосування скалярного добутку.
- •Тема 2.3. Векторний добуток вектора і його властивості.
- •2.3.1. Означення векторного добутку.
- •2.3.2. Властивості векторного добутку.
- •2.3.3. Вираження векторного добутку через координати.
- •2.3.4. Деякі застосування векторного добутку.
- •Тема 2.4. Мішаний добуток і його властивості.
- •2.4.1. Визначення мішаного добутку, його геометричний зміст.
- •2.4.2. Властивості мішаного добутку.
- •2.4.3 Вираження мішаного добутку через координати.
- •2.4.4. Деякі застосування мішаного добутку.
Тема 2.3. Векторний добуток вектора і його властивості.
2.3.1. Означення векторного добутку.
Три не
компланарних вектори
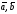 і
і
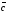 ,
узятих в зазначеному порядку, утворять
праву
трійку,
якщо з кінця третього вектора
,
узятих в зазначеному порядку, утворять
праву
трійку,
якщо з кінця третього вектора
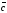 найкоротший поворот від першого вектора
найкоротший поворот від першого вектора
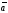 до другого вектора
до другого вектора
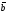 видний, що здійснюється проти годинникової
стрілки, і ліву, якщо по годинниковій
(див. рис.
15).
видний, що здійснюється проти годинникової
стрілки, і ліву, якщо по годинниковій
(див. рис.
15).

рис.15.
-
Векторним добутком вектора
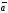 на вектор
на вектор
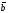 називається вектор
називається вектор
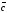 ,
що:
,
що:
-
перпендикулярний векторам
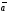 і
і
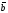 ,
тобто
,
тобто
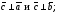
-
має довжину, чисельно рівну площі паралелограма, побудованого на векторах
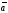 і
і
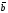 як на сторонах. (див. рис.
16),
тобто
як на сторонах. (див. рис.
16),
тобто

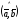 ;
;
-
вектори
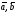 й
й
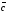 утворюють праву трійку.
утворюють праву трійку.
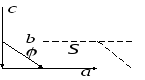


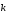


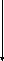






рис. 16. рис.17.
Векторний
добуток позначається
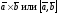 З означення векторного добутку
безпосередньо випливають наступні
співвідношення між ортами
З означення векторного добутку
безпосередньо випливають наступні
співвідношення між ортами
 (див. рис.17):
(див. рис.17):
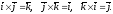
2.3.2. Властивості векторного добутку.
-
При перестановці співмножників векторний добуток змінює знак, тобто
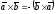 (див. рис.
18).
(див. рис.
18).
□ Вектори
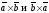 колінеарні, мають однакові модулі (площа
паралелограма залишається незмінної),
але протилежно спрямовані (трійки
колінеарні, мають однакові модулі (площа
паралелограма залишається незмінної),
але протилежно спрямовані (трійки
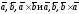 протилежної орієнтації). Стало бути,
протилежної орієнтації). Стало бути,
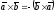 .■
.■
-
Векторний добуток має сполучну властивість щодо скалярного множника, тобто
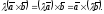

рис.18.
□ Нехай
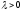 .
Вектор
.
Вектор
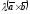 перпендикулярний векторам
перпендикулярний векторам
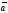 і
і
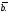 Вектор
Вектор
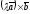 також перпендикулярний векторам
також перпендикулярний векторам
 і
і
 (вектори
(вектори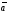 ,
,
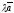 лежать в одній площині). Виходить вектори
лежать в одній площині). Виходить вектори
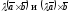 колінеарні. Очевидно, що і напрямку їх
збігаються. Мають однакову довжину:
колінеарні. Очевидно, що і напрямку їх
збігаються. Мають однакову довжину:
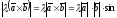
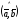
і

 =
=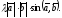
Тому
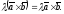 Аналогічно доводиться при
Аналогічно доводиться при
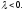 ■
■
-
Два ненульових вектори
 і
і
 колінеарні тоді і тільки тоді, коли
їхній векторний добуток дорівнює
нульовому векторові, тобто
колінеарні тоді і тільки тоді, коли
їхній векторний добуток дорівнює
нульовому векторові, тобто
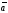 ║
║
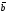
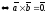
□ Якщо
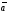 ║
║
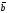 ,
то кут між ними дорівнює 0
,
то кут між ними дорівнює 0 або 180
або 180 . Але тоді
. Але тоді
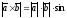
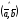
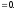 Виходить,
Виходить,
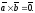
Якщо ж
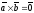 ,
то
,
то
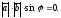 Але тоді
Але тоді
 або
або
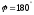 ,
тобто
,
тобто
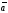 ║
║
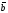 .■
.■
-
Зокрема,
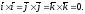
-
Векторний добуток має розподільну властивість:

Приймемо без доведення.
2.3.3. Вираження векторного добутку через координати.
Ми будемо
використовувати таблицю векторного
добутку векторів
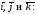
|
|
|
|
|
|
|
|
|
- |
|
|
- |
|
|
|
|
|
- |
|
Щоб не помилитися з знаками користуйтеся схемою:

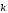





![]()
якщо напрямок найкоротшого шляху від першого вектора до другого збігається з напрямком стрілки, то добуток дорівнює третьому векторові, якщо не збігається — третій вектор береться зі знаком «мінус».
Нехай
задані два вектори
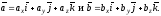 Знайдемо векторний добуток цих векторів,
перемножуючи їх як багаточлени (згідно
властивостей векторного добутку):
Знайдемо векторний добуток цих векторів,
перемножуючи їх як багаточлени (згідно
властивостей векторного добутку):

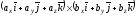

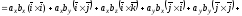
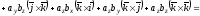
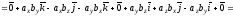
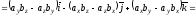

тобто
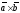
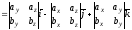 (3.1)
(3.1)
Отриману формулу можна записати ще коротше:
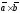
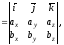 (3.2)
(3.2)
тому що права частина рівності (3.1) відповідає розкладанню визначника третього порядку по елементах першого рядка. Рівність (3.2) легко запам'ятовується.