
- •Оглавление
- •Преподавателю: как использовать это пособие
- •Тому, кто хочет научиться
- •Введение
- •Сводная таблица условий задачи о дневном рационе
- •Построение модели
- •1 Этап. Определение переменных, для которых будет составляться математическая модель.
- •2 Этап. Формирование целевой функции.
- •3 Этап. Формирование системы ограничений.
- •Нахождение решения задачи о дневном рационе средствами Microsoft Excel
- •Формулы, описывающие ограничения модели
- •Решение задачи о выпуске продукции
- •Постановка задачи
- •Сводная таблица
- •Построение модели
- •1 Этап. Определение переменных, для которых будет составляться математическая модель.
- •2 Этап. Формирование целевой функции.
- •3 Этап. Формирование системы ограничений.
- •Нахождение решения задачи о выпуске продукции средствами Microsoft Excel
- •Резюме:
- •Контрольные задания
- •Контрольное задание №1
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вопросы для самоконтроля
- •Лабораторная работа 2 Анализ чувствительности задач линейного программирования
- •Теоретическая часть
- •Анализ оптимального решения на чувствительность в Excel
- •Исходные данные
- •Резюме:
- •Контрольные задания
- •Вопросы для самоконтроля
- •Лабораторная работа 3 Решение транспортной задачи
- •Теоретическая часть
- •Общий вид транспортной матрицы
- •Решение транспортных задач
- •Решение сбалансированной транспортной задачи
- •Исходные данные транспортной задачи (транспортная матрица)
- •Построение модели
- •Нахождение решения транспортной задачи в Microsoft Excel
- •Формулы экранной формы задачи
- •Решение несбалансированной транспортной задачи
- •Транспортные расходы по доставке муки (руб./т)
- •Построение модели
- •1 Шаг. Определение переменных
- •2 Шаг. Проверка сбалансированности задачи
- •3 Шаг. Построение сбалансированной транспортной матрицы
- •Транспортная матрица задачи
- •4 Шаг. Задание целевой функции
- •5 Шаг. Задание ограничений
- •Нахождение решения транспортной задачи в Microsoft Excel
- •Формулы экранной формы задачи
- •Резюме:
- •Контрольное задание
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вопросы для самоконтроля
- •Лабораторная работа 4 Решение задачи о назначениях
- •Теоретическая часть
- •Общий вид транспортной матрицы задачи о назначениях
- •Решение задачи о назначениях
- •Постановка задачи о назначениях
- •Компетентность новых сотрудников
- •Компетентность прежних сотрудников
- •Рекомендации к решению задачи о назначениях
- •Построение модели для задачи
- •Транспортная матрица задачи о назначениях
- •1 Шаг. Определение переменных
- •2 Шаг. Проверка сбалансированности задачи
- •3 Шаг. Построение сбалансированной транспортной матрицы
- •Сбалансированная транспортная матрица задачи о назначениях
- •4 Шаг. Задание целевой функции
- •5 Шаг. Задание ограничений
- •Нахождение решение задачи о назначениях средствами Excel
- •Контрольное задание
- •Номера сотрудников и мест их работы для конкретного варианта
- •Компетентность новых сотрудников
- •Компетентность прежних сотрудников
- •Вопросы для самоконтроля
- •Лабораторная работа 5 Организация оптимальной системы снабжения
- •Постановка задачи
- •Рекомендации к решению задачи
- •Построение модели и решение задачи
- •Параметры перевозок из оптовых баз к потребителям
- •Параметры перевозок от изготовителей к оптовым базам
- •Параметры перевозок от изготовителей к потребителям
- •Транспортная матрица для способа №1
- •Сбалансированная транспортная матрица для способа №1
- •Контрольное задание
- •Параметры перевозок из оптовых баз к потребителям
- •Параметры перевозок от изготовителей к оптовым базам
- •Параметры перевозок от изготовителей к потребителям
- •Вопросы для самоконтроля
- •Литература
Вариант 10
-
Поставщики и их запасы
Потребители и потребительский спрос
B1
B2
B3
B4
35
35
45
30
A1
40
3
2
4
1
A2
50
2
3
1
5
A3
55
3
2
4
5
Таблица 34
Вариант 11
-
Поставщики и их запасы
Потребители и потребительский спрос
B1
B2
B3
B4
10
15
9
11
A1
10
2
3
5
7
A2
15
3
4
8
6
A3
20
1
6
3
21
Таблица 35
Вариант 12
-
Поставщики и их запасы
Потребители и потребительский спрос
B1
B2
B3
B4
20
30
30
10
A1
30
2
3
2
4
A2
40
3
2
5
1
A3
20
4
3
2
6
-
Вопросы для самоконтроля
-
Что такое транспортная задача?
-
Какова постановка стандартной ТЗ?
-
Запишите математическую модель ТЗ.
-
Перечислите исходные и искомые параметры модели ТЗ.
-
Раскройте понятие сбалансированности ТЗ.
-
Что такое фиктивные и запрещающие тарифы?
-
В каком соотношении должны находиться величины фиктивных и запрещающих тарифов при необходимости их одновременного использования в транспортной модели?
Лабораторная работа 4 Решение задачи о назначениях
Выполнив эту работу, Вы сможете:
-
научиться строить математическую модель для задачи о назначениях;
-
освоить технологию задач о назначениях в табличном редакторе Microsoft Excel.
-
Теоретическая часть
![]() Задача
о назначениях – это распределительная
задача, в которой для выполнения каждой
работы требуется один и только один
ресурс (один человек, одна автомашина
и т.д.), а каждый ресурс может быть
использован на одной и только одной
работе.
Задача
о назначениях – это распределительная
задача, в которой для выполнения каждой
работы требуется один и только один
ресурс (один человек, одна автомашина
и т.д.), а каждый ресурс может быть
использован на одной и только одной
работе.
Это означает, что ресурсы не делимы между работами, а работы не делимы между ресурсами. Таким образом, задача о назначениях является частным случаем транспортной задачи. Задача о назначениях имеет место при назначении людей на должности или работы, автомашин на маршруты, водителей на машины, при распределении групп по аудиториям, научных тем по научно-исследовательским лабораториям и т.п. Рассмотрим несколько практических примеров.
Пример 1.
Выпускники военной академии получают назначения на места службы. Каждый офицер имеет определенные пожелания относительно места службы. В свою очередь, в зависимости от места службы определенные требования предъявляются к офицеру. Желательно заполнить все вакантные места. Необходимо найти наилучшие (с точки зрения обеих сторон) назначения.
Пример 2.
Большая фирма переезжает в новое здание. Возникает необходимость распределить сотрудников по помещениям. С одной стороны, каждый сотрудник выдвигает определенные требования к своим соседям (например, предпочитает некурящих) и к расположению комнаты (например, вблизи от коллег по совместному проекту). С другой стороны, каждое помещение имеет определенные характеристики. Необходимо найти такой вариант распределения, при котором, по меньшей мере, не ухудшился бы психологический климат в коллективе.
Исходные параметры модели:
-
n – количество ресурсов, m – количество работ.
-
 – единичное количество ресурса
– единичное количество ресурса
 (
( ),
например: один работник; одно транспортное
средство; одна научная тема и т.д.
),
например: один работник; одно транспортное
средство; одна научная тема и т.д. -
 – единичное количество работы
– единичное количество работы
 (
( ),
например: одна должность; один маршрут;
одна лаборатория.
),
например: одна должность; один маршрут;
одна лаборатория. -
 – характеристика качества выполнения
работы
– характеристика качества выполнения
работы
 с помощью ресурса
с помощью ресурса
 .
Например, компетентность i-го
работника при работе на j-й
должности; время, за которое i-е
транспортное средство перевезет груз
по j-му маршруту; степень
квалификации i-й лаборатории
при работе над j-й научной
темой.
.
Например, компетентность i-го
работника при работе на j-й
должности; время, за которое i-е
транспортное средство перевезет груз
по j-му маршруту; степень
квалификации i-й лаборатории
при работе над j-й научной
темой.
Искомые параметры модели задачи о назначениях
-
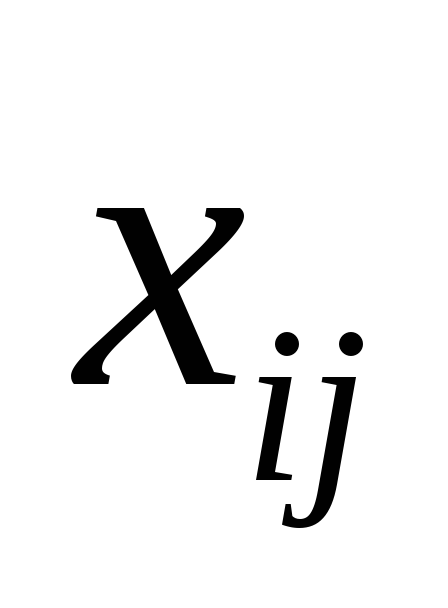 – факт назначения или неназначения
ресурса
– факт назначения или неназначения
ресурса
 на работу
на работу
 :
:

-
 – общая (суммарная) характеристика
качества распределения ресурсов по
работам.
– общая (суммарная) характеристика
качества распределения ресурсов по
работам.
Таблица 36
