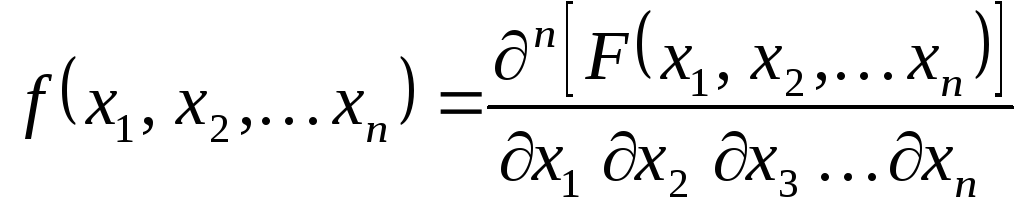Косвенные оценки качества.

Косвенные оценки качества проводятся чаще всего по АЧХ.

Пусть АЧХ некоторой системы имеет вид:

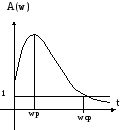
1. резонансная частота – определяется как частота в которой АЧХ достигает своего максимального значения .

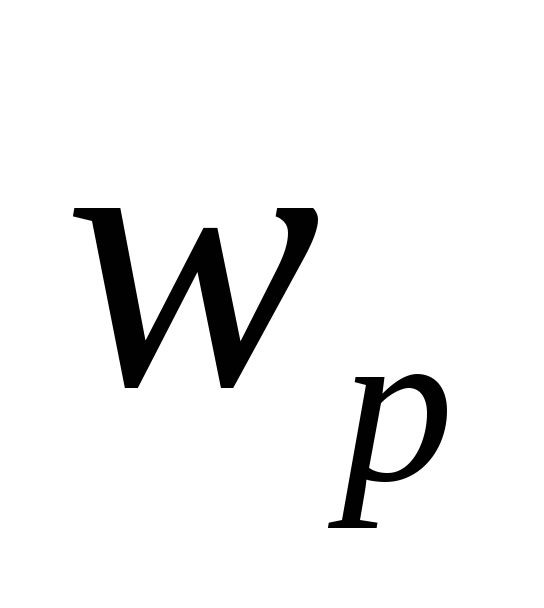2. показатель колебательности – определяется как отношение амплитуд:

3. частота среза – частота при которой АЧХ достигает значения, равного 1.

Частота среза косвенно характеризует длительность переходного процесса. Чем меньше частота среза, тем больше время переходного процесса.

Вопросы для самоконтроля.

1. Суть критерия устойчивости Ляпунова.

2. Косвенные оценки качества систем.

3. Прямые оценки качества систем.

Лекция 8 математическое описание стохастических систем.

Цель. Изучить способы математического описания стохастических систем.

Задачи:

1. Изучить понятие случайной величины и случайного процесса.

2. Изучить понятие плотности и функции распределения вероятности случайной величины.

3. Изучить статистические оценки случайных величин и процессов.

Случайные процессы в линейных динамических системах.

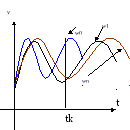
Случайная функция или случайный процесс – это процесс в котором выходная функция в результате опытов принимает некоторые случайные значения. В этом случае случайная функция «у» будет являться функцией аргумента t и некоторого опыта w.

При некотором фиксированном значении w=w₀, получим процесс, являющийся реализацией случайного процесса .

Если зафиксировать некоторый момент времени, то получим некоторое событие . Фиксируя различные моменты времени, получим последовательность событий ,являющихся n-мерной случайной функцией.

Каждое из событий будем обозначать в виде:

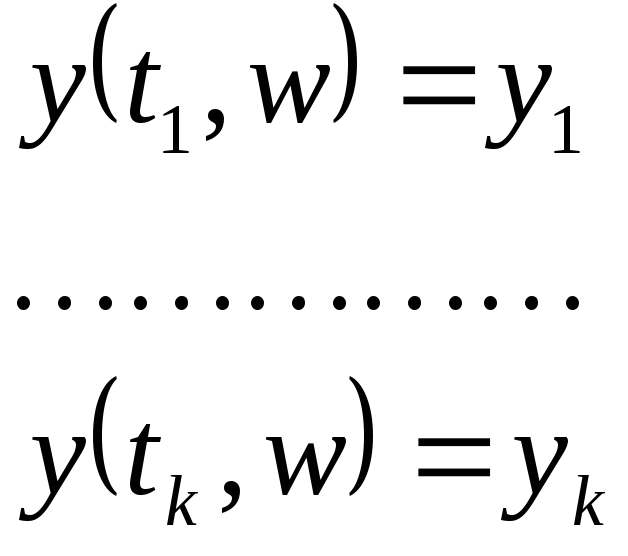
Рассмотрим некоторую непрерывную случайную величину. Пусть случайная величина принимает значения на интервале (a,b). Обозначим вероятность того, что случайная величина «у» принимает значения меньше некоторого зафиксированного заданного «У» через F(y).

F(y) – называется функцией распределения случайной величины. Эта функция задает для всех значений «у» значение вероятности, .

Свойства функции распределения вероятности:

1. Значение функции распределения вероятности принадлежит .

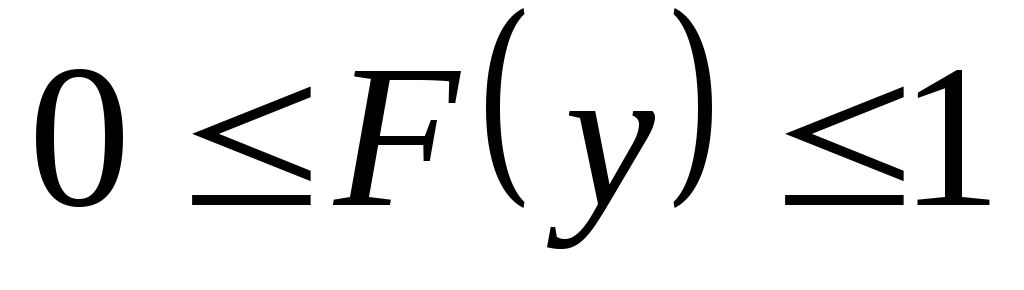2. Функция распределения вероятности есть величина неубывающая:

3. Если все значения случайной величины принадлежат отрезку [a,b], то для y<a 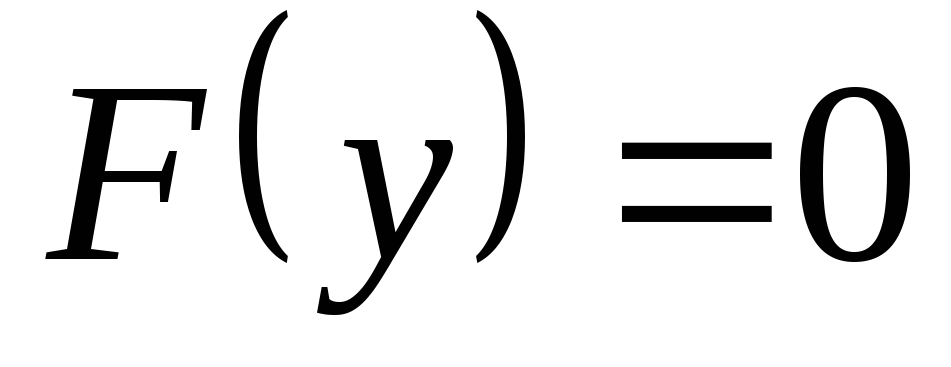, а дляy>b .

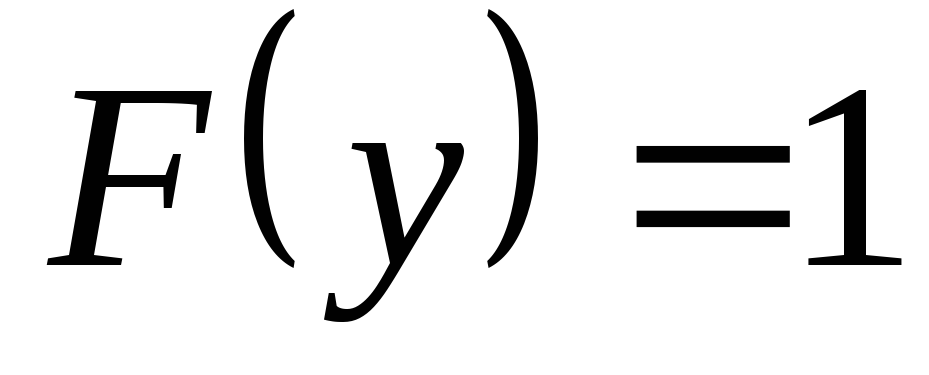4. Вероятность того, что случайная величина примет значение из отрезка [a,b], называется приращением функции распределения вероятности.

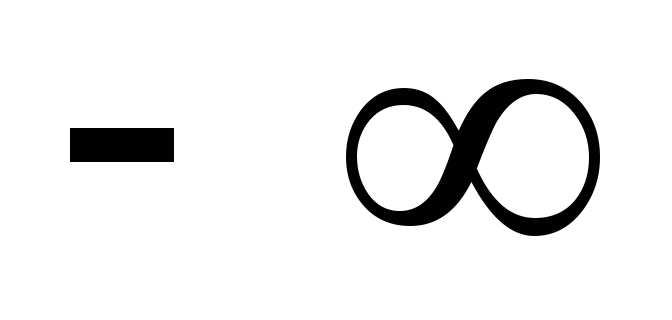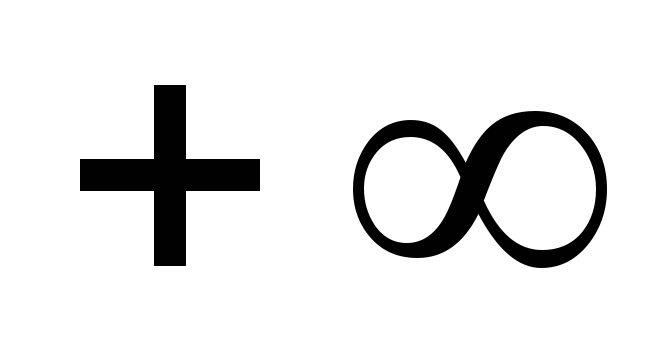5. Если случайная величина принимает значения на всей числовой оси от до, то:

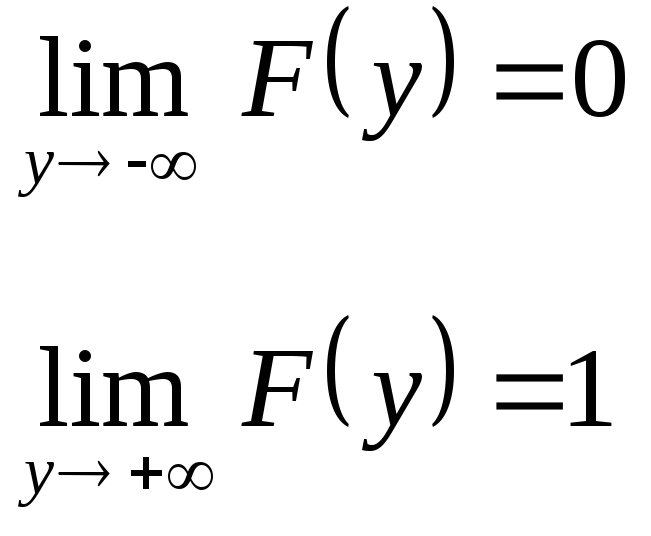
Плотность распределения вероятности.

Если функция распределения вероятности F(y) дифференцируема, то ее можно представить в виде:

Функция

Если она существует, то она называется плотностью распределения вероятностей случайной величины.

Свойства.

1. Плотность распределения вероятностей есть величина неотрицательная.

2. 

3. 

Функция и плотность распределения вероятности для дискретной случайной величины.

Дискретная случайная величина – это величина, значение которой определено лишь в некоторые моменты времени .

Дискретная случайная величина обозначается .

Функция распределения вероятности некоторой дискретной случайной величины:

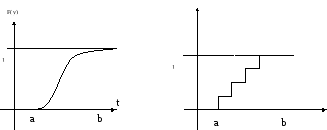
На любом интервале значение функции распределения вероятности не изменяется. В точке k происходит разрыв функции и величина скачка определяется вероятностью Р_k .

Определим плотность распределения вероятности для дискретной случайной величины:

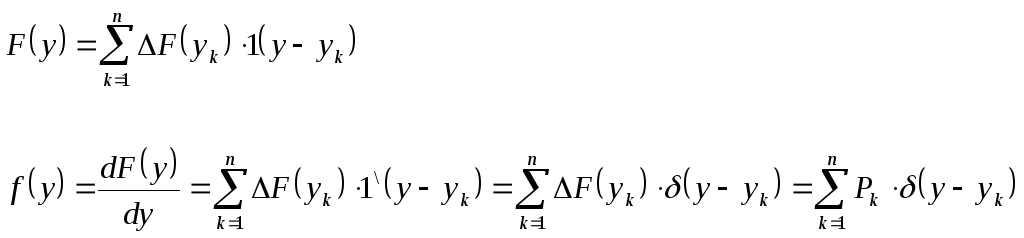
Многомерные случайные величины.

Представим входной сигнал в виде вектора , а выходной:

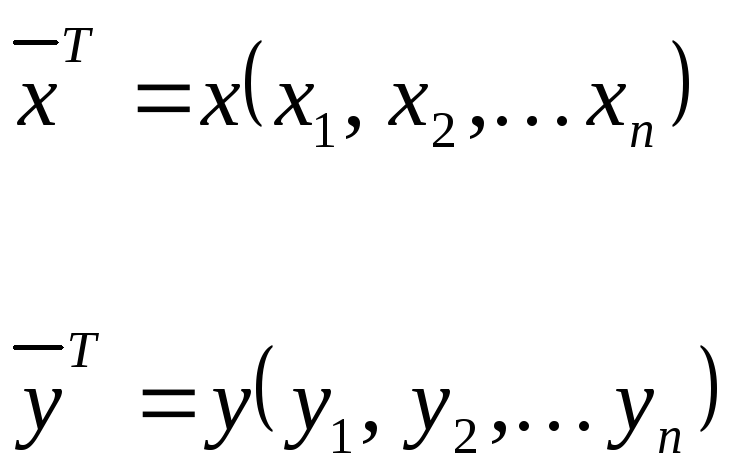
Тогда система примет вид:

Составляющие вектора иявляются некоторыми функциями реализации w:

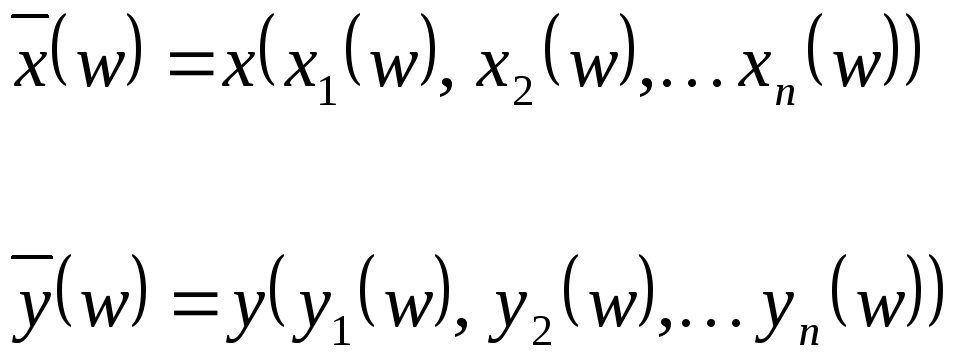
Многомерная случайная величина – это векторная функция, заданная на множестве элементарных событий или реализаций и каждое ее возможное значение является также вектором.

Функция распределения вероятности многомерной случайной величины определяется вероятностью того, что:

.

Плотность распределения вероятности многомерной случайной величины определяется как частная производная порядка n.