Лекция 9. Стационарные случайные функции или процессы.

Цель. Изучение стационарных и эргодических случайных процессов

Задачи:

1. Изучить характеристики стационарных случайных процессов

2. Изучить характеристики эргодических случайных процессов

3. Изучить прохождение случайного сигнала через непрерывную систему.

Случайные функции, для которых все n-мерные функции распределения вероятностей не изменяются в зависимости от начала отсчета времени, то есть выполняется равенство:

называются стационарными в узком смысле.

Аналогичное равенство справедливо и для плотности распределения вероятностей:

Для непрерывной величины случайная функция с постоянным математическим ожиданием и корреляционной функцией, не зависящей от момента времени t₁ и t₂, а зависящей только от разности аргументов, то есть выполняется равенство:

называется стационарной функцией в широком смысле.

Для дискретной величины должно выполняться условие:

Две случайные функции x(t) и y(t) называются стационарно связанными, если их взаимная корреляционная функция не зависит от аргументов, а зависит только от их разности.

Для стационарных процессов справедливо равенство:

Для двух дискретных процессов «х» и «у» для их стационарности должно выполняться равенство:

Эргодические случайные функции или процессы.

Стационарный процесс, для которого статистические характеристики, полученные усреднениями одной реализации на достаточно длительном промежутке времени, совпадают с достаточной степенью точности с усреднением множества реализации в фиксированный момент времени, называются эргодическими.

Случайная функция называется эргодической по отношению к математическому ожиданию, если выполняется условие:

- усреднение одной реализации и совпадает с усреднением по множеству реализаций:

Случайная функция называется эргодической по отношению к дисперсии, если выполняется равенство:

- одна реализация,

- множество реализаций.

Случайный процесс называется эргодическим по отношению к корреляционной функции, если выполняется равенство:

Для дискретных случайных процессов, эргодичных по отношению математическому ожиданию, справедливо следующее равенство:

Дискретная случайная функция называется эргодической по отношению к дисперсии, если выполняется равенство:

Некоторый дискретный случайный процесс называется эргодическим по отношению к корреляционной функции, если выполняется равенство:

Прохождение случайного сигнала через линейную непрерывную систему.

Рассмотрим систему, на которую действует случайный сигнал . Весовая функция этой системы или элемента, тогда случайный выходной сигналможно определить:

Если для входного случайного сигнала заданы математическое ожидание и корреляционная функция, то можно определить числовые характеристики выходного сигнала:

1. Математическое ожидание выходного сигнала:

Применим операцию математического ожидания для левой и правой части [1].

2. Определим корреляционную функцию выходного сигнала. Для этого из [1] вычтем [2].

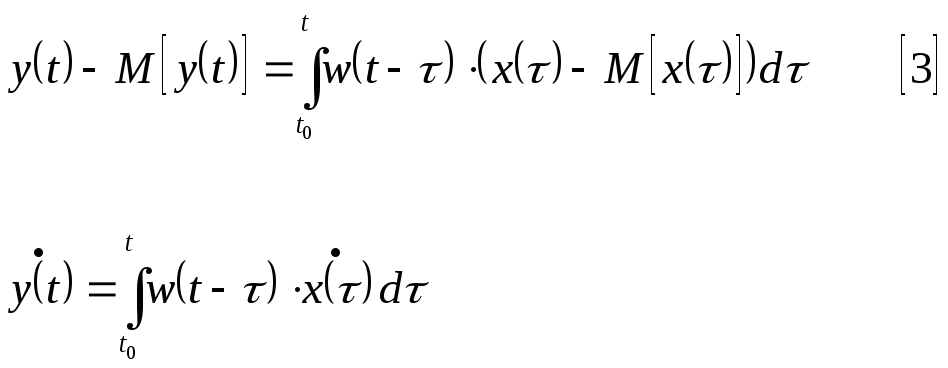
Запишем полученное выражение для момента времени t₁ и t₂,

Применим к левой и правой части операцию математического ожидания.

Дисперсия выходного сигнала:

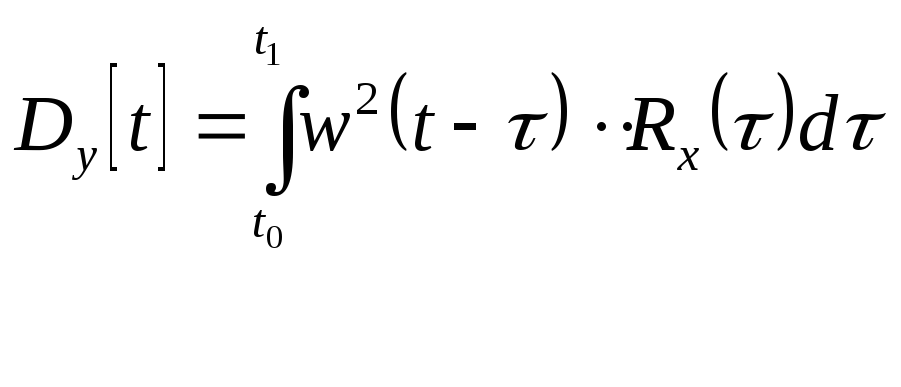
4. Взаимная корреляционная функция:

определяется аналогично.

Вопросы для самоконтроля.

1. Понятие стационарности в узком смысле.

2. Понятие стационарности в широком смысле.

3. Условие эргодичности процесса по отношению к математическому ожиданию.

4. Условие эргодичности процесса по отношению к дисперсии.

5. Условие эргодичности процесса по отношению к корреляционной функции.

6. Вывод взаимной корреляционной функции.

54