Лекция 5. Математическое описание дискретных динамических систем или элементов.

Цель. Изучить математическое описание дискретных динамических объектов.

Задачи:

1. Изучить понятия цифровых и импульсных систем.

2. Изучить математическое описание дискретных систем.

3. Рассмотреть способы квантования и модуляции сигналов.

4. Определить понятия решетчатой функции и разностных уравнений.

При математическом описании реальных систем управления необходимо описывать элементы являющиеся дискретными. В этих элементах входной сигнал изменяется не непрерывно, а скачками. В этом случае происходит квантование сигнала. Выделяют следующие виды квантования.

1). Квантование по уровню.

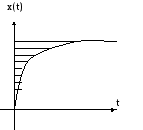
В этом случае амплитуда входного сигнала разбивается на равные интервалы. Исходная непрерывная функция x(t) заменяется последовательностью ленточных функций, зафиксированных на соответствующие уровни.

2). Квантование по времени.

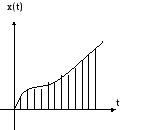
В этом случае на оси времени выделяются равные промежутки и исходная непрерывная функция заменяется последовательностью импульсов конечной длительности, площади которых совпадают со значением непрерывной функции в этот момент времени.

3). Цифровое квантование.

В этом случае исходная непрерывная функция заменяется набором приближенных значений, определенных в узлах сетки, построенной следующим способом: на оси времени откладываются равные промежутки на оси значений – функции, равные значениям амплитуды.

Элементы, в которых осуществляется квантование по уровню, называются релейными, соответственно САУ, содержащие такие элементы – релейные.

Элементы, в которых осуществляется квантование по времени, называются импульсными.

Элементы, осуществляющие квантование по уровню и по времени, называются цифровыми.

При математическом описании релейных и цифровых систем, используются нелинейные уравнения. При описании импульсных систем могут использоваться как линейные нелинейные, так и линейные уравнения. При исследовании систем, описываемых нелинейными уравнениями необходимо использовать или специальные методы анализа или приводить нелинейные уравнения к линейным, а затем исследовать их как линейные системы.

Рассмотрим импульсные системы. В них кроме импульсного элемента, содержится непрерывные элементы, которые можно объединить в непрерывную часть.

Импульсная модуляция заключается в изменении одного из параметров входного сигнала: амплитуды (А), времени импульса (t), периода следования импульсов (Т). В соответствии с этим различают амплитудно-импульсную, широтно-импульсную и частотно-импульсную модуляции.

1). Амплитудно-импульсная модуляция.

В этом случае время импульса и период следования являются величинами постоянными, а амплитуда – переменной.

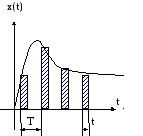
2). Широтно-импульсная модуляция.

В этом случае амплитуда импульса и период следования являются величинами постоянными, а время следования импульса – переменной.

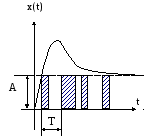
3). Частотно-импульсная модуляция.

В этом случае амплитуда импульса и время следования являются величинами постоянными, а период следования импульса – переменной.

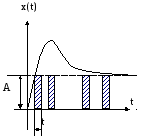
При различных видах модуляции, значению непрерывной функции пропорционально: амплитуда (АИМ);время (ШИМ);период (ЧИМ).

При использовании ЧИМ и ШИМ применяются нелинейные элементы, а при АИМ могут использоваться как нелинейные, так и линейные элементы, поэтому в дальнейшем дальше будем рассматривать амплитудно-импульсную модуляцию.

При АИМ импульсный элемент работает как некоторый ключ, замыкающийся на время импульса t, и в момент замыкания значение модулируемого сигнала совпадает со значением непрерывного сигнала и этот процесс повторяется с периодом Т. В том случае, когда t<<Т, последовательность получаемых импульсов можно представить в виде последовательности δ импульсов.

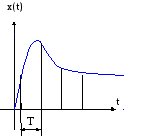
Импульсный элемент, осуществляющий модуляцию δ импульсами, называется идеальным импульсным элементом. Идеальные импульсы – это импульсы бесконечно малой длительности, бесконечно большой амплитуды, площади которых совпадают со значениями непрерывной функции .

При математическом описании реального импульсного элемента, его представляют в виде идеального импульсного элемента и формирователя импульсов.

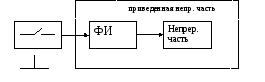
Формирователь импульсов преобразует идеальный импульс в импульс заданной формы и, является непрерывным элементом, который можно объединить с непрерывной частью. В результате получим приведенную непрерывную часть. Для упрощения математического описания импульсных систем, включающих в себя как импульсные, так и непрерывные элементы, все непрерывные сигналы представляются в виде фиктивных импульсных сигналов. В этом случае дифференциальные уравнения, используемые для описания непрерывных систем, заменяются разностными уравнениями. Непрерывные преобразования Лапласа заменяются дискретными преобразованиями Лапласа. Возможность такой замены основана на том, что выходной сигнал импульсного элемента определяется значениями непрерывного входного сигнала в дискретные моменты времени, соответствующие началу периода следования импульсов. Следовательно, в работе импульсного элемента ничего не изменится, если заменить входной непрерывный сигнал x(t), сигналом, определенным в моменты времени (nТ). В результате получим дискретный сигнал x(nТ), который совпадает со значением сигнала x(t) в моменты времени (nТ), и равный 0 в остальные моменты времени. Функция x(nt), описывающая такой сигнал называется решетчатой функцией, и исходный непрерывный сигнал будет являться огибающей для решетчатой функции.

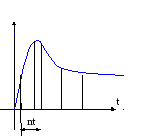
Функция называется смещенной решетчатой функцией и определяет поведение непрерывной функции внутри периода.

При описании дискретных систем скорость изменения решетчатой функции будет характеризоваться ее разностью производных более высоких порядков, которые заменяются разностями соответствующего порядка.

Разность 1 порядка в некоторой точке n определяется так:

Разность 2 порядка определяется так:

ля k-го порядка:

Тогда дискретную систему можно описать конечно-разностными уравнениями, определяющими соотношение между выходной функцией y(n), ее разностью и входной функцией x(n) и ее разностями.

Решение конечно-разностного уравнения [1] можно представить в виде общего решения однородного уравнения и частного решения неоднородного уравнения.

.

Для решения этого уравнения необходимо задать начальные условия Линейные дискретные системы описываются с помощью линейного уравнения [1], а нелинейные с помощью нелинейного уравнения [1].