Частотная форма записи передаточной функции.

В передаточной функции в форме преобразований по Лапласу р является комплексной переменной. Ее вид . Пусть(комплексная переменная является чисто мнимой), тогда получим передаточную функцию в частотной форме:

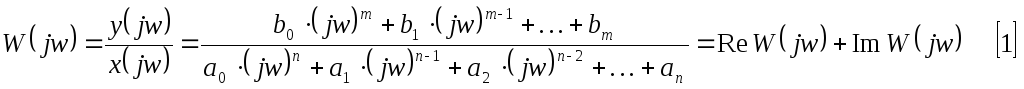
Частотную форму передаточной функции можно записать в показательной форме, и тогда она примет вид:

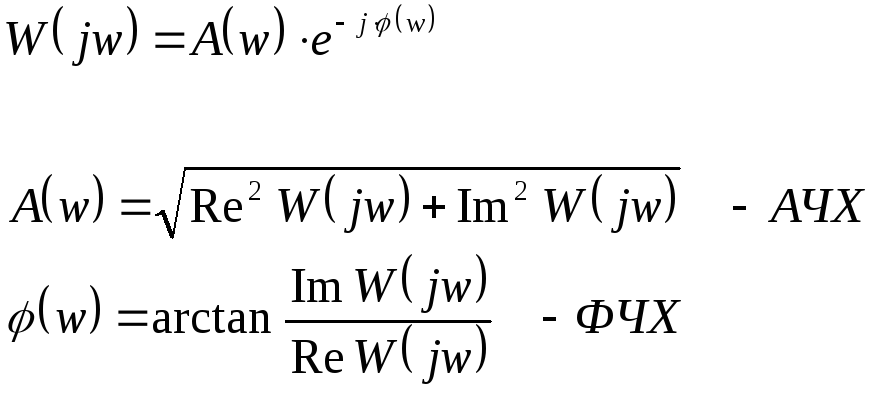
Вопросы для самоконтроля.

1. Математические модели динамических систем.

2. Линеаризация. Метод малых отклонений.

3. Линейные динамические системы.

4. Передаточные функции систем. Операторная форма.

5. Стандартная форма. Форма по Лапласу.

6. Свойства преобразований по Лапласу.

7. Частотная теорема передаточных функций.

Лекция 3. Входные воздействия

Цель. Изучить типовые входные воздействия на системы.

Задачи:

1. Изучить виды входных воздействий.

2. Изучить способы их нахождения.

Все входные воздействия можно разделить на детерминированные и стохастические.

Из всех входных детерминированных воздействий можно выделить типовые, к которым относятся:

1). Единичное ступенчатое воздействие: .

2). Импульсное воздействие: .

3). Гармоническое.

Функция времени, описывающая изменение выходных величин, которые вызваны каким-либо входным воздействием, называются откликами или реакцией системы на это входное воздействие.

1. Единичное ступенчатое воздействие – это воздействие вида:

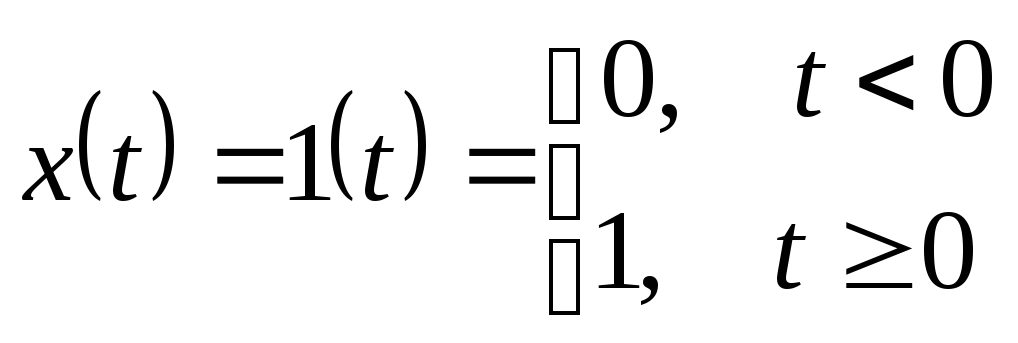
Функция, определяющая изменение выходной величины системы при подаче на ее вход единичного ступенчатого воздействия и при нулевых начальных условиях называется переходной функцией системы и обозначается: h(t).

Способы получения

1). Экспериментальный.

В этом случае на вход системы подается единичное ступенчатое воздействие и экспериментально определяется значение выходной функции. По полученным точкам строится график.

2). Аналитический.

В этом случае решается исходное дифференциальное уравнение.

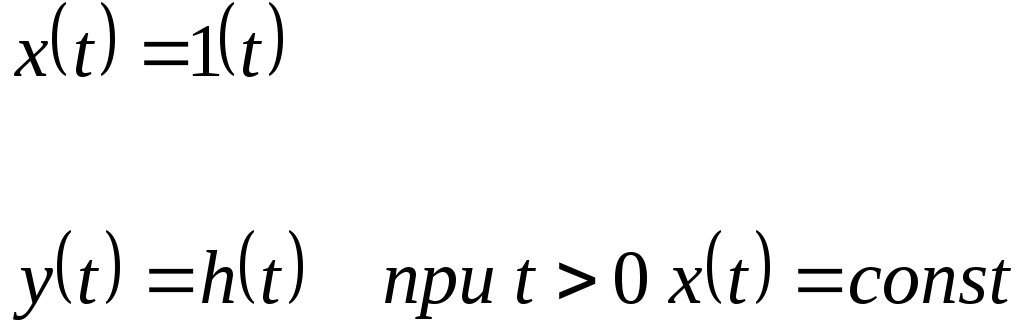
3). С помощью преобразований Лапласа.

Определим изображение 1(t).

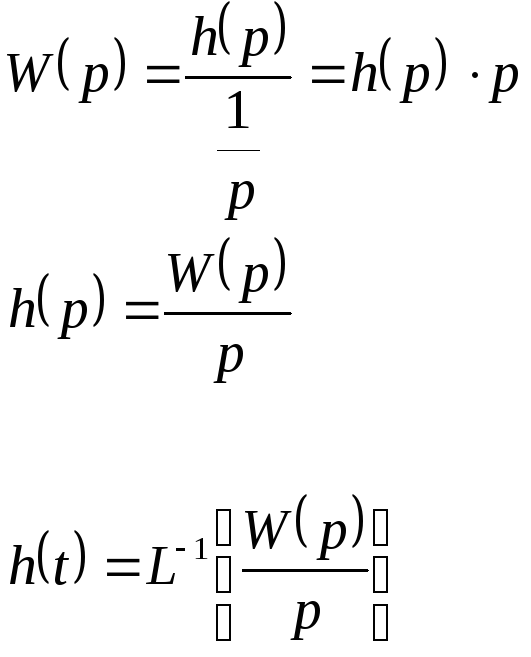
2. Импульсное воздействие.

- это воздействие вида:

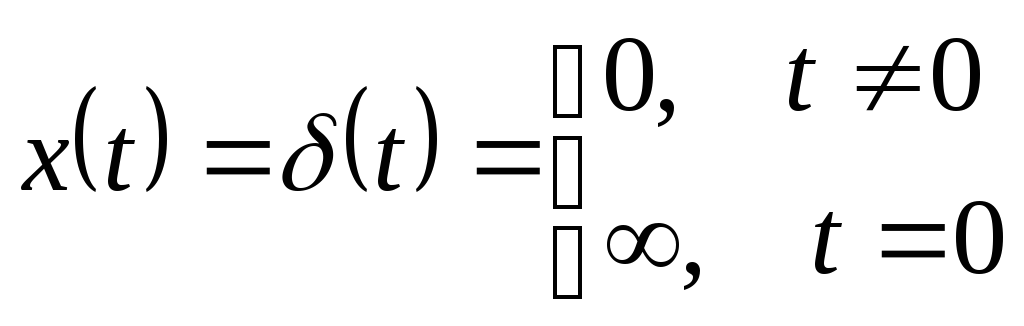
Функция, определяющая изменение выходной величины некоторой системы при подаче на ее вход единичного импульсного сигнала при нулевых начальных условиях называется импульсной переходной функцией системы и обозначается: w(t).

Рассмотрим геометрическую интерпретацию определения импульсного воздействия. Пусть в момент времени t=0 определяется единичным ступенчатым воздействием амплитуды k, а в момент времени, смещенный на величину Δt – ступенчатое воздействие с амплитудой – К.

Тогда выходной сигнал системы будет:

Уменьшая время Δt и увеличивая амплитуду импульса таким образом, что при Δt стремящемся к 0, получим:

Определим импульсную переходную функцию с помощью преобразований Лапласа.

.

Определим изображение весовой функции.

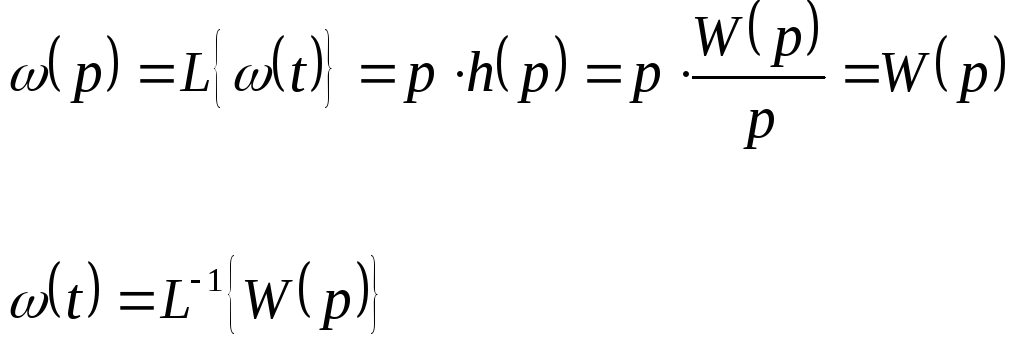
3. Гармоническое воздействие.

В отличие от временных характеристик , описывающих переходные процессы в системе, реакция на гармоническое воздействие описывает вынужденные установившееся колебания выходной величины. Гармоника входного воздействия – это воздействие вида:

- амплитуда, w-угловая частота. В этом случае реакция на гармоническое воздействие будет иметь вид:

Тогда:

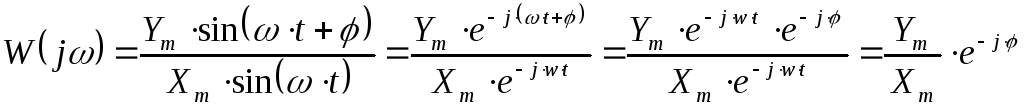
- амплитуда частотной формы передаточной функции.