Линейные динамические системы.

В общем, виде линейную динамическую систему можно описать с помощью дифференциального уравнения, определяющего связь между входной величиной x(t) и выходной y(t). Это уравнение будет иметь вид:

- постоянные величины, характеризующие параметры звена. Коэффициенты - константы, определяющие параметры входного сигнала.

Задавая различные выражения для входного сигнала по уравнению [7], можно определить выходной сигнал y(t), при этом должно быть задано n начальных условий.

Запишем уравнение установившегося состояния или статическую характеристику элемента. Определить все свойства исследуемого элемента и его переходный процесс можно, решив дифференциальное уравнение [7].

Методы решения.

1. Аналитический – в этом случае решение дифференциального уравнения ищется в общем виде.

2. Численный – в этом случае в общем виде решение не получают, а получают численное значение для заданных входных параметров.

3. Качественный – в этом случае решения уравнения не получают, а определяют некоторые требуемые его свойства.

При аналитическом методе решения уравнения, решение получают в виде:

,

где -представляет собой решение однородного дифференциального уравнения [8].

- частное решение неоднородного уравнения [7].

Общее решение однородного дифференциального уравнения [8] можно представить в виде:

где - некоторые коэффициенты, определяемые из начальных условий, а p_i – корни характеристического уравнения [9].

Частное решение уравнения [7] будет зависеть от свойств и вида входного сигнала.

Определить корни характеристического уравнения порядка выше 3 практически невозможно, поэтому для получения аналитических зависимостей выходного сигнала от входного используют операторные методы, основанные на преобразовании Лапласа. В этом случае используется понятие передаточной функции элемента или системы.

Передаточная функция системы.

Рассмотрим некоторый элемент или систему, на вход которой подали сигнал «x», а на выходе получили «y».

Передаточной функцией системы или элемента называют отношение выходной величины к входной при нулевых начальных условиях.

Передаточная функция может быть записана в 4 формах:

1. операторная.

2. стандартная.

3. в форме изображений по Лапласу.

4. частотная.

Операторная форма записи передаточной функции.

Введем в уравнение [7] оператор дифференцирования «р» , тогда [7] примет вид:

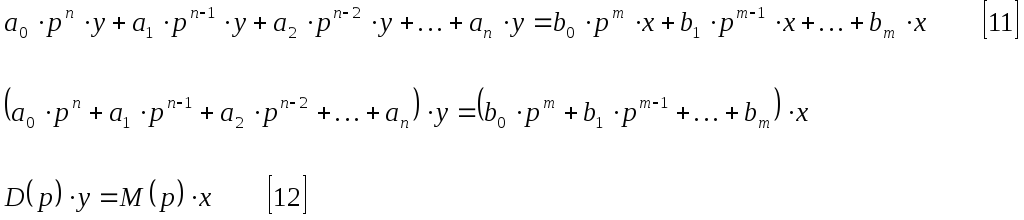
D(p) – характеристический многочлен, а - характеристическое уравнение.

Используя [12], определим передаточную функцию элемента:

Полученное выражение для передаточной функции называется операторной формой записи передаточной функции.

Стандартная форма записи передаточной функции.

Преобразуем [13] к виду:

это стандартная форма записи передаточной функции.

Величина называется коэффициентом передачи системы,

Величины

- постоянные времени. Тогда [14] примет вид:

Передаточная функция в форме изображений по Лапласу.

Для получения передаточной функции в форме изображений по Лапласу используют преобразования, приводящие функцию действительного аргумента t в функцию мнимого переменного р.

- преобразование Лапласа

Рассмотрим уравнение [7]. Преобразуем функцию y(t) по Лапласу.

Для правой части [7] можно получить, что:

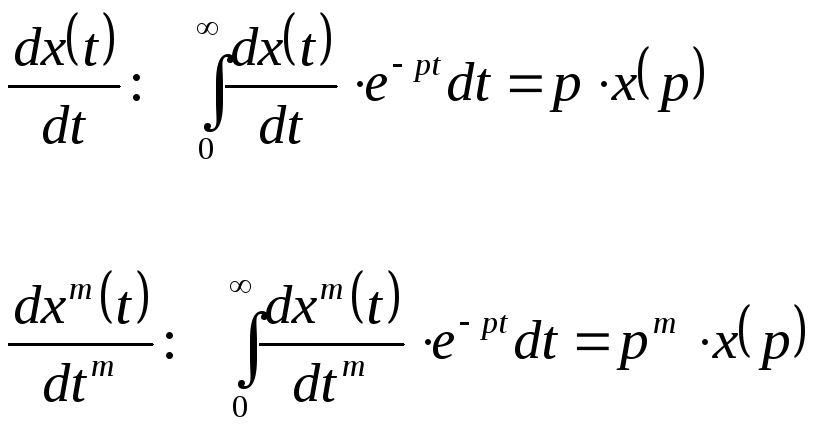
Подставляя в [7], получим:

обратное преобразование Лапласа преобразует функцию комплексного переменного р в функцию действительного переменного t.

Свойства:

1).

2). Если ,, то:

3).

4). если оригинал смещается на некоторую величину , причеми, то смещенная функция примет вид:

.

5). Если изображение смещается на р₀, то оно соответственно будет равно:.

6). Произведение 2 изображений равно:

7).

8). Свойство дифференцирования. Если иf(t) непрерывно дифференцируема, то производная порядка n будет равна:

9). Свойство интегрирования.