Свойства функции и плотности распределения вероятности многомерной случайной величины.

1. значения многомерной функции случайной величины находится на интервале

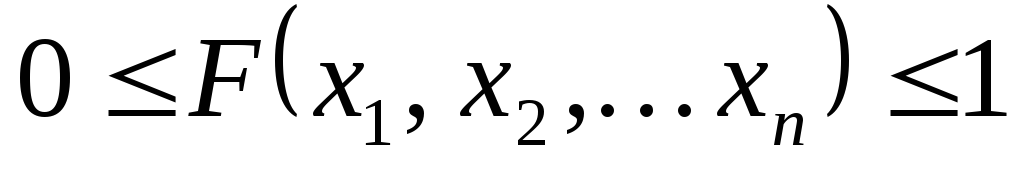
2. Функция распределения вероятностей многомерной случайной величины не убывает по любому из своих аргументов:

3. Если все аргументы функции распределения вероятностей равны , то значение функции распределения вероятностей равно =1.

4. Если хотя бы один из аргументов функции распределения вероятностей равен 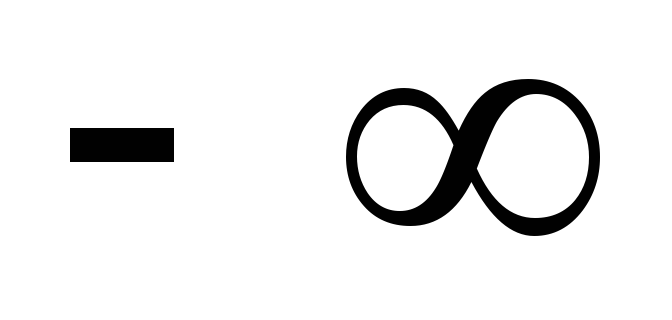, то значение функции распределения вероятностей равно =0.

5. Если k аргументов функции распределения вероятностей равны 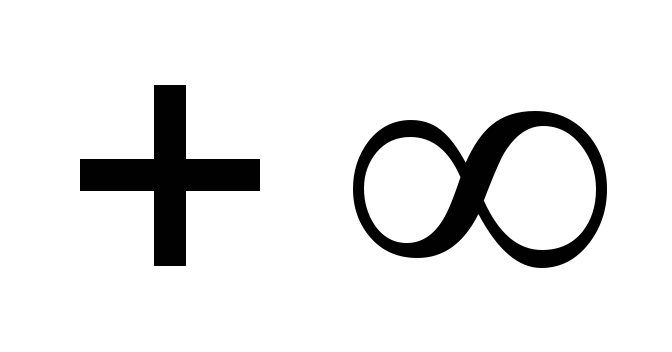, то порядок функции распределения вероятностей может быть снижен наk.

6. Вероятность того, что вектор 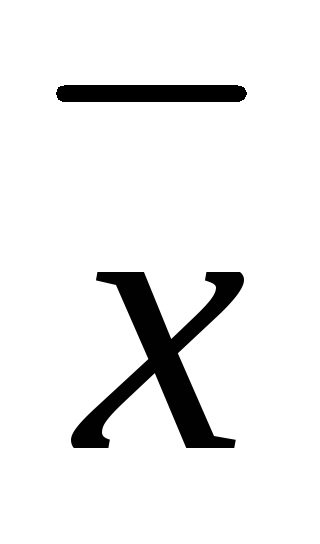принимает случайные значения из некоторой области А, равнаn-мерному интегралу.

7. Плотность распределения вероятностей многомерной случайной величины есть величина неотрицательная.

8. N мерный интеграл от функции распределения равен 1.

9. Функция распределения вероятностей n мерной случайной величины может быть определена как n мерный интеграл.

Числовые характеристики случайной величины.

Математическое ожидание или среднее значение.

Непрерывная случайная величина:

Дискретная случайная величина:

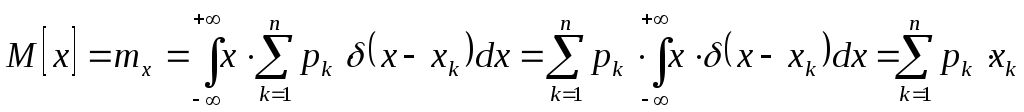
Пусть случайная величина «у» является неслучайной функцией φ случайного аргумента «х». Тогда:

в том случае, если «у» - дискретная случайная величина, то:

Дисперсия.

Дисперсия характеризует величину разброса случайных значений вокруг математического ожидания.

Непрерывная случайная величина:

Дискретная случайная величина:

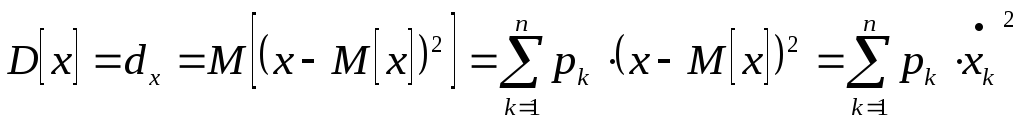
Корреляционная функция.

Корреляционная функция определяет связь между случайными функциями или случайными величинами.

Рассмотрим 2 случайных величины x_i и x_j.

Тогда корреляционная функция будет определяться так:

Свойства корреляционной функции:

1.

2.

3. Если случайные величины x_i и x_j независимы, то корреляционная функция равна 0.

В том случае, если корреляционная функция определяется для многомерной случайной величины, то она будет иметь вид матрицы:

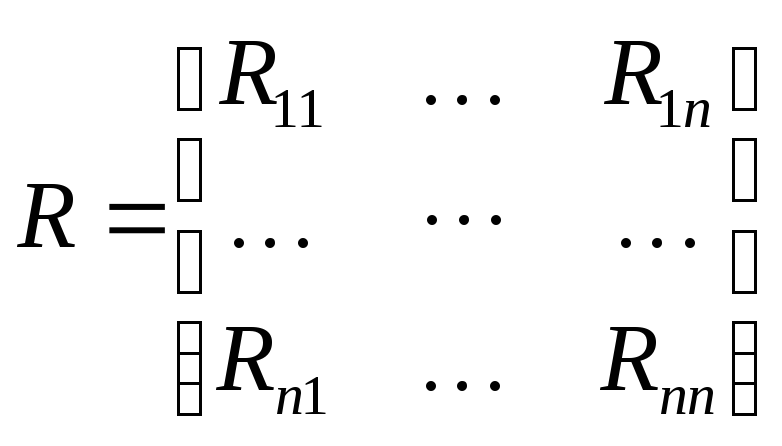
Эта матрица называется корреляционной матрицей.

Величина, определяемая как:

называется коэффициентом корреляции.

Свойства коэффициента корреляции:

1.

2.

3. .

4. Если величины x_i и x_j независимы, то коэффициент корреляции равен 0.

Числовые характеристики для случайных функций или процессов.

Рассмотрим некоторую непрерывную случайную функцию x(t).

Математическое ожидание случайной функции имеет вид:

Дисперсия случайного процесса – это величина, определяемая как:

Корреляционная функция случайного процесса:

Взаимная корреляционная функция определяется:

Корреляционная функция некоторого случайного процесса характеризует взаимосвязь значений случайных функций в моменты времени .

Взаимная корреляционная функция характеризует взаимосвязь между случайными функциями или процессами Х и У в моменты времени .

Вопросы для самоконтроля.

1. Плотность и функция распределения вероятности для непрерывных случайных величин.

2. Плотность и функция распределения вероятности для многомерных и дискретных случайных величин.

3. Свойства функции плотности распределения.

4. Числовые характеристики случайных величин.

5. Числовые характеристики случайных процессов.