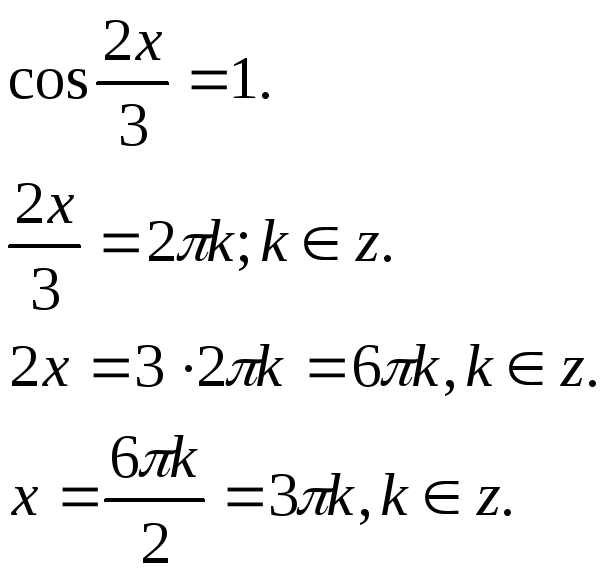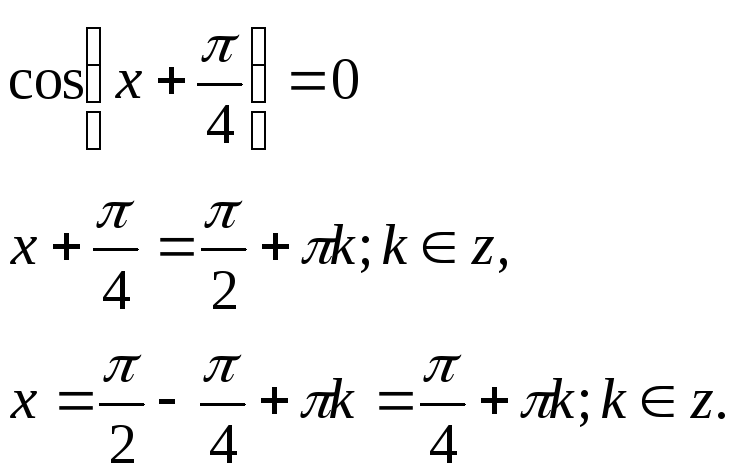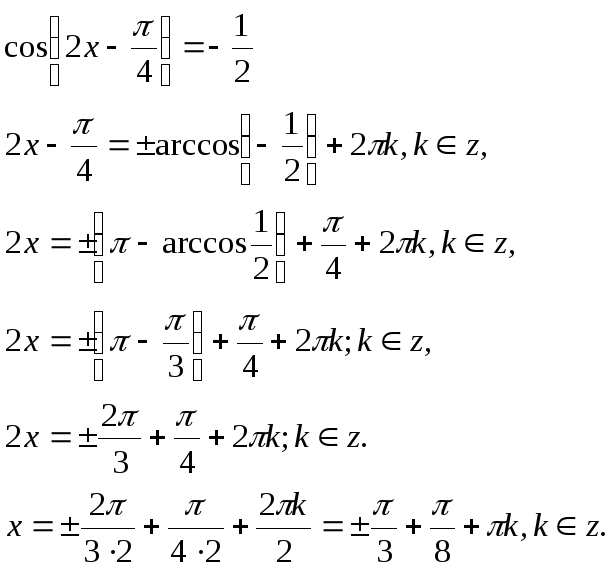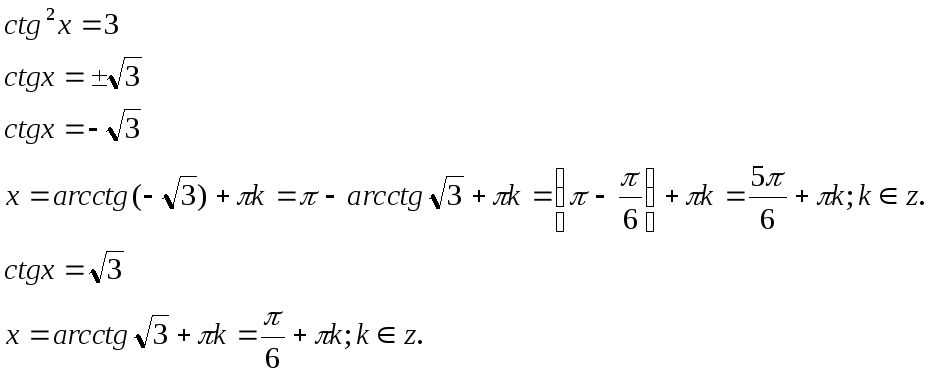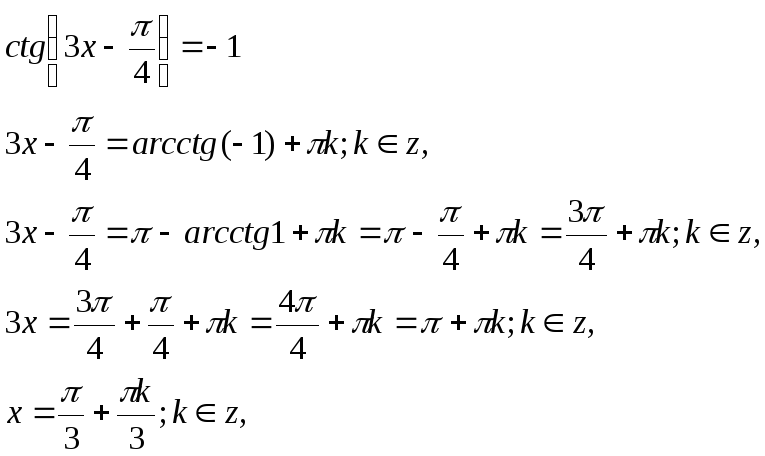Розв’язання тригонометричних рівнянь

Розв’яжіть рівняння:

1. 

Відповідь:

2. 

Відповідь:

3. 

Відповідь:

4. 

Відповідь: .

5. 

Відповідь:

6. 

Відповідь:

7. 

Відповідь:

8. 

Відповідь:

9. 

Відповідь:

10. 

Відповідь:

11. 

Відповідь:

12. 

Відповідь:

13. 

Відповідь:

14. 

Відповідь: ,.

15. 

Відповідь: ,

16. 

Відповідь; ,

17. 

Відповідь:

18. 

Відповідь: ;

19. 

Відповідь:

20. 

Відповідь:

21. 

Відповідь:

Лекція № 11 Гармонічні коливання План вивчення теми

1. Приклади фізичних процесів, які називаються гармонічними коливаннями (коливання струни, маятник, напруга в колі змінного струму тощо).

2. Функції, що описують гармонічні коливання: .

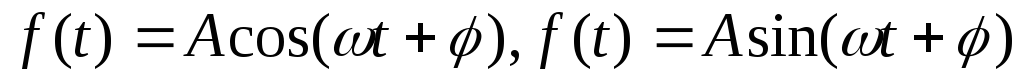3. Параметри , що визначають гармонічні коливання: амплітуда, кутова частота, початкова фаза, період гармонічного коливання.

Домашнє завдання: конспект;[3]c.164-170.

Гармонічні коливання – це процес, який можна описати функцією вигляду . Будь – яка величина здійснює гармонічні коливання, якщо з плином часу вона змінюється за законом .

Гармонічне коливання є найпростішою математичною моделлю, що описує коливальні процеси у природі і техніці. За законом гармонічного коливання відбувається рух вантажу, прикріпленого до ідеальної пружини, за умови, що опором повітрям можна знехтувати. Справді, якщо на прямій, вздовж якої рухається вантаж (точка Р), ввести координату х так, щоб у положенні рівноваги (хР=0) відтягнути вантаж у додатному напрямку на відстань А і в момент часу t=0 відпустити його, то залежність координати точки Р від часу t=o (мал. 1) матиме такий вигляд: , - коефіцієнт пружності.

Цей закон добре описує електромагнітні коливання у радіотехніці, коливання кожної точки натягнутої струни, яку виведено з положення рівноваги, коливання молекул середовища, в якому поширюється звук.

Гармонічне коливання визначається трьома параметрами: амплітудою , кутовою швидкістю і початковою фазою .Аргумент називається фазою. Обернена величина називається частотою коливання.

Коливання доводиться додавати. У механіці це зумовлено тим, що на точку може діяти кілька сил, кожна з яких викликає гармонічні коливання. Додавання гармонічних коливань відбувається при вмиканні в одну мережу генераторів змінного струму, при поширенні звуку від двох близько розміщених джерел звуку. При додаванні гармонічних коливань однієї і тієї самої частоти дістаємо знову гармонічне коливання тієї самої частоти. Це означає , що сума двох функцій і і є функцією того самого вигляду: .

Приклад. Знайти суму гармонічних коливань .

Тут

Амплітуда суми коливань дорівнює 4, а початкова фаза .