
- •Тригонометричні функції План
- •Література:
- •Тригонометричні функції кутів
- •Тригонометричні функції числових аргументів.
- •Лекція № 3 Формули зведення. Перетворення виразів. (Самостійна робота. Тригонометричні функції суми та різниці двох кутів, подвійного аргументу.) План вивчення теми
- •Формули додавання.
- •Формули подвійних кутів.
- •Лекція № 4 Перетворення суми і різниці тригонометричних функцій на добуток. Перетворення добутку тригонометричних функцій в суму. План вивчення теми
- •Лекція № 5 Тригонометричні функції, їх графіки та властивості
- •Властивості і графіки синуса і косинуса.
- •Функція додатна на кожному з інтервалів , від’ємна на кожному з інтервалів
- •Функція зростає на кожному з проміжків і спадає на кожному з проміжків
- •Найбільшого значення, що дорівнює функція набував при і найменшого значення, яке дорівнює при
- •Лекція № 7 Оберненні тригонометричні функції. План вивчення теми
- •Лекція № 8 – 10 Розв’язування найпростіших тригонометричних рівнянь та нерівностей. План вивчення теми
- •Розв’язання тригонометричних рівнянь
- •Лекція № 11 Гармонічні коливання План вивчення теми
Властивості і графіки синуса і косинуса.
Дослідження
реальних процесів, які моделюються за
допомогою тригонометричних функцій,
зводиться до вивчення властивостей
функцій
![]() ,
,
![]()


Властивості:
![]() ,
,
![]()
-
Функції
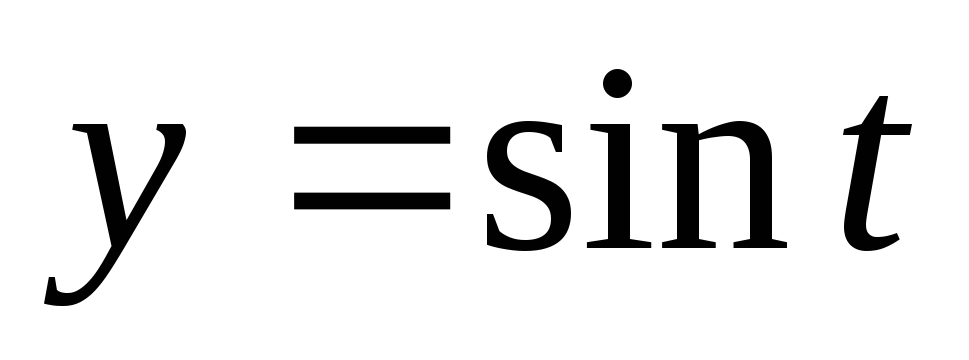 ,
,
 визначені
на всій числовій осі.
визначені
на всій числовій осі.
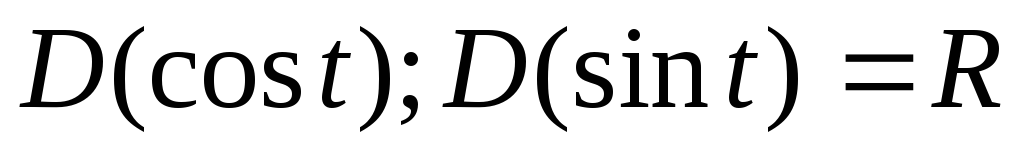
- кожному
дійсному числу
![]() поставлена у відповідальність точка
поставлена у відповідальність точка
![]() одиничного кола, а тому і її абсциса та
ордината, тобто косинус і синус числа
одиничного кола, а тому і її абсциса та
ордината, тобто косинус і синус числа
![]()
2)
Множиною
значень функцій
![]() ,
,
![]() є
відрізок
є
відрізок
![]()
![]()
![]()
![]()
![]()
Всі
значення косинуса і синуса містяться
між
![]() і
і
![]() .
Оскільки при непереривному переміщенні
точки
.
Оскільки при непереривному переміщенні
точки
![]() по одиничному колу її проекції на осі
по одиничному колу її проекції на осі
![]() та
та
![]() неперервне переміщуються вздовж
вертикального та горизонтального
діаметрів, функції
неперервне переміщуються вздовж
вертикального та горизонтального
діаметрів, функції
![]() ,
,
![]() набуватимуть всіх значень з відрізка
набуватимуть всіх значень з відрізка
![]() .
.
-
Функція
 непарна, а функція
непарна, а функція
 парна,
тобто для кожного
парна,
тобто для кожного
![]()
![]()
Графік
непарної функції
![]() симетричний
відносно початку
координат, графік парної функції
симетричний
відносно початку
координат, графік парної функції
![]() симетричний
відносно осі ординат.
симетричний
відносно осі ординат.
4)
Функції![]() ,
,
![]() -
періодичні,
з
найменшим додатним періодом
-
періодичні,
з
найменшим додатним періодом
![]()
Функція
![]() називається періодичною,
якщо існує таке число
називається періодичною,
якщо існує таке число
![]() ,
що область визначення функції разом із
коленою точкою
,
що область визначення функції разом із
коленою точкою
![]() містить точки
містить точки
![]() і при цьому виконується рівність
і при цьому виконується рівність
![]() Число
Число
![]() називається періодом функції.
називається періодом функції.
![]() -
найменший додатний період косинуса,
синуса.
-
найменший додатний період косинуса,
синуса.
-
Нулі функції
 ,
,
 це точки перетину осі
це точки перетину осі

![]()
![]()
![]()
![]()
-
Функція додатна на кожному з інтервалів , від’ємна на кожному з інтервалів
Функція
![]() додатна
на кожному
з проміжку
додатна
на кожному
з проміжку
![]() і від’ємна на кожному з проміжків
і від’ємна на кожному з проміжків
![]()
-
Функція зростає на кожному з проміжків і спадає на кожному з проміжків
Функція
![]() зростає
на
кожному з проміжків
зростає
на
кожному з проміжків
![]()
![]() і спадає на кожному з проміжків
і спадає на кожному з проміжків
![]()
![]()
-
Найбільшого значення, що дорівнює функція набував при і найменшого значення, яке дорівнює при
Функція
![]() набуває найбільшого
значення , що дорівнює
набуває найбільшого
значення , що дорівнює
![]() при
при
![]()
![]() і найменшого значення , що дорівнює
і найменшого значення , що дорівнює
![]() при
при
![]()
![]()
![]()
![]() .
.
9)
Функції
![]() ,
,
![]() неперервні на всій числовій осі.
неперервні на всій числовій осі.
![]()
Лекція № 6 Побудова графіків тригонометричних функцій. Перетворення графіків тригонометричних функцій.
План вивчення теми
-
Графік функції
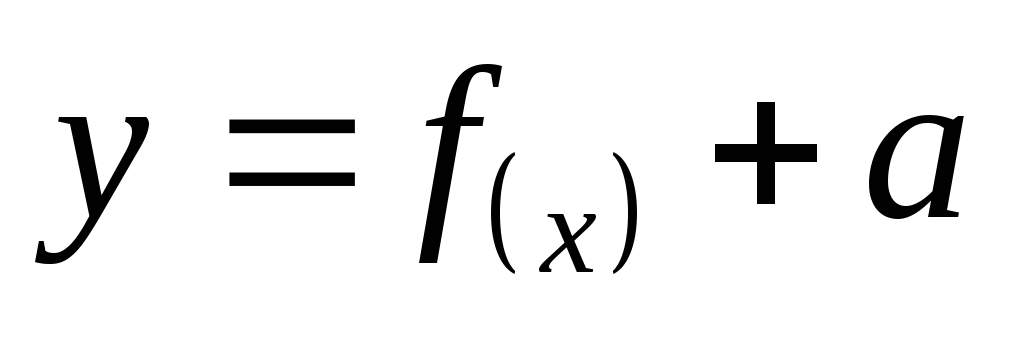 .
.
-
Графік функції
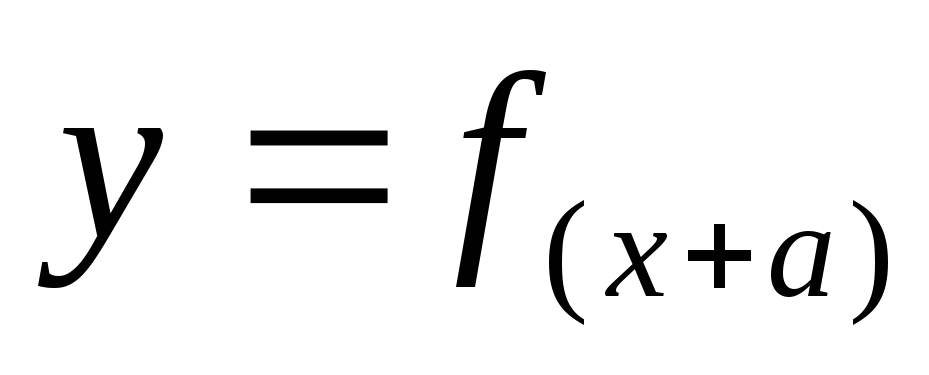 .
. -
Графік функції
 та
інші графіки.
та
інші графіки. -
Приклади.
Домашнє завдання: [3]гл.3§1-3 с.164-170, [4] p1 §5,6; опорний конспект.
А як
побудувати, наприклад, графіки функцій
![]() ,
,
![]()
![]() ?
?
1.Для
побудови графіка функції
![]() треба графік функції
треба графік функції
![]() перенести вздовж вісі Оу на
перенести вздовж вісі Оу на
![]() одиниць вверх, якщо
одиниць вверх, якщо
![]() ,
та на
,
та на
![]() одиниць вниз, якщо
одиниць вниз, якщо
![]() .
.

 2.
Для побудови графіка функції
2.
Для побудови графіка функції
![]() необхідно
графік функції
необхідно
графік функції
![]() перенести вздовж вісі Ох на
перенести вздовж вісі Ох на
![]() одиниць вправо коли
одиниць вправо коли
![]() ,
та на
,
та на
![]() одиниць вліво коли
одиниць вліво коли
![]() Побудуємо
Побудуємо
![]()
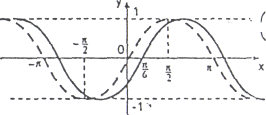
3. Для
побудови графіка функції
![]() необхідно графік функції
необхідно графік функції
![]() відобразити симетрично відносно вісі
Ох.
відобразити симетрично відносно вісі
Ох.
Побудуємо
![]()
4. Для
побудови графіка функції
![]() необхідно графік функції
необхідно графік функції
![]() відобразити симетрично відносно вісі
Оу.
відобразити симетрично відносно вісі
Оу.
Побудуємо
![]() .
.

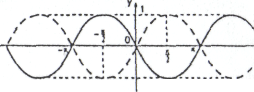
5. Для
побудови графіка функції
![]() необхідно додатну частину графіка
необхідно додатну частину графіка
![]() лишити незмінною , а від’ємну частину
відобразити симетрично вісі Ох.
лишити незмінною , а від’ємну частину
відобразити симетрично вісі Ох.
Побудуємо
![]() .
.

-
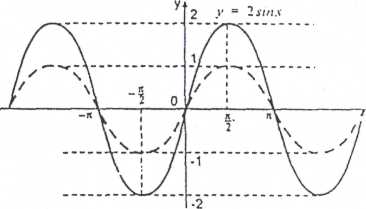
Для побудови графіка необхідно ординати усіх точок графіка
необхідно ординати усіх точок графіка
 помножити на
помножити на
 ,
лишив при цьому незмінними абсциси.
Якщо
,
лишив при цьому незмінними абсциси.
Якщо
 графік
графік
 получається з графіка
получається з графіка
 розтягненням його від вісі Ох у
розтягненням його від вісі Ох у
 раз, а при
раз, а при
 -
стисканням до вісі Ох в
-
стисканням до вісі Ох в
 раз. Деформації графіка
раз. Деформації графіка
 виконується в перпендикулярному напрямі
до вісі Ох.
виконується в перпендикулярному напрямі
до вісі Ох.



![]() ,
треба графік функції
,
треба графік функції
![]() «розтягнути» від осі
«розтягнути» від осі
![]() у 3 рази. Чому?
у 3 рази. Чому?


![]()

7. Для
побудови графіка
![]() необхідно абсциси усіх точок графіка
необхідно абсциси усіх точок графіка
![]() поділити на
поділити на
![]() ,
лишив ординати незмінними. Якщо
,
лишив ординати незмінними. Якщо
![]() ,то
графік
,то
графік
![]() получається з графіка
получається з графіка
![]() стисканням його до вісі Оу в
стисканням його до вісі Оу в
![]() раз,
а при
раз,
а при
![]() розтяганням графіка
розтяганням графіка
![]() від вісі Оу в
від вісі Оу в
![]() раз. Деформації графіка
раз. Деформації графіка
![]() виконується в перпендикулярному напрямі
до вісі Оу.
виконується в перпендикулярному напрямі
до вісі Оу.

Щоб
побудувати графік функції
![]() ,
треба графік функції
,
треба графік функції
![]() «стиснути» від осі
«стиснути» від осі
![]() вдвічі. Чому?
вдвічі. Чому?

Щоб
побудувати графік функції
![]() ,
треба графік функції
,
треба графік функції
![]() перенести на 2 одиниці вліво.
перенести на 2 одиниці вліво.

Так само можна перетворювати й інші графіки тригонометричних функцій.
