Правило Крамара:

Если определитель матрицы коэффициентов системы с одинаковым количеством уравнений и неизвестных не равен нулю, то эта система имеет единственное решение, которое может быть найдено с помощью определителей по формуле: где – матрица, получаемая путём замены i ого столбца на столбец свободных членов.

Доказательство:

Если количество неизвестных не равно количеству уравнений, или определитель матрицы коэффициентов равен нулю, то правило Крамара не применяется.

Вопрос № 7: Линейная зависимость и независимость строк и столбцов матрицы:

1. Линейная зависимость и независимость строк и столбцов матрицы.

   1. Определение.

   2. Свойства.

2. Общее условие равенства нулю определителя.

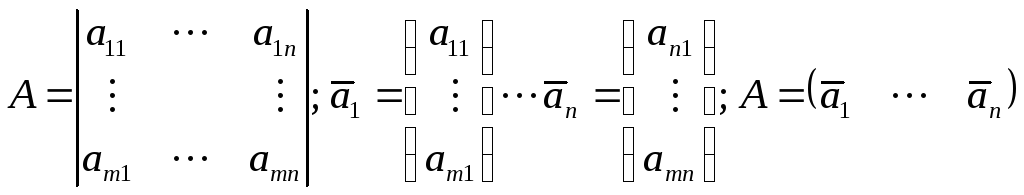
– линейная комбинация столбцов того же порядка, если его можно представить в виде взвешенной суммы. – коэффициент линейных комбинаций, или весовой коэффициент.

Пусть

Система и п столбцов одного и того же порядка называется линейно зависимой, если существуют такие , что линейная комбинация равна , следовательно хотя бы один из этих столбцов является , либо может быть выражен в виде линейной комбинации других столбцов.

Система из п столбцов является линейно независимой, если равенство их линейной комбинации возможно лишь в случае, когда все весовые коэффициенты – нули.

Свойства:

1. Дополнения к линейно зависимой системе любых других столбцов приводит к ассиметричной линейной зависимости.

2. Исключение из линейно-независимой системы любых столбцов даёт независимую подсистему.

Необходимое и достаточное условие равенства нулю определителя матрицы:

Для того чтобы определитель матрицы был равен нулю необходимо и достаточно чтобы хотя бы один из его столбцов или строк был линейной комбинацией остальных, или чтобы столбцы, или строки были линейно зависимы.

Вопрос № 8: Миноры матриц:

1. Миноры матриц.

   1. Определение.

   2. Свойство.

2. Базисный минор.

   1. Теорема о базисном миноре матрицы.

3. Ранг матрицы.

   1. Теорема о ранге матрицы.

Минором матрицы порядка к называют определитель , составленный из элементов этой матрицы, стоящих на пересечении произвольным образом выбранных к-ых строк и к-ых столбцов этой матрицы.

Базисный минор:

Базисным минором матрицы А называется такой минор порядка r, который не равен нулю, а все миноры рангом выше равны, или не существуют.

Свойство:

Если в матрице все миноры М_к равны нулю, то все миноры высших порядков так же будут равны нулю, так как они вычисляются по элементам строк и столбцов, а значит выражаются через М_к.

Базисный минор – это минор номинального порядка, не равный нулю.

Произвольная матрица, каждый столбец, или строка которой является линейной комбинацией строк, или столбцов, входящих в базисный минор.

Рангом матрицы называется порядок её базисного минора.

Теорема о ранге.

Ранг матрицы соответствует количеству её линейно независимых строк, или столбцов.

Вопрос № 9: Вычисление ранга матрицы методом окаймляющих миноров:

Пусть в матрице найден минор порядка к, отличный от нуля, тогда достаточно рассмотреть лишь те миноры к+1 порядка, которые содержат внутри себя, то есть окаймляют минор к-ого порядка.

Если все они равны нулю, то минор к-ого порядка – базисный минор, а ранг матрицы равен рангу базисного минора, то есть матрица – к-ого порядка, ну а если существуют миноры, не равные нулю, ранг которых больше к, то операцию поиска необходимо продолжать. к:=л+1;

Пример:

М₂ – базисный минор, ранг матрицы равен двум.

Вопрос № 10: Вычисление ранга матриц методом элементарных преобразований:

Элементарные преобразования матрицы:

1. Перестановка строк, или столбцов матрицы.

2. Умножение строки, или столбцы на число, отличное от нуля.

3. Сложение строк (столбцов) матрицы.

Теорема об элементарных преобразованиях матрицы:

При элементарных преобразованиях ранг матрицы не изменяется, поэтом при помощи элементарных преобразований матрица приводится к ступенчатому, или блочно треугольному виду, по которому ранг можно определить визуально.

Пример:

Правило определения ранга матрицы и её базисного минора:

1. Ранг ступенчатой матрицы равен количеству её не нулевых строк.

2. Базисный минор ступенчатой матрицы содержится среди элементов её не нулевых строк и такого же количества её столбцов, взятых по одному из каждой ступеньки.

Вопрос № 11: Теорема Кронекера-Капели:

1. Теорема Кронекера-Капели.

2. Общий метод решения систем из т алгебраических уравнений с п неизвестными.

Условие совместности

Рассмотрим произвольную систему из т уравнений с п неизвестными: , тогда ,

Теорема Кронекера-Капели:

Система совместна, если ранг расширенной матрицы равен рангу матрицы коэффициентов.

Доказательство:

Необходимое условие:

Если система совместна, то ранг расширенной матрицы и ранг матрицы коэффициентов равны.

Следовательно, столбец свободных членов линейно зависит от столбцов матрицы коэффициентов, поэтом столбцы расширенной матрицы содержат тоже количество независимых столбцов, что и матрица коэффициентов, тогда добавление линейно зависимого столбца не изменит ранг матрицы. Следовательно, по теореме о ранге матрицы, ранг матрицы коэффициентов равен рангу расширенной матрицы.