3.2. Матричные операции и функции

Матричные операции – основа системы MATLAB:

1. Сложение матриц. Если и - матрицы одинаковых размеров, то их суммой называют матрицу того же размера , элементы которой .

2. Умножение матрицы на скаляр. Произведением матрицы на скаляр  называют матрицу , элементы которой .

3. Умножение матрицы , имеющей размер , на матрицу , имеющую размер , означает нахождение третьей матрицы размеров , причем элементы этой матрицы . Согласно определению данной операции, это правило действует, если число столбцов матрицы А равно числу строк матрицы В.

Определителем квадратной матрицы порядка n называют число (в MATLAB – det(A))

,

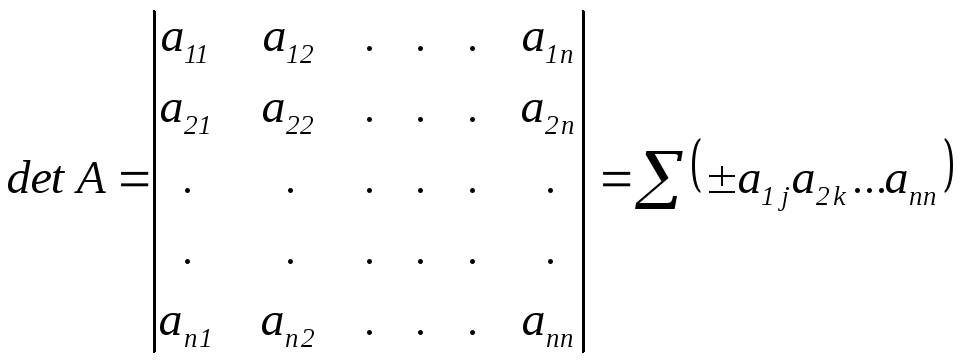где знак определяется числом (четным или нечетным) перестановок чисел . Способы вычисления определителей можно найти в соответствующей литературе. Квадратная матрица называется неособенной или невырожденной, если ее определитель (в противном случае матрица особенная, или вырожденная). Матрица называется обратной квадратной матрице А, если ; обратная матрица вычисляется довольно сложным образом:

,

где – алгебраические дополнения элементов матрицы.

Матрица называется транспонированной по отношению к матрице А, если в последней поменять местами столбцы и строки.

Транспонирование матрицы А:

» A=[1 2 3;4 5 6]

A =

1 2 3

4 5 6

» B=A'

B =

1 4

2 5

3 6

» [atan(1)*4 sin(pi/2) exp(1)]'

ans =

3.1416

1.0000

2.7183

Последний прием удобен при создании векторов-столбцов.

Сложение и вычитание матриц:

» A=[3 4 2;2 5 5]; B=[0 3 1; 3 7 8]; C=A+B, D=A-B

C =

3 7 3

5 12 13

D =

3 1 1

-1 -2 -3

Умножение матриц:

» A=[1:3;4:6], B=[7:9;10:12]', C=A*B

A =

1 2 3

4 5 6

B =

7 10

8 11

9 12

C =

50 68

122 167

Следует отметить такую важную операцию, как ; при этом матрица А превращается в пустую (и освобождает память), но сохраняется как объект; в то же время clear('А') уничтожает матрицу А как переменную MATLAB.

3.3. Решение линейных уравнений

Пусть задана система из трех линейных уравнений

.

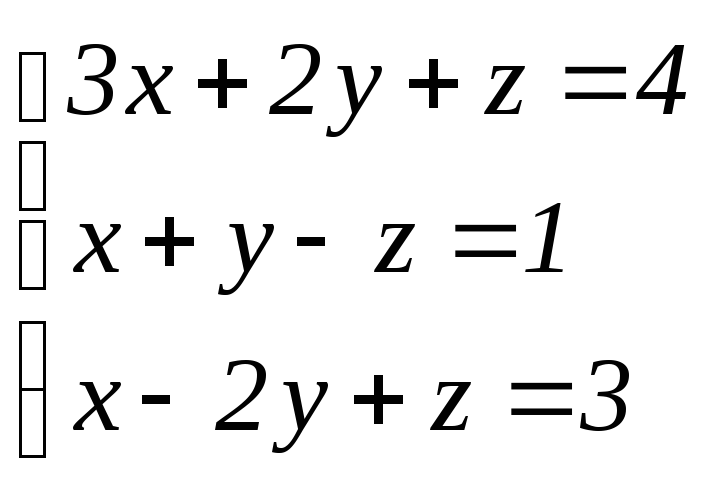Введем матрицу, составленную из коэффициентов левых частей уравнений:

.

Если рассматривать x, y и z как элементы матрицы-столбца , т.е. , а правые части системы как матрицу-столбец , то можно записать матричное уравнение . Умножая обе части этого ура­вне­ния на обратную матрицу , получим . Это соотношение за­писано на основании того, что – единичная матрица (с единичными эле­ментами на главной диагонали), а .

Команда для решения системы уравнений имеет вид

» A=[3 2 1;1 1 -1;1 -2 1]; B=[4 1 3]'; X=inv(A)*B, det(A)

X =

1.7000

-0.6000

0.1000

ans =

-10

Таким образом, ; существование решения подтверждается и тем, что определитель матрицы . Аналогичный результат получается при «левом» делении:

» A\B

ans =

1.7000

-0.6000

0.1000

Рекомендуется сравнить вычисление определителя матрицы вручную и с помощью системы MATLAB, например

» A=[1:3;4:6;7:9]; det(A)

ans =

0