7.1. Рабочая среда Simulink

Запуск Simulink осуществляется из командного окна MATLAB c помощью одного из трех способов:

1) по команде » simulink;

2) с помощью главного меню File-New-Model;

3) с использованием панели инструментов.

В результате открываются два окна: «библиотечное» (Library: simulink) и ра­бочее, в котором и организуется моделирование динамических систем (до сохранения файла ок­но остается безымянным – untitled).

В «библиотечном» окне находятся пиктограммы библиотек блоков, используемых при со­з­дании структурных схем динамических систем:

Sources – генераторы сигналов;

Sinks – анализаторы сигналов;

Discrete – дискретные блоки;

Linear – линейные блоки;

Nonlinear – нелинейные блоки;

Connections – типы соединений блоков;

Blocksets & Toolboxes – дополнительные блоки (в том числе пользовательские) и пакеты;

Demos – демонстрационные программы MATLAB и Simulink.

Библиотеки активизируют путем двойного щелчка левой клавишей мыши, в результате открываются окна, содержащие пиктограммы блоков соответствующего типа. Все окна Simulink имеют одинаковую структуру меню, но полностью его позиции обычно реализуются именно в рабочем окне. Большинство опций меню интуитивно понят­но, и поэтому в данном учебном пособии они подробно не рассматриваются. То же от­но­сится и к панели инструментов.

7.2. Представление динамической системы в виде струк­тур­ной схемы

Поведение динамической системы описывают с помощью некоторого оператора W, определяющего алгоритм преобразования входного воздей­ствия (сигнала) Y(t) в отклик (реакцию) X(t), т.е. .

В качестве оператора может выступать любая характеристика системы, функ­ци­о­наль­но связывающая воздействие и отклик, чаще всего – ДУ (или система ДУ) того или иного типа или передаточная функция (если система линейна). Сложную динамическую систему можно пред­ста­вить в виде совокупности некоторых типовых блоков (звеньев), соответствующим образом соединенных между собой. При этом получается структур­ная схема, которая и является моделью динамической системы. Идея о возможности рас­чле­нения динамической системы на отдельные функционально определенные блоки и ле­жит в основе программы Simulink.

В качестве примера рассмотрим известное уравнение линейной колебательной системы (осциллятора) , которое должно быть решено при начальных условиях: . Введем обозначения: . Тогда исходное уравнение можно представить в виде системы из двух ДУ первого порядка:

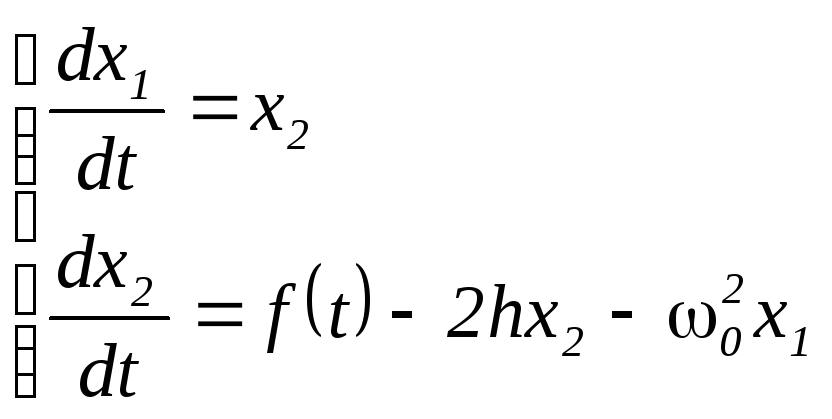, или .

Отсюда видно, что решение исходного ДУ, т.е. нахождение x и, в структурном смысле сводится к использованию двух последовательно соединенных интеграторов, на вход которых подаются соответствующие сигналы. Так получается в результате прямого интегрирования (с учетом начального значения) сигнала , поступающего с выхода предыдущего интегратора. Входной же сигнал последнего состоит из воздействия , формируемого с помощью задающего устройства (генератора), а также двух компонент, пропорциональных и . Таким образом, в структурной схеме модели должны быть предусмотрены две цепи обратной связи с соответствующими усилительными звеньями. Точно так же можно составить структурную схему S-модели для решения нелинейного ДУ; при этом, очевидно, потребуются блоки, реализующие нелинейные функциональные преобразования (см. разд. 5.4.3).

Если применить к исходному ДУ интегральное преобразование Лапласа, то можно получить передаточную функцию рассматриваемой системы, а именно (при нулевых начальных условиях):

.

В этом случае структурная схема будет состоять из одного (колебательного) звена, на вход которого необходимо подать воздействие . При ненулевых начальных условиях необходимо использовать соответствующие соотношения из операторного исчисления.