2.1.4. Усадка стружки и относительный сдвиг

Согласно современным представлениям, при образовании непрерывной и сплошной (сливной) стружки зона деформации имеет сложную форму и условно может быть разбита на несколько зон (рис. 2.11).

Рис. 2.11. Схема зоны деформации: A – зона стружкообразования с параллельными границами; Б – застойная зона адиабатических

деформаций, поперечное сечение «уса»; В и Г – зоны контактных

деформаций на передней и задней поверхностях

Однако более широко применяется упрощенная схема зоны деформации с единственной плоскостью сдвига, предложенная русским ученым – проф. И.А. Тиме [1].

Условие непрерывности (сплошности) несжимаемой деформируемой среды при образовании сливной стружки при плоской деформации выражается в постоянстве скорости в направлении 1–1 (рис. 2.1.8, б), перпендикулярном условной плоскости сдвига.

Для выполнения условий непрерывности несжимаемой среды при плоской деформации проекции скорости резания v (а при косоугольном резании – ее нормальной к режущей кромке составляющей в плоскости резания) и скорости стружки v₁ на нормаль к условной плоскости сдвига должны быть равны друг другу:

  или  . (2.21)

Из формулы (2.15) следует

. (2.22)

Рис. 2.12. Соотношения между скоростями стружки и детали

при деформации по схеме И.А. Тиме – единственной плоскости сдвига: а – схема зоны стружкообразования; б – план скоростей

Отношение скорости резания v к скорости стружки v_1, согласно терминологии, введенной И.А. Тиме [1], называют усадкой стружки  (а иногда – коэффициентом усадки стружки К).

Вследствие постоянства объема и равенства ширины стружки ширине срезаемого слоя усадка стружки может быть определена как отношение толщины стружки а₁ к максимальной толщине срезаемого слоя а_м [1]:

_. (2.23)

По усадке стружки  и переднему углу  вычисляется угол _у наклона условной плоскости сдвига, а также длина контакта С_А стружки с передней поверхностью режущего лезвия:

. (2.24)

Длина контакта С_А может быть оценена по формуле Н.Г. Абуладзе [1]

. (2.25)

Условие контакта инструмента со стружкой определяет величину скорости v₂, с которой стружка перемещается вдоль условной плоскости сдвига. Для большей наглядности рассмотрим соотношения между этими скоростями при неподвижной детали (например, при строгании) (рис. 2.13). Условие контакта стружки с инструментом требует, чтобы проекции скоростей стружки и резца на нормаль к передней поверхности режущего лезвия были равны друг другу, т. е. [1]

, откуда . (2.26)

Скорость v₂ характеризует перемещение частиц стружки, находящихся на верхней границе зоны стружкообразования относительно нижней в направлении условной плоскости сдвига.

Отношение скорости v₂, полученной из условия контакта стружки с резцом, к нормальной относительно условной плоскости сдвига составляющей скорости резания v_n = v sin_y называют относительным сдвигом  [ 1]:

(2.27)

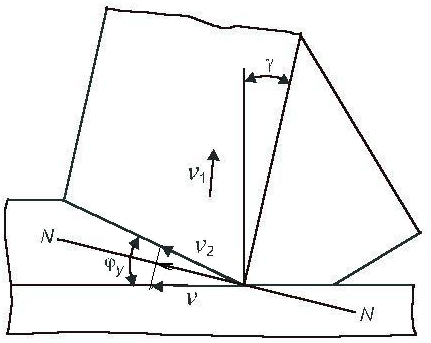
Рис. 2.13. Схема скоростей резца и стружки при строгании

Выражение для относительного сдвига в виде формулы (2.20) использовалось еще И.А. Тиме [1]. В специальной литературе используются и другие выражения для относительного сдвига , тождественные (2.20):

(2.28)

Термин «относительный сдвиг» заимствован из линейного преобразования, называемого простым сдвигом. Простой сдвиг является плоской однородной деформацией. Он может быть представлен в виде линейного преобразования вектора X=(x,y) в вектор X'=(x',y') (рис. 2.14):

(2.29)

Здесь  – тангенс угла , на который при простом сдвиге вдоль оси х повернулась сторона квадрата, перпендикулярная направлению сдвига, при преобразовании квадрата в параллелограмм, – относительный сдвиг:

(2.30)

где Ux – приращение перемещения вдоль оси x, y – высота деформируемого элемента в направлении оси y. При простом сдвиге относительный сдвиг  используется в качестве характеристики деформации.

Рис. 2.14. Однородная плоская деформация по схеме простого сдвига

Для пояснения правомерности применения схемы простого сдвига к резанию рассмотрим преобразование квадрата 1–2–3–4 в параллелограмм 1–2–3–4 при переходе его через зону стружкообразования в виде единственной плоскости сдвига (рис. 2.15).

Применительно к резанию, воспользовавшись ранее принятыми обозначениями, запишем: ,   , 

(2.31)

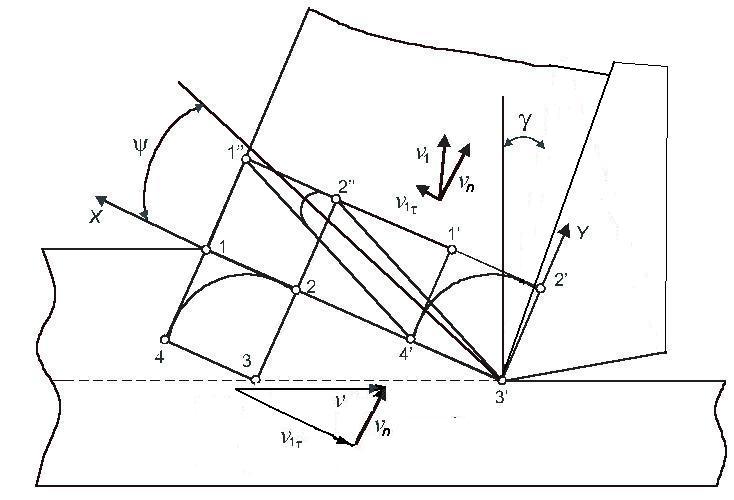
Рис.2.15. Преобразование квадрата 1–2–3–4 в параллелограмм

1–2–3–4 по схеме простого сдвига при прохождении его через зону стружкообразования

Относительный сдвиг часто называют характеристикой деформации при резании. Однако это было бы корректно, если бы деформация в зоне стружкообразования была однородной не только в стружке за конечной границей зоны стружкообразования, но и внутри этой зоны. В действительности деформация в зоне стружкообразования и в контактной пластической области всегда неоднородна. Таким образом, относительный сдвиг может характеризовать только конечные деформации материала, уже прошедшего через зону стружкообразования.

Угол  между большой осью эллипса и направлением сдвига называют углом текстуры. Между углом текстуры и относительным сдвигом имеется связь [1]:

. (2.32)