6. Методы анализа взаимосвязей

Все социально-экономические явления взаимосвязаны. Связь между ними имеет причинно-следственный характер. Признаки, характеризующие причины и условия связи, называются факторными х, а признаки, которые характеризуют следствия связи, — результативными у. Между признаками х и у возникают разные по природе и характеру связи, а именно: функциональные и стохастические. При функциональной связи каждому значению признака х соответствует одно определенное значение у. Эта связь проявляется однозначно в каждом отдельном случае. При стохастической связи каждому значению признака х соответствует определенное множество значений y, образующих так называемое условное распределение. Как закон эта связь проявляется только в массе случаев и характеризуется изменением условных распределений у. Если заменить условное распределение средней величиной , то образуется разновидность стохастической связи — корреляционная. В случае корреляционной связи каждому значению признака х соответствует среднее значение результативного признака .

Примером стохастической, и в частности корреляционной, связи является распределение проданных на бирже недвижимости однокомнатных квартир по их стоимости у и размеру общей площади х (табл. 6.1).

Таблица 6.1

Размер общей площади, м2 х	Количество квартир со стоимостью тыс. усл. ден. ед.						Средняя стоимость квартиры, тыс. усл. ден. ед.
	9—11	11—13	13—15	15—17	17—19	Итого fi
До 25	26	12	2	—	—	40	10,8
25-30	4	9	12	5	—	30	13,2
30-35	—	4	6	10	4	24	15,2
35 и более	—	—	—	—	6	6	18,0
В целом	30	25	20	15	10	100	13,0

Каждой группе по факторному признаку соответствует свое распределение y, отличающееся от других групп и от безусловного итогового распределения. Следовательно, между признаками наблюдается стохастическая связь.

Условные распределения можно заменить средними значениями результативного признака, вычисляемыми как средняя арифметическая взвешенная:

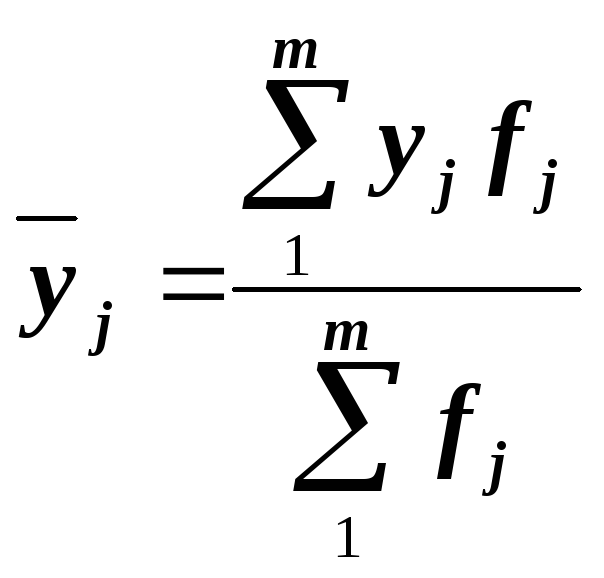
Постепенное изменение средних от одной группы к другой свидетельствует о наличии корреляционной связи между признаками.

Характеристикой корреляционной связи является линии регрессии, которая рассматривается в двух моделях: аналитической группировки и регрессионного анализа. В модели аналитической группировки — это эмпирическая линия регрессии, которая образуется из групповых средних значений результативного признака для каждого значения (интервала) х_о.

Эффекты, воздействия х на у определяются как отношение приростов средних групповых значений _y : _x, где , По данным табл. 6.1 приросты _x во всех группах одинаковы — 5 м², а средняя стоимость проданных квартир увеличивается по группам таким образом: = 13,2 - 10,8 = 2,4 тыс. усл. ден. ед.; = 2,0; = 2,8.

Следовательно, с увеличением размера общей площади квартир на 1 м² их стоимость в среднем возрастает соответственно на: : = 2,4 : 5 == 0,48; на 0,4 и 0,56 тыс. усл. ден. ед.

Оценка тесноты связи основывается на правиле сложения дисперсий. В модели аналитической группировки мерой тесноты является отношение межгрупповой дисперсии к общей, которое называют корреляционным отношением:

где ² — общая дисперсия, измеряющая вариацию результативного признака у, обусловленную влиянием всех возможных факторов; межгрупповая дисперсия ² измеряет вариацию результативного признака у за счет воздействия только группировочного признака х. Корреляционное отношение колеблется в пределах от 0 до 1 (или от 0 до 100%). При функциональной связи ² = 1, если связь отсутствует — ² = 0. Чем ближе ² к единице, тем теснее связь.

По данным табл. 6.1, общая дисперсия стоимости проданных квартир составляет

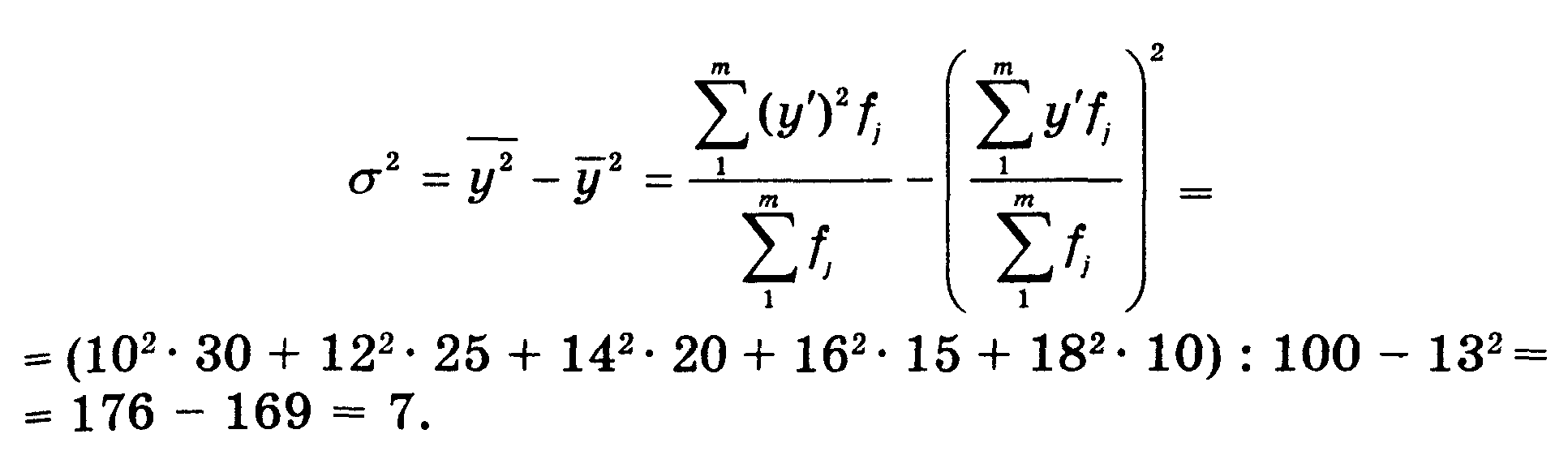
В табл. 6.2 представлена аналитическая группировка проданных квартир, описывающая зависимость их стоимости от общей площади. Там же показан расчет межгрупповой дисперсии.

Таблица 6.2

Общая площадь квартиры, м2	Количество квартир	Средняя стоимость квартиры, тыс. усл. ден. ед.
xi	fi
До 25	40	10,8	-2,2	193,6
25—30	30	13,2	0,2	1,2
30—35	24	15,2	2,2	116,2
35 и более	6	18,0	5,0	150,0
В целом	100	13,0	X	461,0

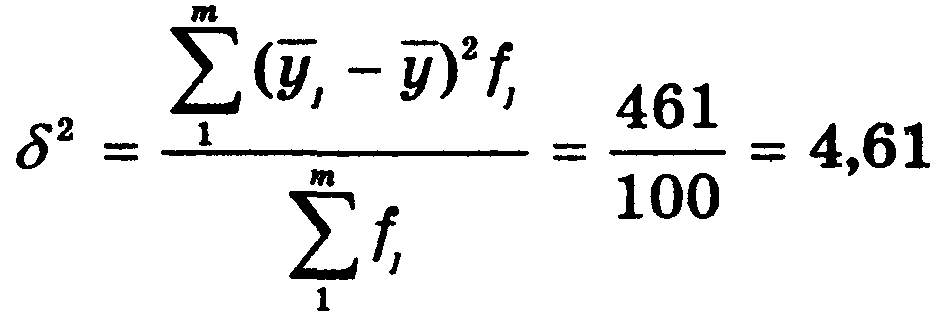
Корреляционное отношение составляет:

следовательно, вариация стоимости проданных квартир на 66% объясняется вариацией их общей площади и на 34% — вариацией других факторов. Таким образом, связь между признаками достаточно тесная.

Однако тесная связь может возникнуть случайно, поэтому необходимо проверить ее существенность, т. е. доказать неслучайность связи. Проверка существенности связи — это сопоставление фактического значения ² с его критическим значением для определенного уровня существенности а и числа степеней свободы k₁ = m - 1 и k₂ = n – m, где m — число групп; n — объем совокупности. Если , то связь признается существенной. Критические значения корреляционного отношения для а = 0,05 приведены в прил. 4.

В нашем примере k₁ = 4 - 1 == 3, k₂ = 100 - 4 == 96. Из-за отсутствия в таблице критических значений k = 96 используем ближайшее (k₂ = 100), тогда

²_0,95 (3, 100) = 0,075.

Поскольку ² 0,659 > 0,075, то связь признается существенной с вероятностью 0,95.

В модели регрессионного анализа характеристикой корреляционной связи является теоретическая линия регрессии, описываемая функцией Y = f(x), которая называется уравнением регрессии. В зависимости от характера связи используют:

линейные уравнения Y = а + bх, когда при изменении х признак у изменяется более или менее равномерно;

нелинейные уравнения, когда изменение взаимосвязанных признаков происходит неравномерно (с ускорением, замедлением или с переменным направлением связи), в частности степенное Y = ax^b, гиперболическое Y = а + b/х, параболическое Y = а + bх + сх² и т. п.

Чаще применяются линейные или приведенные к линейному виду уравнения. В линейном уравнении параметр b — коэффициент регрессии — показывает, на сколько единиц в среднем изменится у при изменении х на единицу. Он имеет единицу измерения результативного признака. При прямой связи b — величина положительная, при обратной — отрицательная. Параметр а — свободный член уравнения регрессии, т. е. это значение Y при х. == 0. Если х не принимает нулевых значений, этот параметр не имеет интерпретации. Параметры функции определяются методом наименьших квадратов, согласно которому сумма квадратов отклонений эмпирических значений у от теоретических Y минимальна: (у - Y)²  min. В соответствии с условием минимизации параметры вычисляются на основе системы нормальных уравнений:

Отсюда

Пример. Расчет параметров линейного уравнения регрессии рассмотрим на примере связи между суточной стоимостью туристических путевок в одном из турагенств и продолжительностью отдыха (дней):

Таблица 6.3

Номер путевки	Продолжи­тельность отдыха, дней	Суточная стоимость путевки, усл. ден. ед.	ху	x2	Y	(y - Y)2	y2
	x	y
1	5	78	390	25	91,6	185,0	6084
2	14	55	770	196	52,5	6,2	3025
3	7	95	665	49	82,9	146,4	9025
4	18	30	540	324	35,1	126,0	900
5	14	53	742	196	52,5	0,2	2809
6	20	26	520	400	26,4	0,2	676
7	7	85	595	49	82,9	4,4	7225
8	15	50	750	225	48,1	3,6	2 500
Итого	100	472	4972	1464	472,0	372,0	32244

Величины, на основании которых вычисляются параметры:

x = 100; y = 472; xy = 4972; x² = 1464; n = 8; = 100 : 8 = 12,5; = 472 : 8 = 59. Следовательно, параметры составляют:

а = 59 - (-4,34) - 12,5 = 113,25.

Тогда уравнение регрессии имеет вид Y = 113,25 - 4,34x, т.е. с увеличением продолжительности отдыха на один день суточная стоимость туристической путевки дешевеет в среднем на 4,34 усл. ден. ед.

Коэффициент регрессии в небольших по объему совокупностях подвержен случайным колебаниям. Поэтому необходима проверка его существенности с помощью t-критерия (Стьюдента):

где b — коэффициент регрессии; _b — стандартная ошибка, рассчитываемая по формуле

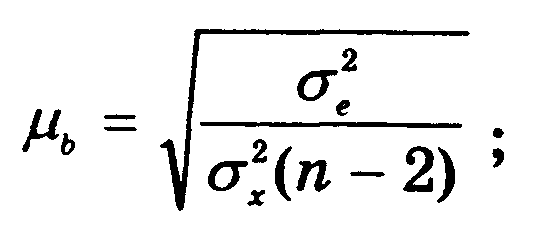
— остаточная дисперсия; — дисперсия факторного признака; n — объем совокупности.

По данным табл. 6.3 = 26,75, = 46,5, n = 8, тогда

что значительно выше критического значения t_0,95 (6) =2,54.

Следовательно, с вероятностью 0,95 влияние продолжительности отдыха на суточную стоимость путевок признается существенным. Для коэффициента регрессии также определяются доверительные границы b ± t_b. С вероятностью 0,95 доверительные границы коэффициента регрессии составляют

-4,34 ± 2,54 • 0,54, или -4,34 ± 1,37 усл. ден. ед.

Характеристикой относительного изменения у за счет х является коэффициент эластичности

который показывает, на сколько процентов в среднем изменяется результативный признак с изменением факторного на 1%. По данным табл. 6.3

следовательно, с увеличением продолжительности отдыха на 1% суточная стоимость путевок уменьшается в среднем на 0,9%.

На основании уравнения регрессии определяются теоретические значения Y, т. е. значения результативного признака при условии, что на него влияет только фактор х, а другие факторы остаются на неизменном уровне. В приведенном примере Y — это ожидаемая стоимость путевок за счет влияния только продолжительности отдыха. Так, для х = 5 дней суточная стоимость путевки составит Y = 113,25 - 4,34 • 5 = 91,6 усл. ден. ед., что несколько отклоняется от фактического значения.

Отклонения эмпирических значений у от теоретических Y называют остаточными. Они характеризуют влияние на результативный признак всех других факторов, кроме х. Средний размер этих отклонений определяет остаточная дисперсия

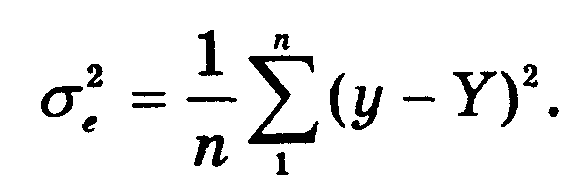
Вариацию у, обусловленную влиянием только фактора х, измеряет факторная дисперсия:

Доля факторной дисперсии в общей характеризует тесноту связи и называется коэффициентом, детерминации:

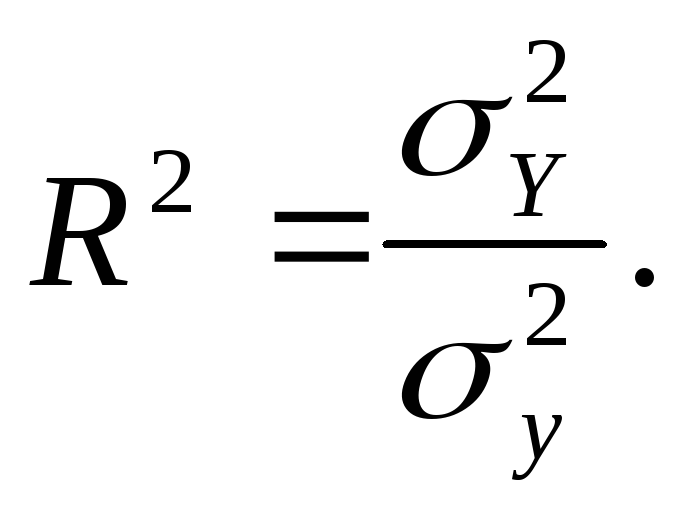
Он имеет такое же содержание, интерпретацию и цифровые границы, что и ². По данным табл. 6.3

следовательно, по правилу сложения дисперсий:

= 549,5 - 46,5 = 503,

или по другой формуле

(113,25  472 - 4,34  4972) - 59² =503

Тогда R² = 503 : 549,5 = 0,915, т.е. 91,5% вариации суточной стоимости путевок линейно связаны с вариацией продолжительности отдыха, а 8,5.% вариации приходится на остальные факторы. Следовательно, связь очень тесная.

Тесноту связи можно оценить также индексом корреляции R = , однако интерпретируется только R². Для линейной связи используется линейный коэффициент корреляции (Пирсона) r:

который принимает значения в пределах 1, поэтому характеризует не только тесноту, на и направление связи. Положительное значение свидетельствует о прямой связи, а отрицательное — об обратной. В рассмотренном примере

где . Следовательно, связь между суточной стоимостью туристических путевок и продолжительностью отдыха является тесной и обратной. Абсолютное значение r равно индексу корреляции:

Однако для интерпретации г необходимо перейти к R²= r².

Проверка существенности связи осуществляется таким же образом, как и в модели аналитической группировки, путем сравнения R² и . Отличия касаются только определения k₁ и k₂ в которых m — число параметров уравнения регрессии. В нашем примере k₁ =2 – 1 = 1, а k₂ = 8 – 2 = 6, критическое значение R²_0,95(1,6) = 0,500 значительно меньше фактического R² = 0,915.

Пример. По данным табл. 6.4 оценим тесноту связи между уровнем эффективности экономики и надежностью делового партнерства для семи стран Восточной Европы. Поскольку информация представлена в форме интегральных показателей (оценки в баллах), необходимо провести ранжирование стран. Наименьшему значению интегрального показателя придается ранг 1, наибольшему — ранг 7. Сумма квадратов отклонений рангов составляет

а коэффициент ранговой корреляции

Значение коэффициента ранговой корреляции свидетельствует о наличии прямой и достаточно заветной связи между указанными параметрами риска иностранного инвестирования экономики. По прил. 6 критическое значение коэффициента ранговой коррекции для а = 0-05 и n = 7 составляет _0,95(7) = 0,71, что значительно меньше фактического. Следовательно, существенность связи доказана с вероятностью 0,95.

Таблица 6.4

Страна	Интегральные показатели		Ранги показателей		Отклоне­ние рангов dj
	эффективности экономики (max = 10)	надежности делового партнерства (max = 100)	Rx	Ry		d2j
А	5,9	54.9	6	7	-1	1
В	7,1	54,8	7	6	1	1
С	4,2	45,3	4	5	-1	1
D	3,4	36,9	3	4	-1	1
К	4,9	35,8	5	3	2	4
М	2,7	26,4	1	2	-1	1
Р	2,9	24,8	2	1	1	1
Итого	X	X	X	X	0	10

Анализ взаимосвязей между атрибутивными признаками проводится на основе таблиц взаимной сопряженности (взаимозависимости), описывающих комбинационные распределения совокупностей по двум признакам — факторному х и результативному у. При наличии стохастической связи условные распределения изменяются от группы к группе. Оценка тесноты стохастической связи основывается на отклонениях частот (частостей) условных распределений от безусловного, т.е. на отклонениях фактических частот f_ij от теоретических F_ij, пропорциональных итоговым частотам безусловного распределения:

где f_i0 — итоговые частоты по признаку х; f_0j — итоговые частоты по признаку у, n — объем совокупности.

Очевидно, что

Абсолютную величину отклонений (f_ij - F_ij) характеризует квадратическая сопряженность Пирсона ²:

Если стохастическая связь отсутствует, то ² = 0. Для того, итобы сделать вывод о существенности связи, необходимо сравнить фактическое значение ² с критическим для заданной вероятности 1 -  и числа степеней свободы k = (m_x — 1)(m_y - 1), где m_x и m_y — соответственно количество групп по признакам х и у. Критические значения ² приведены в прил. 3.

Относительной мерой тесноты стохастической связи служат коэффициенты взаимной сопряженности С, которые по содержанию идентичны коэффициентам корреляции. Если m_x = m_y, используют коэффициент сопряженности Чупрова:

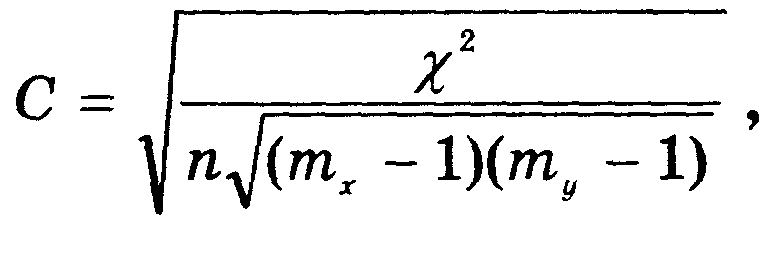
если m_x  m_y, предпочтение отдают коэффициенту сопряженности Крамера:

где m_min — минимальное количество групп по признаку х или у.

Значения коэффициента С колеблются в пределах от 0 до 1.

Пример. В табл. 6.5 приведено комбинационное распределение респондентов как потенциальных инвесторов по возрасту и склонности к риску. К группе рискующих отнесены респонденты, имеющие намерение приобрести ценные бумаги, несмотря на риск, осторожные не рискуют без гарантий, нерискующие избегают риска вообще. Концентрация частот около диагонали из верхнего левого угла в правый нижний свидетельствует о наличии стохастической связи. Фактическое значение ² составляет

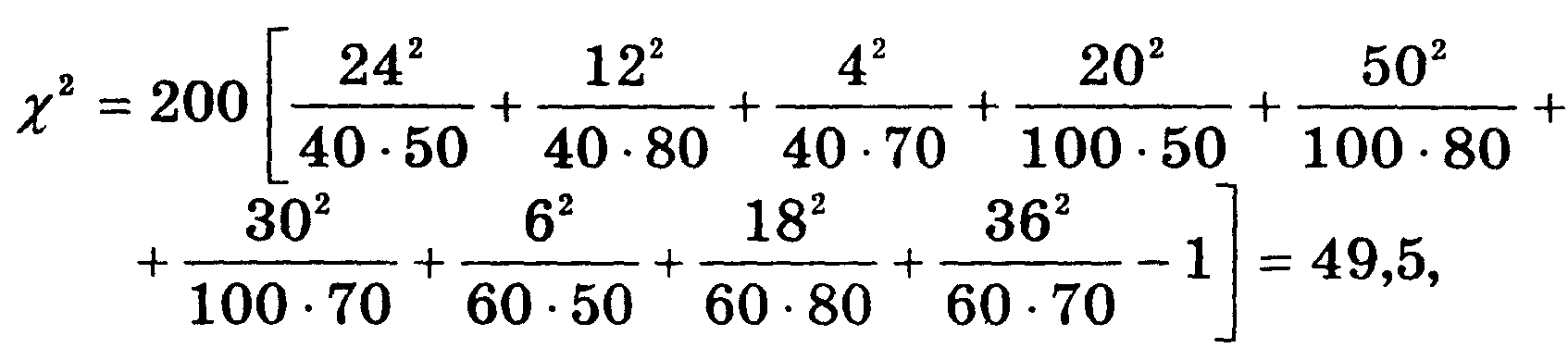
что значительно выше критического ²_0,95 (4) = 9,49. Следовательно, существенность связи между возрастом респондентов и склонностью их к риску доказана с вероятностью 0,95.

Таблица 6.5

Возраст, лет	Тип инвестора			Итого
	рискующий	осторожный	нерискующий
До 30	24	12	4	40
30—50	20	50	30	100
50 и старше	6	18	36	60
Итого	50	80	70	200

Поскольку m_x = m_y =3, для оценки тесноты связи используем коэффициент взаимной сопряженности Чупрова:

т.е. связь между признаками умеренная.

В случае, когда m_x = m_y = 2, расчет коэффициента взаимной сопряженности упрощается:

В статистической литературе коэффициент С для 4-клеточной таблицы называют коэффициентом контингенции (ассоциации). Очевидно, что ₂ = nС².

Для анализа таблиц такого типа используют также отношение перекрестных произведений, или отношение шансов:

Отношение шансов характеризует меру относительного риска (выигрыша), связанного с фактором х.

Пример. По данным табл. 6.6 оценим тесноту связи между восприятием рекламы и приобретением рекламируемого товара, а также результативность рекламы.

Восприятие рекламы	Количество респондентов		Итого
	приобрели товар	не приобрели товар
Запомнили рекламу	9	31	40
Не запомнили рекламу	2	38	40
Итого	11	69	80

Таблица 6.6

Коэффициент контингенции свидетельствует о наличии стохастической связи

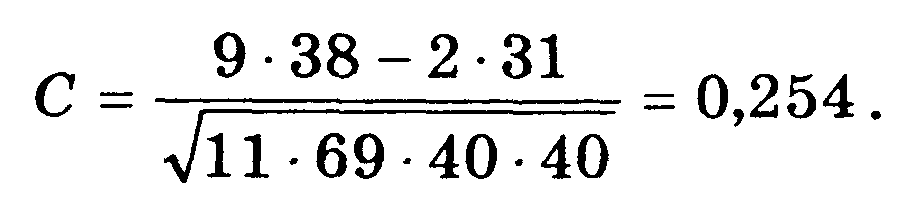
фактическое значение ² = nС² = 80 • 0,2542 = 5,16, что выше критического значения ²_0,95(1) = 3,84. Следовательно, существенность связи доказана.

Отношение шансов составляет

т.е. шансы реализовать рекламируемый товар в 5,5 рааза выше по сравнению с нерекламируемым.

Методы анализа таблиц взаимной сопряженности можно использовать и для количественных признаков (см., например, комбинационное распределение табл. 6.1), однако следует отметить, что меры тесноты корреляционной связи – коэффициент детерминации и корреляционное отношение – более чувствительны.