Вопрос 13

Существование односторонних пределов у монотонных функций.

Def.: Функция называется возрастающей (убывающей) на если из следует (или наоборот).

Th.: Пусть функция f возрастает на (a,b).Тогда

Pr.: Пусть Возьмем произвольное Выберем таким, что . Тогда в силу возрастания функции f, Следовательно,

Вопрос 14

Непрерывность функций в точке. Непрерывность сложной функции.

Def.: Функция f называется непрерывной в точке , если выполняется какое-либо из следующих условий:

1. ;

2. ;

3. для

4. для

5. для

6. для

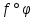Th.: Пусть f непрерывна в точке непрерывна в точке Тогда непрерывна в точке .

Pr.: Пусть – произвольная окрестность 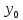. В силу непрерывности f в . В силу непрерывности в точке . Последнее означает, в частности, что определена на и значения ее в точках лежат в . Следовательно, на определена сложная функция , причем . Где . В силу произвольности это означает непрерывность в точке .

Вопрос 16

Достижимость (точной) верхней и (точной) нижней грани функцией, непрерывной на отрезке.

Th.: Теорема Вейерштрасса. Функция, непрерывная на отрезке, ограничена и достигает своих верхней и нижней грани.

Pr.: Пусть 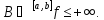По определению верхней грани . Следовательно, Последовательность ограничена, так как По теореме Б.-В. Выделим из нее сходящуюся подпоследовательность при Переходя к пределу в неравенстве , получаем, что В силу непрерывности функции f в точке 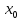имеем

С другой стороны – последовательность сходящейся к В последовательности. Поэтому Из последних двух соотношений получаем, что ( Отсюда следует, во-первых, что т.е. что функция f ограничена сверху, и, во-вторых, что функция f достигает своей верхней грани в точке Теорема доказана.

Вопрос 17

Теорема о промежуточных значениях непрерывность функции.

Th.: Теорема Больцано-Коши. Пусть функция непрерывна на отрезке [a,b], f(a)=A, f(b)=B. Пусть С находится между А и В. Тогда .

Pr.: Пусть для определенности, A=f(a)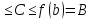. Поделим отрезок [a,b] пополам и через обозначим такую его половину, для которой fПоделим отрезок пополам и через его половину, для которой f. Продолжая процесс, получим стягивающуюся систему вложенных отрезков , для которых f.

Пусть Тогда при и в силу непрерывности функции f в точке 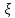. при Переходя к пределу в последнем неравенстве, получаем . Теорема доказана.

Вопрос 18

Теорема о обратной функции.

Th.: Пусть функция задана на отрезке [a,b], строго возрастает и непрерывна. Тогда функция задана на отрезке 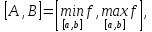строго возрастает и непрерывна.

Pr.: Найдем область значений Поскольку то . С другой стороны, по теореме Б.-К. для так что [A,B]. Следовательно,

Строгое возрастание следует из леммы (функция от f также строго монотонна, как f в степени).

Установим непрерывность . Пусть сначала так что Пусть столь мало, что

Функция f устанавливает взаимно однозначное соответствие отрезка и отрезка . При этом . Возьмем столь малым, что ( Тогда Следовательно, непрерывна в точке .

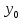Пусть теперь Тогда непрерывность в точке доказывается аналогично. Теорема доказана.