Вопрос 5

Свойства пределов, связанные с неравенствами.

Def.: Последователоьность 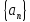называется ограниченной сверху или снизу, если множество значений ее элементов ограничено сверху или снизу.

Def.: Последовательность называется ограниченной сверху или снизу если . Два приведенных определния эквивалентны.

Вопрос 6

Арифметические операции со сходящимися последовательностями.

L.: Сумма, разность и произведение бесконечно малых последовательностей являются бесконечно малыми последовательностями.

Вопрос 7

Теорема о пределе ограниченной монотонной последовательности.

Th.: Всякая возрастающая последовательность имеет предел в Этот предел конечен (т. е. является числом), если последовательность ограничена сверху, и равен , если последовательность не ограничена сверху.

Pr.: Пусть a: Тогда, по определению верхней грани, и для . Поскольку при , получаем, что . Это означает, что , что и требовалось доказать.

Вопрос 8

Теорема Кантера о вложенных отрезках.

Th.: Множество всех точек отрезка [0,1] несчетно.

Pr.: Допустим противное. Тогда все точки отрезка [0,1] можно занумеровать: Поделим отрезок [0,1] на три ровных отрезка и обозначим через один из них, свободный от точки . на три равных отрезка и обозначим через один из них, свободный от точки . Продолжая процесс, получим систему вложенных отрезков . По теореме о вложенных отрезках существует точка c, принадлежащая всем отрезкам системы. Эта точка c не совпадает ни с одной из занумерованных точек 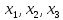… , так как произвольная из них не содержится в отрезке , в то время как с содержится в этом отрезке. Допуская, что все точки отрезка [0,1] занумерованы, мы пришли к противоречию, найдя точку , отличную от занумерованных. Это противоречит нашему предположению. Теорема доказана.

Вопрос 9

Подпоследовательности и частичные пределы. Два определения частичного предела, их эквивалентность. Верхний и нижний пределы последовательностей.

Def.:Частичным пределом последовательности называется предел какой-либо ее подпоследовательности, сходящейся в .

Def.:Частичным пределом последовательности называется элемент , любая окрестность которого содержит бесконечное число элементов последовательности.

Pr.: Эквивалентности 2х определений. Покажем сначала, что из определения 1 следует определение 2. Покажем сначала, что из определения 1 следует определение 2. Пусть является частичным пределом в смысле определения 1. Тогда, по определению предела, в любой содержатся почти все элементы некоторой подпоследовательности. Следовательно, удовлетворяют определения подпоследовательности.

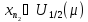Теперь докажем обратное. Пусть является частичным пределом в смысле определения 2. Выберем какой-либо элемент последовательности , затем выберем какой-либо элемент последовательности , удовлетворяющий условию . Это возможно, так как содержит бесконечное число элементов. Выберем затем, . Продолжая процесс, получим подпоследовательность , сходящуюся в , так как при 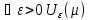содержит все ее члены, начиная с члена с номером , где .

Def.: Верхним (нижним) пределом последовательности называется наибольший (наименьший) в из ее частичных пределов. Обозначается как .