Вопрос 10
Теорема Больцано-Вейерштрасса.
Th.: Всякая ограниченная последовательность имеет хотя бы один частичный предел.
Другая формулировка: Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Pr.:
Пусть
– произвольная последовательность.
.
-
Это значит, что
содержит почти все элементы
последовательности, т. е.
.
Следовательно
- единственный частичный предел
,
так что
-
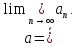
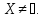Тогда
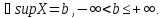Покажем, что b
.
Возьмем произвольное
,
и пусть
.
Тогда из определения верхней грани
следует, что найдется
Поэтому правее
лежит
бесконечное число элементов
последовательности
.
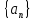Если
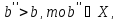так что правее
- не более конечного числа элементов
последовательности. Следовательно
содержит бесконечное число элементов
последовательности
и, в силу произвольности
– частичный предел
.
Остается показать,
что b
– наибольший частичный предел
,
т.е. b
.
Допуская противное, предполодим, что
существует частичный предел
Тогда всякая окрестность
содержит бесконечно много элементов
последовательности. Но это противоречит
тому, что при b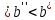
правее
- не более конечного числа последовательности.
Следовательно, b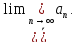
Вопрос 11
Критерий Коши сходимости числовой последовательности.
Def.:
Последовательность
называется фундаментальной, если для
нее выполнено условие Коши:
.
Th.: Для сходимости последовательности необходимо и достаточно, чтобы она была фундаментальной.
Pr.:
Необходимость. Пусть последовательность
сходится и
.
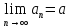Возьмем произвольное
.
Если теперь
,
то
что и требовалось доказать.
Достаточность:
Пусть последовательность
фундаментальна, т.е. удовлетворяют
условию определения. Докажем ее
сходимость. Покажем, что последжовательность
ограничена. Возьмем
Тогда из условия определения следует:
.
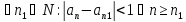Так что,
Следовательно
– ограничена. По теореме Б.-В., из
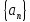можно выделить сходящуюся
подпоследовательность
Пусть
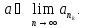Покажем, что а является пределом
.
Пусть
.
Тогда
.
Переходя в этом неравенстве к пределу
при
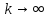получаем, что
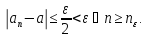В силу произвольности
это означает, что
.
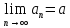Вопрос 12
Определение предела функции в точке в терминах окрестностей и в терминах последовательностей (по Коши, Гейне), их эквивалентность.
Def.:
Пусть функция f
определена на
называется пределом функции f
при
если
при
.
Def.:
По Гейне. Пусть функция f
определена на
называется пределом функции f
при
если
Def.:
По Коши. Пусть функция f
определена на
называется пределом функции f
при
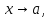если
Def.:
Пусть функция f
определена на
.
Точка
называется пределом f
при
,
если
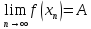для
любой последовательности
Th.: Определения эквивалентны.
Pr.:
Покажем сначала, что 1
.
Пусть последовательность
в смысле определения 1. Пусть
последовательность
Покажем, что
.
Возьмем
произвольное
.
Тогда в силу определения 1
.
В силу сходимости
для нашего
.
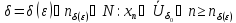Но тогда
,
т.е.
,
что и требовалось показать.
Докажем
обратное.
В качестве
и соответствующее значение x
обозначать через
,
т.е. при
.
Но это означает, что
для последовательности {
имеем
.
А не является пределом f(x)
при
в смысле определения 2, что противоречит
условию. Утв.доказано.